SCILABによる制御系設計 その12

Scilab 12
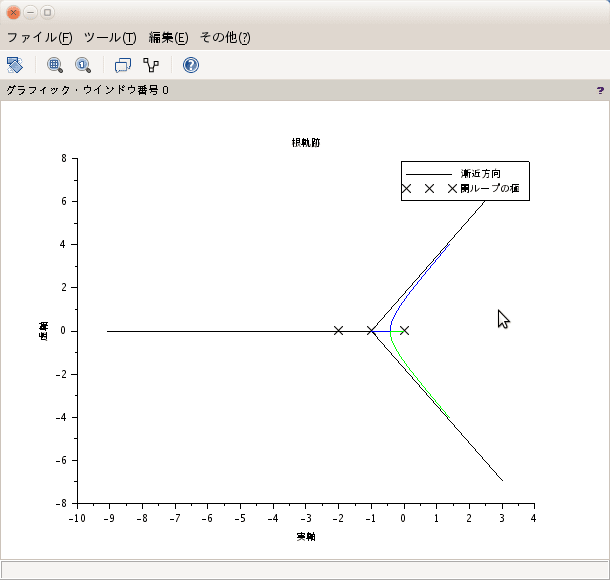
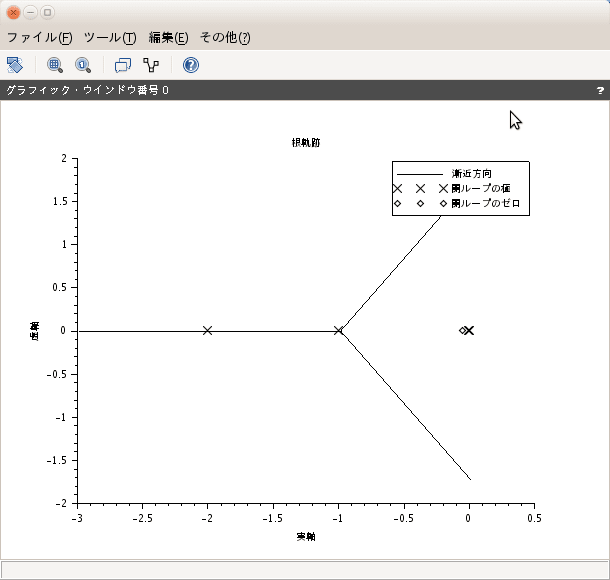
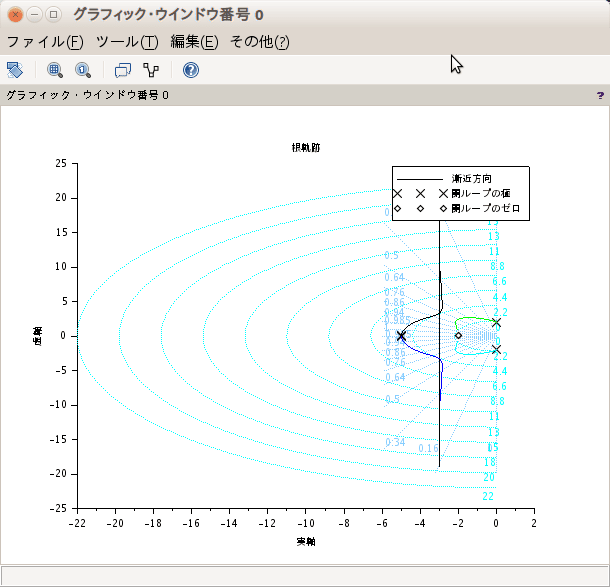
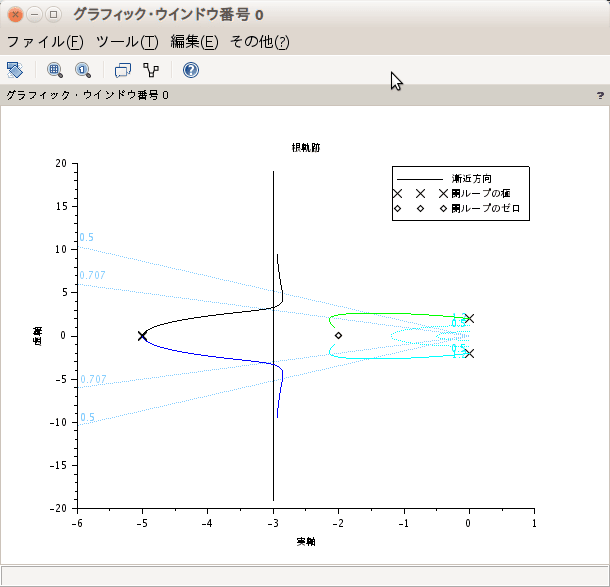
前回までで根軌跡は終了。scilabで使ってきたevansという関数であるが、これはEvansが根軌跡法を提案したのでそれを使っているのであろう。今回から、周波数応答法に入る。ところがEvansが提案した根軌跡法の方が新しいらしい。周波数応答で出てくるbode線図やNyquist線図の方が古い。
ということで、周波数応答に入ろう。
尾形先生の本では第５章　周波数応答解析　である。
応答というのであるから、入力があって、それに対する応答をみるということである。システムの応答は、その応答の大きさと追従性つまり位相で評価できる。入力に対して、応答の大きさをゲインという。一方位相は、入力が振動であれば、その振動数に対してどの程度の位相ずれがあるかということで、追従性を評価する。低い周波数で振動させた場合、例えばロボットの腕などの動きは、多分追従して、入力どおりの大きさと、同位相で動く。ところが、高い周波数で振動させた時には、その応答はだんだん遅れて動き、さらに動きの大きさも小さくなってしまうであろう。
これらのゲインと位相を図で書いたものが、ボード線図である。
さっそく、bode線図について書いてみよう。
-->s=poly(0,'s');
-->ht=25/(s^2+4*s+25);
-->H=syslin('c',ht);
-->bode(H);



となり、尾形先生の例題５−１と一致する。上段のグラフがゲインで下段が位相を示す。厳密には、MATLABは横軸がｒａｄ／ｓであるのに対してscilabはHzである。どちらが良いのか一長一短であるが。
さて、このシステムは伝達関数で１入力１出力なので応答は一つであるが、多入力である場合にはどうなるか、やってみよう。MATLABであれば、例えば２入力、２出力であれば４組のボード線図がそのまま書かれる。
さて、
->A=[0 1;-25 -4];
-->B=[1 1;0 1];
-->C=[1 0;0 1];
-->H=syslin('c',A,B,C);
-->bode(H);
!--error 95
引数 1 の型が間違っています: SISO を指定してください.
at line 91 of function repfreq called by :
at line 41 of function bode called by :
やっぱだめだ、SISO　つまり１入力１出力しか受け付けない。
分解して、表示するしかなさそうですね。
今回はここまで。

SCILABによる制御系設計 その11

Scilab 11
さてさて、専門的なブログとなっていますが、皆さん理解していますか？
実は、私もあやしいです。
そもそも、複素平面　って　何？
ということや
ラプラス変換　演算子　など　？？？？？　かもしれません。
イメージしやすい例題で解説しても良いのですが、とりあえずscilabの使い方
という視点でやっています。
前回まで、伝達関数表現の　極配置　について見てきました。尾形先生の教科書ではこの後、４−３で「根軌跡上の任意の点に対応するゲインKの値を探索する」、４−４「非最小位相系の根軌跡」４−５「条件安定システムの根軌跡」４−６「むだ時間があるシステムの根軌跡」と続きます。
探した限り、matlabであるrlocusに対応したのがscilabでの対応が難しいため（やろうと思えばやれますが。。。）
ここらへんは飛ばします。（おまえわかってないから飛ばすのか！　という声が聞こえますが）
で、根軌跡によって　当ブログの本題の制御系の設計をやってみましょう。
つまり参考書は４−７「制御システムの性能を補償するための根軌跡によるアプローチ」です。
制御システムは　このやり方は１）モデルが与えられている　そして　２）根軌跡がわかるので　３）補償する制御器を与えてやり　４）MATLABやscilabで評価してやる。
ということになります。　具体的に例題で見ていきましょう。
４−７−１　として　根軌跡による　位相進み補償がまず最初です。。。
zzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz
寝てますね
あきらめましょう
結局、設計は位相進み補償、位相進み遅れ補償、などを机上でやり
ステップ応答で比較しているのに上記４）をやっているということです。
例題４−１３の結果を示して今回は終わりにします。すみません
s=poly(0,'s');
-->Ht=1.06/(s*(s+1)*(s+2));
-->H=syslin('c',Ht);
-->evans(H,100);
として、まずHtという補償前の前向き伝達関数を与えてその根軌跡を見る。
すると



こんな感じの根軌跡が得られる。
補償器を設計して（設計は尾形先生の本に譲る）
->Gt=0.9656*(s+0.05)/(s+0.005);
これが補償器
-->GH=Gt*Ht;
直列にして
-->G=syslin('c',GH);
-->clf()
-->evans(G,100);
警告: evans: 曲線は最初の 2000 個の離散点に丸められています。
あれ　まあ良いか


となり補償後のものが得られました。この評価は、ステップ応答の比較をしてみると


あらら　何かおかしい
今回はここまで　修正してまたアップします。

SCILABによる制御系設計 その１０

Scilab 10
根軌跡の続き
Ht=(s+2)^2/(s^2+4)/(s+5)^2;
-->H=syslin('c',Ht);
-->evans(H,100);
-->sgrid
とすることで　このような極座標グリッド線が入ったグラフがかける
これはMATLABとほぼ同じ
ただし、デフォルトの色がなあ　ちょっと見にくい


尾形先生のprogram４−１０などにより、減衰ζ=0.5 と0.707の放射線と
ω=0.5、1,2のみの円を示したれば

>sgrid([0.5,0.707],[0.5,1.2]);
でこうなる。
ζ：減衰は複素平面上で角度φの角度を持った放射線になる。またωは一定半径の円となります。


ちょっといびつ

SCILABによる制御系設計 その８

Scilab8
３　過渡応答解析 （その5）

初期条件を与えた場合の応答

-->t=0:0.05:10;

-->A=[0 1 0;0 0 1;-10 -17 -8];

-->B=[0;0;0];

-->C=[1 0 0];

-->D=[0];

状態空間表現で

-->x0=[2;1;0.5];

初期状態ベクトルをこのようにする

-->E=[1 0 0;0 1 0;0 0 1];
これをいつも忘れる

-->u=zeros(1,201);
入力はなし

-->plot2d(csim(u,t,des2ss(A,B,C,D,E),x0));
警告: csim: 入力引数 #1 は連続時間系で指定してください.

ということで


となる
尾形先生のprogram 3-36参照
matlabではinitialというコマンドを使うが
scilabでは一貫してcsimでいける


さらに過渡応答のところで　例題３−２５では３次元プロットをしている。
例えばscilabでは
減衰を６種類変えて　３次元のプロットは。
matlabだとmeshというのでいけるのですが
scilabは　例えば次のようにしました

>for n=1:6
-->sy=1/(s^2+2*(n-1)*0.2*s+1);
-->y(n,:)=csim('step',t,tf2ss(sy));
-->end

->nn=[1 2 3 4 5 6];
-->plot3d(nn',t',y);
で

ちょっと色がきたないかな

SCILABによる制御系設計 その7

Scilab7
３　過渡応答解析 （その4）

インパルス応答をやってみよう

plot2d([t',t'],[(csim('impulse',t,des2ss(A,B,C,D,E)))',0*t'])

でいけるはず。

-->A=[0 1;-1 -1];

-->B=[0;1];

-->C=[1 0];

-->D=[0];

-->E=[1 0;0 1];

-->t=0:0.01:10;

-->plot2d([t',t'],[(csim('impuls',t,des2ss(A,B,C,D,E)))',0*t'])
警告: csim: 入力引数 #1 は連続時間系で指定してください.

で


任意の入力の場合、


s=poly(0,'s');

-->sy=5/(s^2+s+5);

として

-→u=2+t;

つまりランプ入力

plot2d(csim(u,t,tf2ss(sy)));

とすれば任意の入力uに対する応答が得られる。