エンケラドゥスの海洋循環と氷と海洋の相互作用に対する塩分濃度の影響
2023年 6月 14日に提出
概要
観測データは、エンケラドゥスの氷の殻が赤道でより厚いことを示唆しています
これは、赤道から極への氷の流れを示しています。 氷の殻が平衡状態にある場合、氷の流れの物質輸送は、凍結と氷の変化によってバランスがとれなければなりません。
氷の殻の融解は、海洋の熱輸送によって調節されます。
私たちは数値海洋モデルを使用して、氷と海洋の相互作用と海洋循環を研究します。
塩分濃度が異なるエンケラドス。 塩分が根本的に決定することがわかりました
海洋の成層。 塩分濃度の低い海では層状の層が形成され、海洋に影響を与えます。
海洋循環と熱輸送。 しかし、氷の潮汐加熱がなければ、
シェルの場合、海洋の熱輸送は常に赤道方向であることが判明し、その結果凍結が起こります。
極点では氷が溶け、低緯度では氷の殻の形状を維持できなくなります。
赤道から極地までの氷の流れに逆らって。 シミュレーション結果は、氷が
エンケラドゥスの殻が平衡状態にない、または氷殻内の潮汐散逸が
氷の殻の形状を維持する上で重要です。
キーワード: エンケラドゥス – 塩分 – 成層層 – 海洋熱輸送 – 氷の形状
1. はじめに
エンケラドゥスには、全球規模の氷の殻の下に深さ約40kmの海があると考えられています。
(例、Postberg et al. 2011; Patthoff & Kattenhorn 2011; Thomas et al. 2016)。 エネルギー源
衛星全体の液体の海洋と南極地域での約10GWの熱損失を維持している
(Spencer et al. 2006; Howett et al. 2011; Spencer et al. 2013) は主に潮汐に由来すると考えられています。
散逸。 一般に、潮汐の消散は、氷の殻、海洋、および海域で起こると予想されます。
しっかりとしたコア。 海洋の潮汐加熱は、海洋の潮汐加熱に比べて無視できると考えられてきました。
氷の殻と内部の固体コア (例、Chen & Nimmo 2011; Tyler 2011; Chen et al. 2014; Beuthe
2016年; ヘイ&マツヤマ 2017; 松山ほか 2018年; ヘイ&マツヤマ 2019)。 最近ではありますが
研究は、共鳴が発生した場合、内部潮汐の消散が層状海洋でより多くの熱を生成する可能性があることを示唆しています
発生する(Rovira-Navarro et al. 2023)、エンケラドゥスの海洋の層状化(例、Kang et al. 2022b)
熱損失に匹敵する熱生成率をサポートできるほど強力である可能性は低い
レート。 氷殻内での潮汐散逸と、導管内での水の乱流散逸
南極 (Kite & Rubin 2016) は O(10 GW) に達する可能性があると主張されています (Beuthe 2019;Souˇcek et al. 2019)。
しかし、エンケラドゥスの氷のレオロジーはほとんど理解されていない。
氷殻内の潮汐散逸速度に影響を与えます。 エンケラドゥスの密度が低いことは、コアが
は多孔質であり、これがおそらくコア内での強力な潮汐散逸をサポートしており、O(10 GW)に達します(Iess et al.
2014年; ロバーツ 2015; カデックら。 〜 2016年; ショブレットら。 2017)。 解放は次の原因となるとも主張されている
海洋における散逸加熱は最大 O(0.1 GW) (Lemasquerier et al. 2017; Wilson & Kerswell)
2018年; レキエルら。 2019年; ソーダーランドら。 2020年)。 潮汐加熱の一部は
固体コアと氷の殻は依然として非常に不確実であり、底部の固体コアからのいくらかの加熱は、
それがエンケラドゥスの海洋循環を根本的に形作ると予想されています。
エンケラドゥスの氷の殻の厚さは平均約 20 km で、平らではありません。最も厚いのは、
赤道(30km以上)で最も薄いのは南極地域(10km未満)です。 もあります。
氷の殻の半球間非対称性。氷は北極よりも南極の方が薄い。
ポール (Beuthe et al. 2016; Cadek et al. ˇ 2019; Hemingway & Mittal 2019)。 顕著な勾配
氷の殻の厚さは、赤道から極への氷の流れを示唆しています。 エンケラドゥスの氷殻が
平衡状態では、氷の流れの赤道から極への物質移動は、氷の凍結によってバランスが保たれなければなりません
赤道で、極で溶けます。 氷殻モデルは一般に、凍結/融解を予測します。
エンケラドゥスでは、赤道から極地までの氷の流れのバランスをとるために、年間数ミリメートルの速度2が必要です。
または同等の、O(0.01 W /m^2) 潜熱 (Cadek et al. ˇ 2019; Kang & Flierl 2020; Kang et al. ˇ 2019; Kang et al.2022b)。
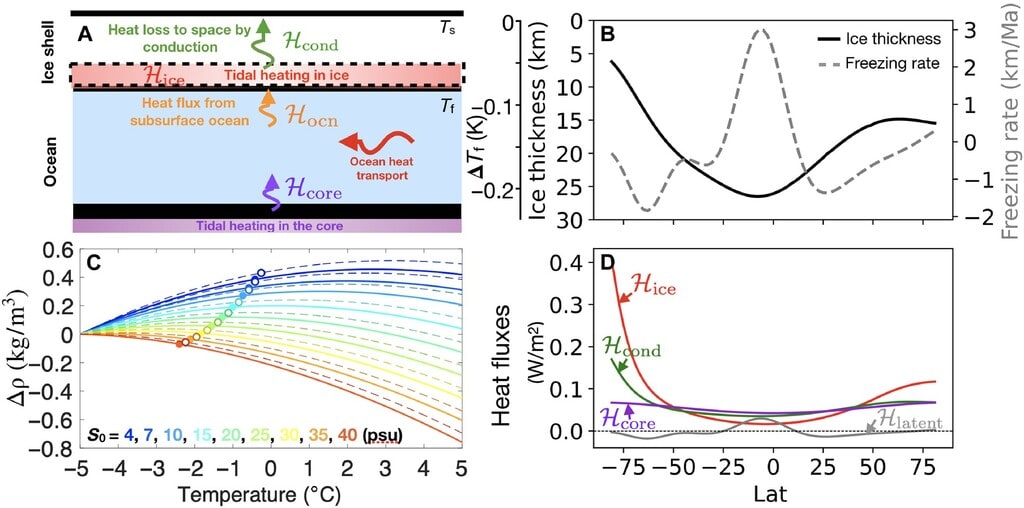
氷の凍結と融解は、熱収支、つまり関連する潜熱 (QLH、融解を正として定義) は、熱伝導性熱損失間の不均衡と一致する必要があります。
氷殻の底部 (Qcond) と海洋から氷への熱流束 (Qoi): Qcond + QLH = Qoi。
氷と海の境界面での伝導熱流束は、次のように氷の殻の厚さによって調整されます。
氷殻(Qi)内の潮汐加熱も同様です。 氷殻内で強く局所的な潮汐加熱がなければ、
氷が最も薄い極地では伝導熱損失が最も大きく、氷の凍結が促進されます。
極では、氷の形状を維持するために必要なことの逆です。 潮の干満
氷の殻は極地で最も強く、増幅されるため、この問題に対する可能な答えである可能性があります。
氷が薄い場合 (例: Beuthe 2018、2019; Kang & Flierl 2020)、したがって潜在的に
極での溶解用。 あるいは、海洋からの熱流束 Qoi は、
ポール。 氷への全球の海洋熱流束は、底部固体コアの潮汐加熱から来ます。
ピークは極点にありますが (Choblet et al. 2017)、その空間パターンは海洋循環によって調整されます。
これがこの文書の焦点です。
これまでの研究では、エンケラドゥスや他の氷の衛星における全球規模の海洋循環が調査されてきました。
(Soderlund et al. 2014; Travis & Schubert 2015; Soderlund 2019; Amit et al. 2020; Lobo et al. 2020;
カンら。 2020年; ゼン&ヤンセン 2021; アシュケナージ&ツィペルマン 2021; ビレら。 2022年; クヴォルカ&
カデック 〜 2022; カン 2022; カン&ジャンセン 2022; カンら。 2022a、b; ジャンセンら。 2023年)。 これらの研究
さまざまな方法(概念モデル、海洋のみの数値シミュレーション、
氷と海洋を組み合わせた数値シミュレーションなど)を、2 次元または 3 次元の領域で、幅広い範囲で実行できます。
パラメータとさまざまな境界条件。 ただし、3 次元のグローバル ドメインで完全に結合した氷海洋熱力学を使用したシミュレーションはまだ行われていません。 公開されているシミュレーション結果
おそらく大規模な影響の結果として、海洋循環と海洋氷の熱流束が大きく異なります。
外部パラメータの不確実性と、地球規模の海洋を現実的にモデル化することの難しさ
パラメータ体制。 したがって、エンケラドゥスの海洋循環と熱輸送の実際の体制
は不確実なままです。
海洋循環と熱輸送を決定する重要な要素の 1 つは塩分 (S) です。 塩分濃度
水の状態方程式を決定し、海洋の成層と循環に影響を与えます。 多くの
重要なのは、塩分濃度が臨界値よりも低い場合、熱膨張率 (α ≡ −(1/ρ)(∂ρ/∂T)
ここで、ρ は密度、T は温度です) は凝固点付近では負になります。 結果として、このような低水準では、
塩分の多い海洋では、海底加熱により安定した成層層が海洋上部に形成されます(Melosh et al.2004年; ゼン&ヤンセン 2021)。 負の熱膨張率が存在するためのしきい値。
負の熱膨張率が存在するためのしきい値。
エンケラドゥスの海の圧力は約20 g /kg(Zeng & Jansen 2021; Kang et al. 2022b)。
観察に基づいて、エンケラドゥスの海の塩分を推定するにはさまざまな方法があります。
塩分が豊富な氷粒の存在(Postberg et al. 2009)、シリカナノ粒子の存在(Hsu et al. 2015)、
氷導管内の沸騰水のモデルを使用 (Ingersoll & 中島 2016)、平衡水岩
相互作用 (Zolotov 2007)、海洋地球化学 (Glein et al. 2018)、および海洋熱輸送 (Kang他。 2022b)。
推定値は研究ごとに異なり、2 ~ 40 g /kg の広い範囲が与えられます。
。 したがって、両方とも「高塩分」(S > 20 g /kg)および「低塩分」(S < 20 g /kg) シナリオは慎重に行う必要があります
エンケラドゥスの海洋循環を研究するときに考慮されました。
塩分濃度は、表面密度のコントラストによって引き起こされる逆転循環にも影響を与える可能性があります。
海洋の熱輸送を調整し、氷の形状にさらに影響を与えます。 カンら。 (2022b)
規定の氷の厚さで海洋循環をモデル化し、極での融解速度を規定し、
氷の厚さによって引き起こされる推定氷の流れのバランスをとるために必要な、赤道での凍結速度
勾配。 彼らは、赤道と極の間の表面密度のコントラストが影響を及ぼしていることを発見しました。
各半球の循環を覆す。 循環の方向は平均値に依存します
海洋の塩分濃度は高いが、海洋の熱輸送は常に赤道方向であることがわかっている。
極点(氷が薄いため圧力が低い)の凝固点は赤道よりも高い
(氷が厚いため圧力が高くなります)、熱輸送は常に暖かい極から行われます。
寒い赤道へ。 赤道方向の海洋熱輸送は、極点での凍結と融解を促進します。
赤道にあるため、赤道から極までの氷殻の厚さの勾配を減少させるように作用します。
アイスポンプ効果として知られています (Lewis & Perkin 1986)。
氷の殻と底部の固体コアの間の潮汐加熱の分配も影響を与える可能性があります。
海洋の熱輸送は、2 つの半球間の非対称な氷殻の形状にさらに影響を与えます。
カンら。 (2022a) 氷がわずかに存在する半球間の非対称性を持つ氷の幾何学形状を規定する
南半球ではさらに薄い。 完全に結合した氷海の熱力学を組み込んでいます。
氷の殻と底部の固体コアの両方で潮汐散逸を伴う 2 次元ドメイン。 彼らがそれを発見したのは、
加熱は氷殻内の潮汐散逸によって支配され、南ではより強い融解が起こる
北よりも極に位置し、逆転した循環により熱が南に運ばれ、熱が増加します。
非対称性。 代わりに、加熱が主に中心部で行われる場合、中心部での凍結がより強くなります。
南極は北極よりも高く、転倒によって熱が北に運ばれるため、
非対称。
今回我々は、海洋熱輸送に焦点を当て、エンケラドゥスにおける海洋循環と氷海洋相互作用に対する塩分濃度の影響を研究する。 私たちは、
マサチューセッツ工科大学の全身循環モデル (MITgcm) (Adcroft et al. 2018)、
所定の氷の形状と完全に結合した氷と海の熱力学を備えています。 潮汐加熱を除く
固体コアからの海洋熱輸送が氷の中で維持できるかどうかに特に焦点を当てます。
観察された氷の地形とそれに伴う凍結と融解のパターン。 セクション 2 では、
モデル構成と実験計画。 セクション 3 では数値シミュレーション結果を紹介します。
海洋の成層、循環、熱輸送に焦点を当てています。 セクション 4 ではシミュレーションを比較します。
過去の研究との結果をまとめ、結論を述べています。

図 1. 所定の氷の地形 (a)、対応する伝導熱損失 (b、青線)、および底部
緯度の関数としての単位面積当たりの暖房量 (b、赤線)。 底部加熱バランスのグローバル積分
伝導熱損失。 パネル (b) の青線と赤線の間の見かけのオフセットは、海底と氷海の境界面では表面積が異なります。

図 2. 地域平均気温 (T、a)、塩分濃度の異常 (S、b)、および電位密度の異常 (ρσ、海面付近の基準圧力、c) すべてのシミュレーションの準平衡状態。 の
1 列目から 4 列目は、高い水平拡散率 (HSh) を使用した高塩分シミュレーションの結果です。
低い水平拡散率 (HSl) による高塩分シミュレーション、高い水平拡散率による低塩分シミュレーション
それぞれ、拡散率 (LSh)、および水平方向の拡散率が低い低塩分シミュレーション (LSl) です。 (a1) &
(a2)、等高線の間隔は、-2.14 ℃ より低い場合は 0.01 ℃、-2.14 ℃ より高い場合は 0.001 ℃ です。 (a3)と(a4)では輪郭が
間隔は、-0.6 ℃ より低い場合は 0.01 ℃、-0.6 ℃ より高い場合は 0.2 ℃ です。 (b1) と (b2) では、基準塩分 34.97 g /kg
が減算され、等高線間隔は 10^-3 g /kg となります。
。 (b3) と (b4) では、基準塩分 8.45 g /kg
は
を差し引くと、等高線間隔は 5×10^-4 g /kg となります。
。 (c1) と (c2) では、参照密度 1029.13 kg /m^3が差し引かれ、等高線間隔は 5 × 10^-3 kg /m^3 未満では 10^-3 kg /m^3、上部では 3 × 10^-4 kg /m^3 になります。
5×10^-3kg/m^3。 (c3) と (c4) では、参照密度 1007.7 kg /m^3
を差し引いて等高線間隔-10^-2 kg /m^3 未満では 10^-3 kg /m^3、-10^-2 kg /m^3 を超えると 5 × 10^-3 kg /m^3。

図 3. すべてのシミュレーションの準平衡状態における熱風のバランス。 (a) は 2Ω⃗・∇[u] を示し、
(b)はそれぞれ−∂[b]/r∂ϕを示します。ここで、[・]はゾーン平均を示します。 1列目から4列目まで
高水平拡散率 (HSh) を使用した高塩分シミュレーション、高塩分シミュレーションの結果です。
低い水平拡散率 (HSl)、高い水平拡散率 (LSh) を伴う低塩分シミュレーション、および
それぞれ低い水平拡散率 (LSl) を使用した塩分シミュレーション。

図 4. 帯状平均帯状速度 (u, a)、流路関数 (Ψ、時計回りの循環は次のように定義される)
正、b)、およびゾーン平均垂直運動エネルギー (w^2、対数スケールで、c) 準平衡で
すべてのシミュレーションの状態。 1 列目から 4 列目は、高塩分濃度シミュレーションの結果です。
高水平拡散率 (HSh)、高塩分濃度 低水平拡散率 (HSl)、低塩分を使用したシミュレーション
高い水平拡散率 (LSh) を使用したシミュレーション、および低い水平拡散率を使用した低塩分シミュレーション
(LS1)、それぞれ。 ストリーム関数は次のように計算されます Ψ = −∫^λx 0・∫^ r rb・vr cosφdλdr ここで、λx = 15π/180 は次のようになります。
ドメインの縦方向の範囲、v は子午線速度、λ は経度、r は半径です。 黒い
破線は接線円筒 (回転軸に平行な円筒) の境界を示します。
は底部コアに接しています)。

図 5. 帯状平均表面熱流束 (a) と帯状および垂直に統合された子午線海洋熱
すべてのシミュレーションの準平衡状態での輸送 (b、詳細については付録 B を参照)。 最初に
4 番目の列は、高い水平拡散率 (HSh)、高塩分を使用した高塩分シミュレーションの結果です。
低い水平方向の拡散率 (HSl) を使用したシミュレーション、高い水平方向の拡散率を使用した低塩分濃度のシミュレーション (LSh)、
それぞれ、水平拡散率 (LSl) が低い低塩分シミュレーションです。 (a) の黒い破線は底部加熱 (Qb)、青線は潜熱加熱 (QLH)、赤線は伝導熱損失(Qcond)です。黒い実線は表面の海洋から氷への熱流束(Qoi)です。
(b) の青い線は拡散熱流束 (FDif )、赤い線は移流熱流束 (FAdv)、黒い線は総熱量フラックス (FQ)です。
4. 議論と結論
私たちは、氷の地形と塩分が海洋の成層、循環、
そしてエンケラドゥスの熱輸送。 高塩分シナリオと低塩分シナリオの両方で、海洋上層部の温度、塩分濃度、密度はすべて緯度とともに増加します。 気温は氷点に近いです
氷と海の境界面は圧力によって変化し、氷の殻の厚さの変化によって決まります。 塩分パターンは、凍結と融解による塩分フラックスの影響を強く受けます。
高塩分海洋シミュレーションでは、密度異常は塩分異常によって支配され、
低塩分シミュレーションでは温度異常が支配的であり、定性的にはKangら。 (2022b)と一致している。
塩分濃度の低い海洋では、海底で潮汐加熱が起こり、安定した成層層が形成されます。
Zeng & Jansen (2021) が平らな上部境界を持つシミュレーションで以前に発見した海洋上部
そして熱力学的な氷と海の境界面もありません。 この地球規模の熱駆動成層は、次のような原因によって引き起こされます。
海底加熱と低塩分海洋の凝固点近くの負の熱膨張率、
したがって、表面融解によって形成される局所的に安定した塩の層状層とは異なります。
Lobo et al. 。 (2020)で議論された極地表海の「淡水レンズ」、および層別化
Kang ら(2022a、b)の「シェル加熱」シナリオ 。 ここでの層状層の深さに注意してください。
Zeng & Jansen (2021) のより理想化されたシミュレーションよりも深いですが、
Kangら(2022a,b)の「コア加熱」、低塩分の海洋 、海洋全体が層状になっています。
成層の深さ H は、垂直温度コントラスト |ΔTr|、垂直拡散率 κr、および垂直拡散熱流束の逆数 Qdif f : H ∝ κr|ΔTr|/Qdif f (Zeng &
ヤンセン 2021)。 Kang ら (2022a,b) の垂直乱流拡散率は 100 倍の大きさに設定されます。
私たちのシミュレーションと Zeng & Jansen (2021) では、層状層の深さが
Kang et al.の海の深さ。 (2022a,b)、海洋全体が層状になったままになります。 より小さい差
私たちのシミュレーションと Zeng & Jansen (2021) のシミュレーションとの間の違いは、次の点に注意することで理解できます。
Zeng & Jansen (2021) のシミュレーションでは、成層層内の熱流束は拡散性ですが、
この原稿で提示されているシミュレーションでは、垂直熱輸送の一部は移流によって行われます。
したがって、ここでの Qdif f は Zeng & Jansen (2021) よりも若干小さく、H は若干大きくなります。
私たちのシミュレーションでは、子午線熱流束の収束は変動よりもはるかに強いです。
底部加熱と表面伝導熱損失の関係。 その結果、海洋熱輸送は、
氷の凍結と融解のパターンの主な制御となり、これは以下と一致します。
Kang らの炉心加熱シナリオ (2022a) ですが、Zeng & Jansen (2021) とは異なります。
平らなアイスシェルを使用しました。 赤道から極に向かって氷の厚さが減少すると、凝固点が上昇します
緯度が高くなると、子午線方向の温度勾配が非常に強くなり、その結果、
この研究と Kang (2022a)らの子午線熱流束 と Zeng & Jansen (2021) の比較
氷の殻は平らです。
子午線熱流束は、高塩分海洋と低塩分海洋の両方でほとんどが赤道方向にあります。
アイスポンプ効果。 赤道方向の熱輸送は、次のことに注目することで定性的に理解できます。
凝固点は、氷の殻が薄くなり、海洋の熱輸送により緯度が上がるにつれて上昇します。
子午線の温度勾配に沿って下降する傾向があります。 したがって、凍結が発生するのは、
融解よりも高緯度では、極方向への氷の流れに対して氷の形状を維持できなくなります。
Kang et al. (2022a、b)にも見られるように。 より高緯度で凍結が起こるという結果
融解は、エンケラドゥスの氷の殻が平衡状態にないか、潮汐のいずれかを示しています。
氷の形状を維持するには、氷の殻内の加熱が重要です。
低塩分の海洋の成層は、海水による子午線熱輸送を強化する傾向があります。
垂直方向の温度コントラストを高めることで循環を逆転させ、
垂直方向の広がりを増大させることによる拡散と分解渦による子午線熱輸送
子午線の温度勾配。 最初のメカニズムは、Kang et al. (2022b)にも見られます。 の
彼らの炉心加熱シナリオでは、海洋の熱輸送は塩分濃度の低い海洋でより強力です。
転覆は弱いにもかかわらず、塩分濃度の高い海に。
拡散率が小さい高塩分シミュレーションでは、強化された領域で正のフィードバックが得られることがわかりました。
一方の半球での融解は、赤道を横切る逆転循環を引き起こし、それがさらに強化されます。
溶融。 このフィードバックにより、2 つの半球間の対称性が自発的に崩れる可能性があります。
ここでの具体的なシミュレーション結果では観測された氷の厚さ分布を説明することはできませんが、
同様のメカニズムが半球間の非対称性において役割を果たしている可能性があります。
エンケラドゥスの氷の殻の厚さ。 Kang らの炉心加熱シナリオでは、 (2022a)、ネガティブ
シミュレーションのような正のフィードバックの代わりに、フィードバックが提案されます。 何を説明しているのかは不明
この矛盾は、非対称の氷殻の使用に関連している可能性がありますが、
Kang らのシミュレーションにおける地形 (2022a)。 そうであれば、組み合わせた結果は次のことを示します。
正のフィードバックは、非対称性が非常に小さい限り維持されます。
エンケラドゥスでの全球海洋シミュレーションでは、解決が難しい、または計算的に不可能なプロセスが数多く存在します。 例えば、斜め対流が十分に解決できない
しかし、シミュレーションではグリッドスケールの対流の形で発生します。 さらに、氷と海の境界における潮汐と潮汐の影響は、私たちのモデルには明示的に含まれていません。考慮するのは、単に考慮するだけです。
垂直渦拡散率の選択における渦混合のためのエネルギーの提供におけるそれらの効果 (を参照)
Zeng & Jansen 2021 のセクション 2.2)。 したがって、これらのプロセスにはパラメータ化が必要です。
制約が不十分な外部パラメータ (渦拡散係数や粘度など) を導入します。
私たちの結果は、少なくとも一部の結果がこれらのパラメータ化の影響を受けやすいことを示しています。 の
全球規模の氷の衛星の海洋におけるこれらの未解決のプロセスに対する改良されたパラメータ化の開発
したがって、将来の作業ではシミュレーションが最優先されるべきです。
有益な議論とコメントをくださった Wanying Kang 氏と Edwin S. Kite に感謝します。 この作品は
シカゴ大学リサーチ コンピューティング センターから提供されたリソースを使用して完成しました。
2023年 6月 14日に提出
概要
観測データは、エンケラドゥスの氷の殻が赤道でより厚いことを示唆しています
これは、赤道から極への氷の流れを示しています。 氷の殻が平衡状態にある場合、氷の流れの物質輸送は、凍結と氷の変化によってバランスがとれなければなりません。
氷の殻の融解は、海洋の熱輸送によって調節されます。
私たちは数値海洋モデルを使用して、氷と海洋の相互作用と海洋循環を研究します。
塩分濃度が異なるエンケラドス。 塩分が根本的に決定することがわかりました
海洋の成層。 塩分濃度の低い海では層状の層が形成され、海洋に影響を与えます。
海洋循環と熱輸送。 しかし、氷の潮汐加熱がなければ、
シェルの場合、海洋の熱輸送は常に赤道方向であることが判明し、その結果凍結が起こります。
極点では氷が溶け、低緯度では氷の殻の形状を維持できなくなります。
赤道から極地までの氷の流れに逆らって。 シミュレーション結果は、氷が
エンケラドゥスの殻が平衡状態にない、または氷殻内の潮汐散逸が
氷の殻の形状を維持する上で重要です。
キーワード: エンケラドゥス – 塩分 – 成層層 – 海洋熱輸送 – 氷の形状
1. はじめに
エンケラドゥスには、全球規模の氷の殻の下に深さ約40kmの海があると考えられています。
(例、Postberg et al. 2011; Patthoff & Kattenhorn 2011; Thomas et al. 2016)。 エネルギー源
衛星全体の液体の海洋と南極地域での約10GWの熱損失を維持している
(Spencer et al. 2006; Howett et al. 2011; Spencer et al. 2013) は主に潮汐に由来すると考えられています。
散逸。 一般に、潮汐の消散は、氷の殻、海洋、および海域で起こると予想されます。
しっかりとしたコア。 海洋の潮汐加熱は、海洋の潮汐加熱に比べて無視できると考えられてきました。
氷の殻と内部の固体コア (例、Chen & Nimmo 2011; Tyler 2011; Chen et al. 2014; Beuthe
2016年; ヘイ&マツヤマ 2017; 松山ほか 2018年; ヘイ&マツヤマ 2019)。 最近ではありますが
研究は、共鳴が発生した場合、内部潮汐の消散が層状海洋でより多くの熱を生成する可能性があることを示唆しています
発生する(Rovira-Navarro et al. 2023)、エンケラドゥスの海洋の層状化(例、Kang et al. 2022b)
熱損失に匹敵する熱生成率をサポートできるほど強力である可能性は低い
レート。 氷殻内での潮汐散逸と、導管内での水の乱流散逸
南極 (Kite & Rubin 2016) は O(10 GW) に達する可能性があると主張されています (Beuthe 2019;Souˇcek et al. 2019)。
しかし、エンケラドゥスの氷のレオロジーはほとんど理解されていない。
氷殻内の潮汐散逸速度に影響を与えます。 エンケラドゥスの密度が低いことは、コアが
は多孔質であり、これがおそらくコア内での強力な潮汐散逸をサポートしており、O(10 GW)に達します(Iess et al.
2014年; ロバーツ 2015; カデックら。 〜 2016年; ショブレットら。 2017)。 解放は次の原因となるとも主張されている
海洋における散逸加熱は最大 O(0.1 GW) (Lemasquerier et al. 2017; Wilson & Kerswell)
2018年; レキエルら。 2019年; ソーダーランドら。 2020年)。 潮汐加熱の一部は
固体コアと氷の殻は依然として非常に不確実であり、底部の固体コアからのいくらかの加熱は、
それがエンケラドゥスの海洋循環を根本的に形作ると予想されています。
エンケラドゥスの氷の殻の厚さは平均約 20 km で、平らではありません。最も厚いのは、
赤道(30km以上)で最も薄いのは南極地域(10km未満)です。 もあります。
氷の殻の半球間非対称性。氷は北極よりも南極の方が薄い。
ポール (Beuthe et al. 2016; Cadek et al. ˇ 2019; Hemingway & Mittal 2019)。 顕著な勾配
氷の殻の厚さは、赤道から極への氷の流れを示唆しています。 エンケラドゥスの氷殻が
平衡状態では、氷の流れの赤道から極への物質移動は、氷の凍結によってバランスが保たれなければなりません
赤道で、極で溶けます。 氷殻モデルは一般に、凍結/融解を予測します。
エンケラドゥスでは、赤道から極地までの氷の流れのバランスをとるために、年間数ミリメートルの速度2が必要です。
または同等の、O(0.01 W /m^2) 潜熱 (Cadek et al. ˇ 2019; Kang & Flierl 2020; Kang et al. ˇ 2019; Kang et al.2022b)。
氷の凍結と融解は、熱収支、つまり関連する潜熱 (QLH、融解を正として定義) は、熱伝導性熱損失間の不均衡と一致する必要があります。
氷殻の底部 (Qcond) と海洋から氷への熱流束 (Qoi): Qcond + QLH = Qoi。
氷と海の境界面での伝導熱流束は、次のように氷の殻の厚さによって調整されます。
氷殻(Qi)内の潮汐加熱も同様です。 氷殻内で強く局所的な潮汐加熱がなければ、
氷が最も薄い極地では伝導熱損失が最も大きく、氷の凍結が促進されます。
極では、氷の形状を維持するために必要なことの逆です。 潮の干満
氷の殻は極地で最も強く、増幅されるため、この問題に対する可能な答えである可能性があります。
氷が薄い場合 (例: Beuthe 2018、2019; Kang & Flierl 2020)、したがって潜在的に
極での溶解用。 あるいは、海洋からの熱流束 Qoi は、
ポール。 氷への全球の海洋熱流束は、底部固体コアの潮汐加熱から来ます。
ピークは極点にありますが (Choblet et al. 2017)、その空間パターンは海洋循環によって調整されます。
これがこの文書の焦点です。
これまでの研究では、エンケラドゥスや他の氷の衛星における全球規模の海洋循環が調査されてきました。
(Soderlund et al. 2014; Travis & Schubert 2015; Soderlund 2019; Amit et al. 2020; Lobo et al. 2020;
カンら。 2020年; ゼン&ヤンセン 2021; アシュケナージ&ツィペルマン 2021; ビレら。 2022年; クヴォルカ&
カデック 〜 2022; カン 2022; カン&ジャンセン 2022; カンら。 2022a、b; ジャンセンら。 2023年)。 これらの研究
さまざまな方法(概念モデル、海洋のみの数値シミュレーション、
氷と海洋を組み合わせた数値シミュレーションなど)を、2 次元または 3 次元の領域で、幅広い範囲で実行できます。
パラメータとさまざまな境界条件。 ただし、3 次元のグローバル ドメインで完全に結合した氷海洋熱力学を使用したシミュレーションはまだ行われていません。 公開されているシミュレーション結果
おそらく大規模な影響の結果として、海洋循環と海洋氷の熱流束が大きく異なります。
外部パラメータの不確実性と、地球規模の海洋を現実的にモデル化することの難しさ
パラメータ体制。 したがって、エンケラドゥスの海洋循環と熱輸送の実際の体制
は不確実なままです。
海洋循環と熱輸送を決定する重要な要素の 1 つは塩分 (S) です。 塩分濃度
水の状態方程式を決定し、海洋の成層と循環に影響を与えます。 多くの
重要なのは、塩分濃度が臨界値よりも低い場合、熱膨張率 (α ≡ −(1/ρ)(∂ρ/∂T)
ここで、ρ は密度、T は温度です) は凝固点付近では負になります。 結果として、このような低水準では、
塩分の多い海洋では、海底加熱により安定した成層層が海洋上部に形成されます(Melosh et al.2004年; ゼン&ヤンセン 2021)。 負の熱膨張率が存在するためのしきい値。
負の熱膨張率が存在するためのしきい値。
エンケラドゥスの海の圧力は約20 g /kg(Zeng & Jansen 2021; Kang et al. 2022b)。
観察に基づいて、エンケラドゥスの海の塩分を推定するにはさまざまな方法があります。
塩分が豊富な氷粒の存在(Postberg et al. 2009)、シリカナノ粒子の存在(Hsu et al. 2015)、
氷導管内の沸騰水のモデルを使用 (Ingersoll & 中島 2016)、平衡水岩
相互作用 (Zolotov 2007)、海洋地球化学 (Glein et al. 2018)、および海洋熱輸送 (Kang他。 2022b)。
推定値は研究ごとに異なり、2 ~ 40 g /kg の広い範囲が与えられます。
。 したがって、両方とも「高塩分」(S > 20 g /kg)および「低塩分」(S < 20 g /kg) シナリオは慎重に行う必要があります
エンケラドゥスの海洋循環を研究するときに考慮されました。
塩分濃度は、表面密度のコントラストによって引き起こされる逆転循環にも影響を与える可能性があります。
海洋の熱輸送を調整し、氷の形状にさらに影響を与えます。 カンら。 (2022b)
規定の氷の厚さで海洋循環をモデル化し、極での融解速度を規定し、
氷の厚さによって引き起こされる推定氷の流れのバランスをとるために必要な、赤道での凍結速度
勾配。 彼らは、赤道と極の間の表面密度のコントラストが影響を及ぼしていることを発見しました。
各半球の循環を覆す。 循環の方向は平均値に依存します
海洋の塩分濃度は高いが、海洋の熱輸送は常に赤道方向であることがわかっている。
極点(氷が薄いため圧力が低い)の凝固点は赤道よりも高い
(氷が厚いため圧力が高くなります)、熱輸送は常に暖かい極から行われます。
寒い赤道へ。 赤道方向の海洋熱輸送は、極点での凍結と融解を促進します。
赤道にあるため、赤道から極までの氷殻の厚さの勾配を減少させるように作用します。
アイスポンプ効果として知られています (Lewis & Perkin 1986)。
氷の殻と底部の固体コアの間の潮汐加熱の分配も影響を与える可能性があります。
海洋の熱輸送は、2 つの半球間の非対称な氷殻の形状にさらに影響を与えます。
カンら。 (2022a) 氷がわずかに存在する半球間の非対称性を持つ氷の幾何学形状を規定する
南半球ではさらに薄い。 完全に結合した氷海の熱力学を組み込んでいます。
氷の殻と底部の固体コアの両方で潮汐散逸を伴う 2 次元ドメイン。 彼らがそれを発見したのは、
加熱は氷殻内の潮汐散逸によって支配され、南ではより強い融解が起こる
北よりも極に位置し、逆転した循環により熱が南に運ばれ、熱が増加します。
非対称性。 代わりに、加熱が主に中心部で行われる場合、中心部での凍結がより強くなります。
南極は北極よりも高く、転倒によって熱が北に運ばれるため、
非対称。
今回我々は、海洋熱輸送に焦点を当て、エンケラドゥスにおける海洋循環と氷海洋相互作用に対する塩分濃度の影響を研究する。 私たちは、
マサチューセッツ工科大学の全身循環モデル (MITgcm) (Adcroft et al. 2018)、
所定の氷の形状と完全に結合した氷と海の熱力学を備えています。 潮汐加熱を除く
固体コアからの海洋熱輸送が氷の中で維持できるかどうかに特に焦点を当てます。
観察された氷の地形とそれに伴う凍結と融解のパターン。 セクション 2 では、
モデル構成と実験計画。 セクション 3 では数値シミュレーション結果を紹介します。
海洋の成層、循環、熱輸送に焦点を当てています。 セクション 4 ではシミュレーションを比較します。
過去の研究との結果をまとめ、結論を述べています。

図 1. 所定の氷の地形 (a)、対応する伝導熱損失 (b、青線)、および底部
緯度の関数としての単位面積当たりの暖房量 (b、赤線)。 底部加熱バランスのグローバル積分
伝導熱損失。 パネル (b) の青線と赤線の間の見かけのオフセットは、海底と氷海の境界面では表面積が異なります。

図 2. 地域平均気温 (T、a)、塩分濃度の異常 (S、b)、および電位密度の異常 (ρσ、海面付近の基準圧力、c) すべてのシミュレーションの準平衡状態。 の
1 列目から 4 列目は、高い水平拡散率 (HSh) を使用した高塩分シミュレーションの結果です。
低い水平拡散率 (HSl) による高塩分シミュレーション、高い水平拡散率による低塩分シミュレーション
それぞれ、拡散率 (LSh)、および水平方向の拡散率が低い低塩分シミュレーション (LSl) です。 (a1) &
(a2)、等高線の間隔は、-2.14 ℃ より低い場合は 0.01 ℃、-2.14 ℃ より高い場合は 0.001 ℃ です。 (a3)と(a4)では輪郭が
間隔は、-0.6 ℃ より低い場合は 0.01 ℃、-0.6 ℃ より高い場合は 0.2 ℃ です。 (b1) と (b2) では、基準塩分 34.97 g /kg
が減算され、等高線間隔は 10^-3 g /kg となります。
。 (b3) と (b4) では、基準塩分 8.45 g /kg
は
を差し引くと、等高線間隔は 5×10^-4 g /kg となります。
。 (c1) と (c2) では、参照密度 1029.13 kg /m^3が差し引かれ、等高線間隔は 5 × 10^-3 kg /m^3 未満では 10^-3 kg /m^3、上部では 3 × 10^-4 kg /m^3 になります。
5×10^-3kg/m^3。 (c3) と (c4) では、参照密度 1007.7 kg /m^3
を差し引いて等高線間隔-10^-2 kg /m^3 未満では 10^-3 kg /m^3、-10^-2 kg /m^3 を超えると 5 × 10^-3 kg /m^3。

図 3. すべてのシミュレーションの準平衡状態における熱風のバランス。 (a) は 2Ω⃗・∇[u] を示し、
(b)はそれぞれ−∂[b]/r∂ϕを示します。ここで、[・]はゾーン平均を示します。 1列目から4列目まで
高水平拡散率 (HSh) を使用した高塩分シミュレーション、高塩分シミュレーションの結果です。
低い水平拡散率 (HSl)、高い水平拡散率 (LSh) を伴う低塩分シミュレーション、および
それぞれ低い水平拡散率 (LSl) を使用した塩分シミュレーション。

図 4. 帯状平均帯状速度 (u, a)、流路関数 (Ψ、時計回りの循環は次のように定義される)
正、b)、およびゾーン平均垂直運動エネルギー (w^2、対数スケールで、c) 準平衡で
すべてのシミュレーションの状態。 1 列目から 4 列目は、高塩分濃度シミュレーションの結果です。
高水平拡散率 (HSh)、高塩分濃度 低水平拡散率 (HSl)、低塩分を使用したシミュレーション
高い水平拡散率 (LSh) を使用したシミュレーション、および低い水平拡散率を使用した低塩分シミュレーション
(LS1)、それぞれ。 ストリーム関数は次のように計算されます Ψ = −∫^λx 0・∫^ r rb・vr cosφdλdr ここで、λx = 15π/180 は次のようになります。
ドメインの縦方向の範囲、v は子午線速度、λ は経度、r は半径です。 黒い
破線は接線円筒 (回転軸に平行な円筒) の境界を示します。
は底部コアに接しています)。

図 5. 帯状平均表面熱流束 (a) と帯状および垂直に統合された子午線海洋熱
すべてのシミュレーションの準平衡状態での輸送 (b、詳細については付録 B を参照)。 最初に
4 番目の列は、高い水平拡散率 (HSh)、高塩分を使用した高塩分シミュレーションの結果です。
低い水平方向の拡散率 (HSl) を使用したシミュレーション、高い水平方向の拡散率を使用した低塩分濃度のシミュレーション (LSh)、
それぞれ、水平拡散率 (LSl) が低い低塩分シミュレーションです。 (a) の黒い破線は底部加熱 (Qb)、青線は潜熱加熱 (QLH)、赤線は伝導熱損失(Qcond)です。黒い実線は表面の海洋から氷への熱流束(Qoi)です。
(b) の青い線は拡散熱流束 (FDif )、赤い線は移流熱流束 (FAdv)、黒い線は総熱量フラックス (FQ)です。
4. 議論と結論
私たちは、氷の地形と塩分が海洋の成層、循環、
そしてエンケラドゥスの熱輸送。 高塩分シナリオと低塩分シナリオの両方で、海洋上層部の温度、塩分濃度、密度はすべて緯度とともに増加します。 気温は氷点に近いです
氷と海の境界面は圧力によって変化し、氷の殻の厚さの変化によって決まります。 塩分パターンは、凍結と融解による塩分フラックスの影響を強く受けます。
高塩分海洋シミュレーションでは、密度異常は塩分異常によって支配され、
低塩分シミュレーションでは温度異常が支配的であり、定性的にはKangら。 (2022b)と一致している。
塩分濃度の低い海洋では、海底で潮汐加熱が起こり、安定した成層層が形成されます。
Zeng & Jansen (2021) が平らな上部境界を持つシミュレーションで以前に発見した海洋上部
そして熱力学的な氷と海の境界面もありません。 この地球規模の熱駆動成層は、次のような原因によって引き起こされます。
海底加熱と低塩分海洋の凝固点近くの負の熱膨張率、
したがって、表面融解によって形成される局所的に安定した塩の層状層とは異なります。
Lobo et al. 。 (2020)で議論された極地表海の「淡水レンズ」、および層別化
Kang ら(2022a、b)の「シェル加熱」シナリオ 。 ここでの層状層の深さに注意してください。
Zeng & Jansen (2021) のより理想化されたシミュレーションよりも深いですが、
Kangら(2022a,b)の「コア加熱」、低塩分の海洋 、海洋全体が層状になっています。
成層の深さ H は、垂直温度コントラスト |ΔTr|、垂直拡散率 κr、および垂直拡散熱流束の逆数 Qdif f : H ∝ κr|ΔTr|/Qdif f (Zeng &
ヤンセン 2021)。 Kang ら (2022a,b) の垂直乱流拡散率は 100 倍の大きさに設定されます。
私たちのシミュレーションと Zeng & Jansen (2021) では、層状層の深さが
Kang et al.の海の深さ。 (2022a,b)、海洋全体が層状になったままになります。 より小さい差
私たちのシミュレーションと Zeng & Jansen (2021) のシミュレーションとの間の違いは、次の点に注意することで理解できます。
Zeng & Jansen (2021) のシミュレーションでは、成層層内の熱流束は拡散性ですが、
この原稿で提示されているシミュレーションでは、垂直熱輸送の一部は移流によって行われます。
したがって、ここでの Qdif f は Zeng & Jansen (2021) よりも若干小さく、H は若干大きくなります。
私たちのシミュレーションでは、子午線熱流束の収束は変動よりもはるかに強いです。
底部加熱と表面伝導熱損失の関係。 その結果、海洋熱輸送は、
氷の凍結と融解のパターンの主な制御となり、これは以下と一致します。
Kang らの炉心加熱シナリオ (2022a) ですが、Zeng & Jansen (2021) とは異なります。
平らなアイスシェルを使用しました。 赤道から極に向かって氷の厚さが減少すると、凝固点が上昇します
緯度が高くなると、子午線方向の温度勾配が非常に強くなり、その結果、
この研究と Kang (2022a)らの子午線熱流束 と Zeng & Jansen (2021) の比較
氷の殻は平らです。
子午線熱流束は、高塩分海洋と低塩分海洋の両方でほとんどが赤道方向にあります。
アイスポンプ効果。 赤道方向の熱輸送は、次のことに注目することで定性的に理解できます。
凝固点は、氷の殻が薄くなり、海洋の熱輸送により緯度が上がるにつれて上昇します。
子午線の温度勾配に沿って下降する傾向があります。 したがって、凍結が発生するのは、
融解よりも高緯度では、極方向への氷の流れに対して氷の形状を維持できなくなります。
Kang et al. (2022a、b)にも見られるように。 より高緯度で凍結が起こるという結果
融解は、エンケラドゥスの氷の殻が平衡状態にないか、潮汐のいずれかを示しています。
氷の形状を維持するには、氷の殻内の加熱が重要です。
低塩分の海洋の成層は、海水による子午線熱輸送を強化する傾向があります。
垂直方向の温度コントラストを高めることで循環を逆転させ、
垂直方向の広がりを増大させることによる拡散と分解渦による子午線熱輸送
子午線の温度勾配。 最初のメカニズムは、Kang et al. (2022b)にも見られます。 の
彼らの炉心加熱シナリオでは、海洋の熱輸送は塩分濃度の低い海洋でより強力です。
転覆は弱いにもかかわらず、塩分濃度の高い海に。
拡散率が小さい高塩分シミュレーションでは、強化された領域で正のフィードバックが得られることがわかりました。
一方の半球での融解は、赤道を横切る逆転循環を引き起こし、それがさらに強化されます。
溶融。 このフィードバックにより、2 つの半球間の対称性が自発的に崩れる可能性があります。
ここでの具体的なシミュレーション結果では観測された氷の厚さ分布を説明することはできませんが、
同様のメカニズムが半球間の非対称性において役割を果たしている可能性があります。
エンケラドゥスの氷の殻の厚さ。 Kang らの炉心加熱シナリオでは、 (2022a)、ネガティブ
シミュレーションのような正のフィードバックの代わりに、フィードバックが提案されます。 何を説明しているのかは不明
この矛盾は、非対称の氷殻の使用に関連している可能性がありますが、
Kang らのシミュレーションにおける地形 (2022a)。 そうであれば、組み合わせた結果は次のことを示します。
正のフィードバックは、非対称性が非常に小さい限り維持されます。
エンケラドゥスでの全球海洋シミュレーションでは、解決が難しい、または計算的に不可能なプロセスが数多く存在します。 例えば、斜め対流が十分に解決できない
しかし、シミュレーションではグリッドスケールの対流の形で発生します。 さらに、氷と海の境界における潮汐と潮汐の影響は、私たちのモデルには明示的に含まれていません。考慮するのは、単に考慮するだけです。
垂直渦拡散率の選択における渦混合のためのエネルギーの提供におけるそれらの効果 (を参照)
Zeng & Jansen 2021 のセクション 2.2)。 したがって、これらのプロセスにはパラメータ化が必要です。
制約が不十分な外部パラメータ (渦拡散係数や粘度など) を導入します。
私たちの結果は、少なくとも一部の結果がこれらのパラメータ化の影響を受けやすいことを示しています。 の
全球規模の氷の衛星の海洋におけるこれらの未解決のプロセスに対する改良されたパラメータ化の開発
したがって、将来の作業ではシミュレーションが最優先されるべきです。
有益な議論とコメントをくださった Wanying Kang 氏と Edwin S. Kite に感謝します。 この作品は
シカゴ大学リサーチ コンピューティング センターから提供されたリソースを使用して完成しました。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます