
長期地上測光と宇宙測光から発見された準惑星(136199)エリスの潮汐ロックされた自転
2022年11月15日
概要
準惑星のメンバーの回転状態 - 海王星以遠領域の衛星システムは、形成によって決定されます
条件とコンポーネント間の潮汐相互作用、およびこれらの回転特性は、それらの進化の主要なトレーサーです。
これまで、多くの著者が準惑星エリスの自転周期について非常に多様な値を主張していた。
その衛星であるディスノミアの公転周期 (15.8 d) と (ほぼ) 同期した自転までの時間です。この手紙で私たちは新しい光を提示します
~1-2mクラスの地上望遠鏡、およびTESSとガイア宇宙望遠鏡で撮影されたエリスの曲線データ。 TESS データは
明確に定義された光度曲線期間を提供しませんが、光度曲線の変動を可能な最大光度曲線振幅に制限する可能性があります
P ≤ 24 時間の期間で ∆m ≤ 0.03 mag (1-σ) の。結合された地上データとガイア測定値の両方が明確に指摘しています
ディスノミアの軌道周期に等しい光度曲線の周期、P = 15.8 d、Δm ≈ 0.03 mag の光度曲線の振幅、つまり
エリスの回転は潮汐ロック。ディスノミアに衝突起源があると仮定し、単純な潮汐進化モデルで計算
エリスの速度を落とすには、ディスノミアが比較的大きく (q = 0.01–0.03 の質量比)、大きくなければならない (Rs ≥ 300 km) 必要があることを示しています。
同期回転。これらのシミュレーションは、次のことも示しています。
– ディスノミアの密度は 1.8 ~ 2.4 g /cm^3 にする必要があります
、同様のサイズの海王星以遠天体の中で非常に高い値であり、形成条件に関する重要な制約。
キーワード。方法: 観測、技法: 測光、カイパー ベルト天体: エリス-ディスノミア

図 1. C(P,∆m) 等高線図。 最も顕著な極小値は、ディスノミアの軌道周期に非常に近い約 16 日の周期で識別されます。
15.78 d (詳細は本文を参照)。
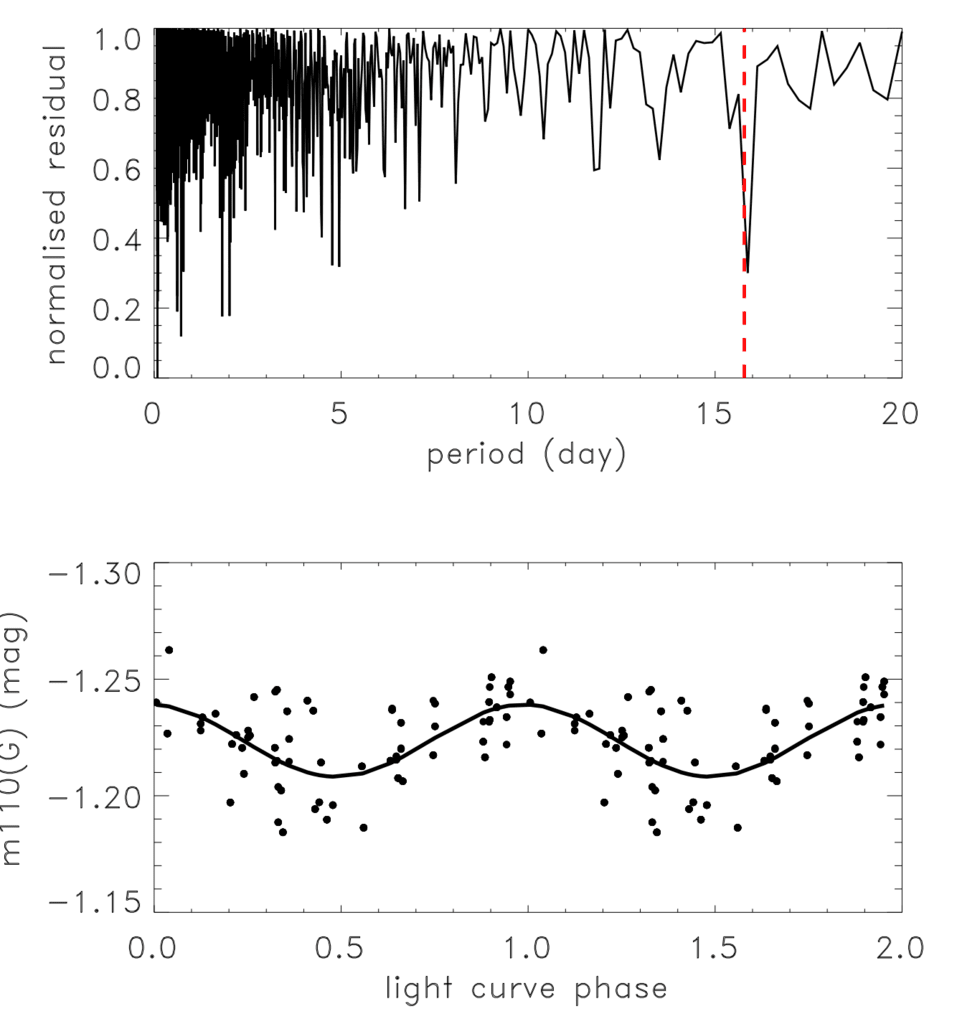
図2 上段:エリスガイアの正規化残差スペクトル
光曲線。 赤い破線は P = 15.78 d、軌道周期
失神; 下のパネル: f = 0.063 c/d で折り畳まれたガイア光曲線。
実線の曲線は、ピーク間振幅が の最適な正弦曲線です。
Δm = 0.031±0.001。
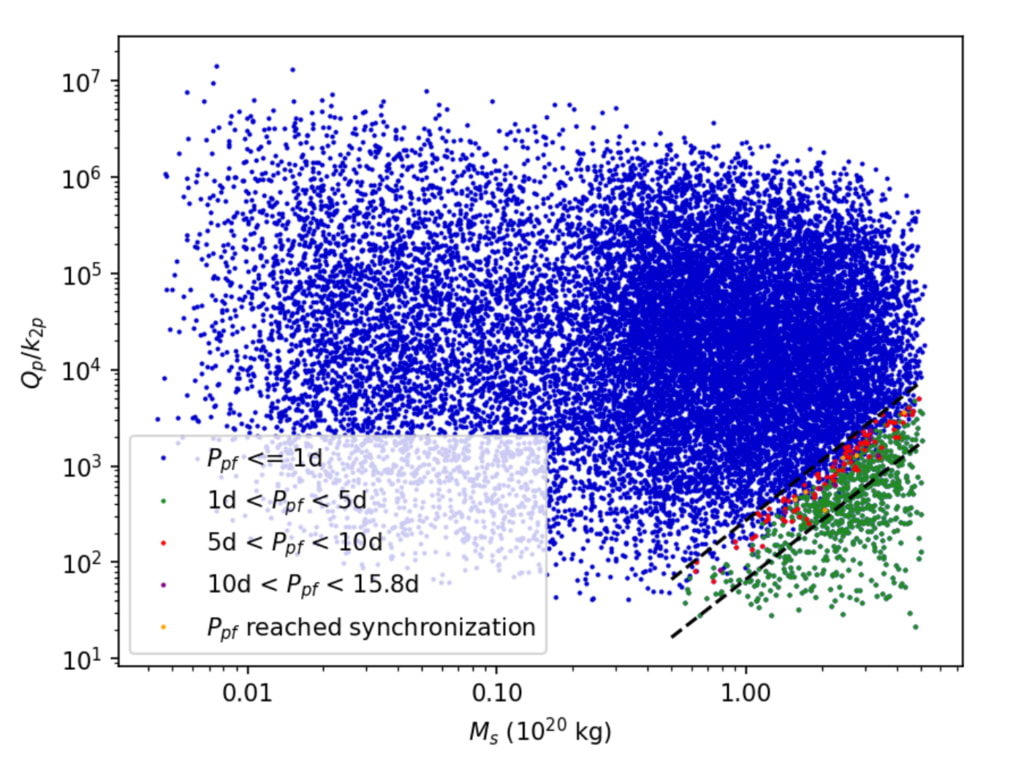
図 3. Qp/k2p ディスノミアの質量 Ms
最初の試運転で。
オレンジ色のシンボルは、最終的に同期エリスになったケースを示しています
回転; 青い記号は、P < 1 d の最終エリス回転のケースを表します
ピリオド。 破線は、リードする M–Qp/k2p 値の領域を示します。
エリスの回転または潮汐同期を遅くするため(テキストを参照)
詳細。)
4. 結論
この論文では、長期的な地上ベースの測光を分析しました
との測定によって補完されたエリスの観測
TESSとガイア宇宙望遠鏡。 TESSデータはそうではありませんでしたが、
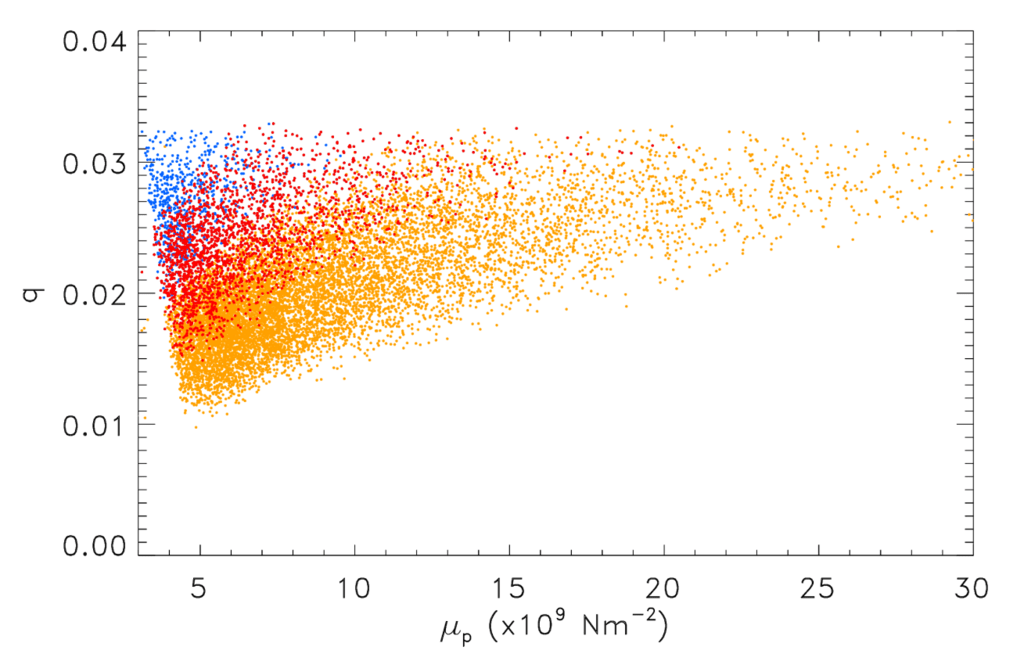
図 4. ディスノミアとエリスの質量比 (q) とエリスの剛性 (µp)
エリスが同期回転になったときのそれらのシミュレーション実行で。
オレンジ、赤、青の色は、Qp = 50 のエリス潮汐パラメーターを示します。
100 と 200 (±10%)。
決定的な回転期間を提供し、結合された地上ベースの測定値とガイア データの両方が明確に示しています。
ディスノミアの軌道周期に等しい光度曲線の周期、すなわちエリスの潮汐固定回転。エリスの同期回転 – これは、
エリスの衛星ディスノミアとの潮汐相互作用 – 制約を課す
衛星の重要な物理的特性、および
セクションで議論されるように、エリスのもの。 A.6.ライトカーブ
または潮汐進化の結果が形状を直接制約しない、
スピン率が非常に低いため、エリスの形状は次のようになると予想されます。
冥王星と冥王星で観察されたものと同様に、球形に非常に近い
Charon (Nimmo et al. 2017)。 Eris の場合、Maclaurin 形状の均一密度内部モデル、または Darwin-Radau の両方
モデル (Murray & Dermott 2000 などを参照)、
岩のコアと氷のマントルの内部は平坦化の価値を提供します
≤ 0.0001。これはまた、掩蔽の形と大きさを意味します。
解 (Sicardy et al. 2011) は、R = 1163±6 km の球面解に非常に近くなければなりません。為に
熱放射モデル。また、(Holler et al. 2021) が提案した
の非ケプラー軌道の考えられる原因としての扁球エリス
今では可能性が低いオプションのように思われるディスノミア。
非ケプラー ディスノミア軌道の別の説明
光の中心 - 体の中心 (CoL-CoB) オフセット
表面またはエリスの大きなアルベド パターンによるものです。私たちが調査した Δm = 0.031 mag の振幅が最も適切であることを考慮してください。
このシナリオは、赤道上の単一のスポット、ディスノミアの軌道面との一致、および (Holler et al.
2021年)。私たちの単純なモデルでは、スポットはわずかに見えます
回転段階であり、他の段階では完全に見えません。これらの中で
後者の場合、エリスは均質で高アルベド面を持っています。私達
スポットアルベドを使用してスポットのサイズを変化させた
必要な光度曲線の振幅を常に生成し、
Lommel-Seeliger と Lambert の散乱法則の両方を考慮しました。
この光度曲線の振幅で最大 CoL-CoB オフセット
取得できる距離は、ロンメル-ゼーリガーの両方で約 40 km です。
ランバート散乱とほぼ同様の値が、考慮されるアルベドの全範囲で得られます。これは多くの
Holler らによって得られた 462 km のオフセットよりも小さい。 (2021)。
Dysno mia の最大可能サイズが約 600 km であることを考慮すると、CoL-CoB の支配的な部分が
オフセットは、衛星の表面の特徴に起因する可能性があります。
CoL-CoB オフセットは、非ケプラー軌道の理由とは考えにくいです。ディスノミアの非ケプラー軌道も引き起こされる可能性があります
衛星の非球形によって。海王星横断天体のケプラー/K2 光曲線に関する最近の研究 (Kecskeméthy
ら。 2022) は、TNO の光度曲線の振幅が残っていることを示しています。
メインの非球面性が大きい(D & 400 km)サイズで大きい
ベルトの小惑星は大幅に減少します (Vernazza et al. 2021)。その間
これは、より大きな領域での不規則から球状への遷移が原因である可能性があります
TNO のサイズ、それらの一般的な低密度と高気孔率
このシナリオに反対します。ディスノミアの予想サイズ
(D & 600 km) オブジェクトは、より高くても、かなり丸いはずです。
密度とかなりの内部強度。
巨人の中でエリス・ディスノミア系が形成されたと仮定すると
衝突後のエリスの回転期間は、おそらくはるかに短く、数時間程度でした。この高速回転は、ディスノミアとの潮汐相互作用によって減速されなければなりませんでした。上に示したように、同期回転に到達するには
期間ディスノミアは比較的大規模である必要があります(質量比の
q = 0.02-0.03)、Eris の Qp 潮汐消散係数と µp 剛性の正準値を仮定。この質量比は 2 番目の
〜8:1の比率の後の海王星以遠領域での最大値
冥王星・カロン系 (Barr & Schwamb 2016; Arakawa を参照)
ら。 2019;キス等。 2019、以前の評価の場合)。 (私たちは注意します
現在、Orcus-Vanth システムの質量比はむしろ
不明)。比較的高い質量比は、高いディスノミア密度 ρs = 1.8-2.4 g/ cm^3。
この中の海王星以遠天体の典型的な密度よりも大きい
サイズ範囲、ρ = 0.5-1.0 g/ cm^3
(例えば Bierson & Nimmo 2019 を参照)。
私たちの潮汐進化モデルでは、従来にない低い Qp 潮汐消散係数により、ディスノミア密度を低くすることができます(から ρs ≈ 1.2g cm−3) とエリスは で同期回転に達します
しかし同時に、これらの値は依然として R ≈ 300 km 天体の典型的な低密度を上回っており、
低レベルの気孔率。衝突シミュレーションは、
一般に、10−3 ≤ q ≤ 10−1 の無傷の衛星
で形成することができます
広範囲の影響パラメータを想定した海王星以遠領域 (Arakawa et al. 2019)。より詳細な影響と潮汐進化のシミュレーションにより、発生する条件を特定できるはずです。
現在の高密度エリス - 高密度ディスノミア系につながる可能性があります。
2022年11月15日
概要
準惑星のメンバーの回転状態 - 海王星以遠領域の衛星システムは、形成によって決定されます
条件とコンポーネント間の潮汐相互作用、およびこれらの回転特性は、それらの進化の主要なトレーサーです。
これまで、多くの著者が準惑星エリスの自転周期について非常に多様な値を主張していた。
その衛星であるディスノミアの公転周期 (15.8 d) と (ほぼ) 同期した自転までの時間です。この手紙で私たちは新しい光を提示します
~1-2mクラスの地上望遠鏡、およびTESSとガイア宇宙望遠鏡で撮影されたエリスの曲線データ。 TESS データは
明確に定義された光度曲線期間を提供しませんが、光度曲線の変動を可能な最大光度曲線振幅に制限する可能性があります
P ≤ 24 時間の期間で ∆m ≤ 0.03 mag (1-σ) の。結合された地上データとガイア測定値の両方が明確に指摘しています
ディスノミアの軌道周期に等しい光度曲線の周期、P = 15.8 d、Δm ≈ 0.03 mag の光度曲線の振幅、つまり
エリスの回転は潮汐ロック。ディスノミアに衝突起源があると仮定し、単純な潮汐進化モデルで計算
エリスの速度を落とすには、ディスノミアが比較的大きく (q = 0.01–0.03 の質量比)、大きくなければならない (Rs ≥ 300 km) 必要があることを示しています。
同期回転。これらのシミュレーションは、次のことも示しています。
– ディスノミアの密度は 1.8 ~ 2.4 g /cm^3 にする必要があります
、同様のサイズの海王星以遠天体の中で非常に高い値であり、形成条件に関する重要な制約。
キーワード。方法: 観測、技法: 測光、カイパー ベルト天体: エリス-ディスノミア

図 1. C(P,∆m) 等高線図。 最も顕著な極小値は、ディスノミアの軌道周期に非常に近い約 16 日の周期で識別されます。
15.78 d (詳細は本文を参照)。

図2 上段:エリスガイアの正規化残差スペクトル
光曲線。 赤い破線は P = 15.78 d、軌道周期
失神; 下のパネル: f = 0.063 c/d で折り畳まれたガイア光曲線。
実線の曲線は、ピーク間振幅が の最適な正弦曲線です。
Δm = 0.031±0.001。

図 3. Qp/k2p ディスノミアの質量 Ms
最初の試運転で。
オレンジ色のシンボルは、最終的に同期エリスになったケースを示しています
回転; 青い記号は、P < 1 d の最終エリス回転のケースを表します
ピリオド。 破線は、リードする M–Qp/k2p 値の領域を示します。
エリスの回転または潮汐同期を遅くするため(テキストを参照)
詳細。)
4. 結論
この論文では、長期的な地上ベースの測光を分析しました
との測定によって補完されたエリスの観測
TESSとガイア宇宙望遠鏡。 TESSデータはそうではありませんでしたが、

図 4. ディスノミアとエリスの質量比 (q) とエリスの剛性 (µp)
エリスが同期回転になったときのそれらのシミュレーション実行で。
オレンジ、赤、青の色は、Qp = 50 のエリス潮汐パラメーターを示します。
100 と 200 (±10%)。
決定的な回転期間を提供し、結合された地上ベースの測定値とガイア データの両方が明確に示しています。
ディスノミアの軌道周期に等しい光度曲線の周期、すなわちエリスの潮汐固定回転。エリスの同期回転 – これは、
エリスの衛星ディスノミアとの潮汐相互作用 – 制約を課す
衛星の重要な物理的特性、および
セクションで議論されるように、エリスのもの。 A.6.ライトカーブ
または潮汐進化の結果が形状を直接制約しない、
スピン率が非常に低いため、エリスの形状は次のようになると予想されます。
冥王星と冥王星で観察されたものと同様に、球形に非常に近い
Charon (Nimmo et al. 2017)。 Eris の場合、Maclaurin 形状の均一密度内部モデル、または Darwin-Radau の両方
モデル (Murray & Dermott 2000 などを参照)、
岩のコアと氷のマントルの内部は平坦化の価値を提供します
≤ 0.0001。これはまた、掩蔽の形と大きさを意味します。
解 (Sicardy et al. 2011) は、R = 1163±6 km の球面解に非常に近くなければなりません。為に
熱放射モデル。また、(Holler et al. 2021) が提案した
の非ケプラー軌道の考えられる原因としての扁球エリス
今では可能性が低いオプションのように思われるディスノミア。
非ケプラー ディスノミア軌道の別の説明
光の中心 - 体の中心 (CoL-CoB) オフセット
表面またはエリスの大きなアルベド パターンによるものです。私たちが調査した Δm = 0.031 mag の振幅が最も適切であることを考慮してください。
このシナリオは、赤道上の単一のスポット、ディスノミアの軌道面との一致、および (Holler et al.
2021年)。私たちの単純なモデルでは、スポットはわずかに見えます
回転段階であり、他の段階では完全に見えません。これらの中で
後者の場合、エリスは均質で高アルベド面を持っています。私達
スポットアルベドを使用してスポットのサイズを変化させた
必要な光度曲線の振幅を常に生成し、
Lommel-Seeliger と Lambert の散乱法則の両方を考慮しました。
この光度曲線の振幅で最大 CoL-CoB オフセット
取得できる距離は、ロンメル-ゼーリガーの両方で約 40 km です。
ランバート散乱とほぼ同様の値が、考慮されるアルベドの全範囲で得られます。これは多くの
Holler らによって得られた 462 km のオフセットよりも小さい。 (2021)。
Dysno mia の最大可能サイズが約 600 km であることを考慮すると、CoL-CoB の支配的な部分が
オフセットは、衛星の表面の特徴に起因する可能性があります。
CoL-CoB オフセットは、非ケプラー軌道の理由とは考えにくいです。ディスノミアの非ケプラー軌道も引き起こされる可能性があります
衛星の非球形によって。海王星横断天体のケプラー/K2 光曲線に関する最近の研究 (Kecskeméthy
ら。 2022) は、TNO の光度曲線の振幅が残っていることを示しています。
メインの非球面性が大きい(D & 400 km)サイズで大きい
ベルトの小惑星は大幅に減少します (Vernazza et al. 2021)。その間
これは、より大きな領域での不規則から球状への遷移が原因である可能性があります
TNO のサイズ、それらの一般的な低密度と高気孔率
このシナリオに反対します。ディスノミアの予想サイズ
(D & 600 km) オブジェクトは、より高くても、かなり丸いはずです。
密度とかなりの内部強度。
巨人の中でエリス・ディスノミア系が形成されたと仮定すると
衝突後のエリスの回転期間は、おそらくはるかに短く、数時間程度でした。この高速回転は、ディスノミアとの潮汐相互作用によって減速されなければなりませんでした。上に示したように、同期回転に到達するには
期間ディスノミアは比較的大規模である必要があります(質量比の
q = 0.02-0.03)、Eris の Qp 潮汐消散係数と µp 剛性の正準値を仮定。この質量比は 2 番目の
〜8:1の比率の後の海王星以遠領域での最大値
冥王星・カロン系 (Barr & Schwamb 2016; Arakawa を参照)
ら。 2019;キス等。 2019、以前の評価の場合)。 (私たちは注意します
現在、Orcus-Vanth システムの質量比はむしろ
不明)。比較的高い質量比は、高いディスノミア密度 ρs = 1.8-2.4 g/ cm^3。
この中の海王星以遠天体の典型的な密度よりも大きい
サイズ範囲、ρ = 0.5-1.0 g/ cm^3
(例えば Bierson & Nimmo 2019 を参照)。
私たちの潮汐進化モデルでは、従来にない低い Qp 潮汐消散係数により、ディスノミア密度を低くすることができます(から ρs ≈ 1.2g cm−3) とエリスは で同期回転に達します
しかし同時に、これらの値は依然として R ≈ 300 km 天体の典型的な低密度を上回っており、
低レベルの気孔率。衝突シミュレーションは、
一般に、10−3 ≤ q ≤ 10−1 の無傷の衛星
で形成することができます
広範囲の影響パラメータを想定した海王星以遠領域 (Arakawa et al. 2019)。より詳細な影響と潮汐進化のシミュレーションにより、発生する条件を特定できるはずです。
現在の高密度エリス - 高密度ディスノミア系につながる可能性があります。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます