
Aegaeon の軌道と 7:6 Mimas-Aegaeon共鳴
Aegaeon (S/2008 S 1) は、カッシーニによって発見された最後の衛星です。
2000年代末の探査機。 衛星 Methone と Anthe のように、中型のミマスとの平均運動共鳴に関与しています。
この作業では、Aegaeon の現在の軌道の詳細な分析を行います。
ミマスによる共鳴的、長期的、長期的な摂動の特定
そして土星の偏平性、そしてテティスの影響。 このタスクのために、私たちは
の完全な運動方程式の数千の数値シミュレーションを実行します。
アイガイオンのクローンを表す小さな体の集合体。
7:6 Mimas-Aegaeon 共鳴のドメインをマッピングしました。
長半径と離心率の位相空間。 広い範囲を表示します
7:6 共回転共鳴に関連する規則的な運動によって支配される
混沌とした層に囲まれています。 アイガイオンは現在、
離心率まで伸びる共鳴の周期的軌道 ~ 0.025
長半径を中心に ~ 168,028 km。
Aegaeon の現在の軌道には、7:6 共鳴による離心率の重要な強制成分があることを示します。 の軌道傾斜角
Aegaeon は、長期的な摂動のために無視できない強制値を持っています。
ミマス。 これらの 2 つの強制モードは、複数の共鳴の共存を必要とせずに、Ae gaeon の複雑な摂動軌道を説明します。
キーワード 天体力学 · 自然衛星のダイナミクス · 土星系・アイガイオン。
1 はじめに
2000 年代を通して、カッシーニ探査機は新しい接近を発見しました。
衛星 Methone (S/2004 S 1; Porco 2004), Anthe (S/2007 S 4; Porco 2007),
アイガイオン (S/2008 S 1; ポルコ 2009)、再発見されたパレーネ (S/2004 S 2; ポルコ)
2004)、ボイジャーの画像ですでに検出されていた (Spitale et
アル。 2006)。 その後、これらの興味深い小さなオブジェクト(直径を持つ)の研究
10 km 未満) は、その起源に依存していました (例: Porco et al. 2007、Charnoz et al.
アル。 2010)、リング-サテライト相互作用と粒子の安定性 (e.g. Hedman et.
アル。 2009; マデイラら。 2018 年、Rodr´ıguez と Callegari 2021); 表面の特徴 (例: Hedman et al. 2010, Thomas and Helfenstein 2020); または共鳴
ダイナミクス、位相空間特性、および長期安定性 (Hedman et al. 2010,
エル・ムータミド等。 2014; Munōz-Guti´errez と Giuliatti-Winter 2017; カレガリとヨコヤマ 2010a, 2020; Callegari等。 2021; ロドリゲスら。 2022年、
提出 - この問題)。
この作業では、リストされている研究の後者のブランチを継続することを目指しています
アイガイオンの軌道ダイナミクスを詳細に研究することによって、上記のことがわかりました。 私たちの主な動機は、いわゆる「共回転」の調査に継続性を与えることです。
これは、臨界が存在する動的領域に対応します。
共鳴に関連付けられた角度は、近心の経度の周りに移動します
(またはアポセンターの)邪魔な体の。 土星系では、An the、Methone、および Aegaeon は現在、11:10 のドメインに閉じ込められています。
Anthe-Mimas、15:14 Methone-Mimas、および 7:6 Mimas-Aegaeon 平均運動
それぞれ共回転共鳴。 ミマスは摂動体なので、
直径がほぼ 400 km の中型の衛星で、上記の共鳴ペアの支配的な質量を表しています。 7:6 レゾナンスの場合、臨界角 σ2 = 7λM − 6λAe − $M は比較的小さい振幅 (Hedman et al. 2010)、下付き文字 M、Ae は Mimas を指す
それぞれとアイガイオン。 λ と $ は平均経度と経度
中心部の。
11:10 Anthe-Mimas のドメイン全体の数値マッピングと
15:14 メトン-ミマス共鳴は Callegari と
横山 (2020) と Callegari ら。 (2021)、それぞれ。 この作業では、
7:6 Mimas-Aegaeon 共鳴に完全に焦点を合わせます。 強調する価値があります
3つの共鳴はEl Moutamid らによって研究されています。 (2014)
平均モデルと断面曲面などの数値手法を採用することによって。
Munōz-Guti´errez と Giuliatti-Winter (2017) および Rodr´ıguez と Callegari
(2021) も 3 つの共鳴の位相空間を調査しましたが、彼らのアプローチには、周囲の粒子の集合体の動的寿命が含まれます。
アンテ、メトーネ、アイガイオン。
Aegaeon のダイナミクスに関する主な結果は、セクション 2 に記載されています。
ダイナミカル マップで得られた Aegaeon 位相空間のグローバル ビューは、セクション 2.1 で紹介されています。 共鳴のマッピングは数値的に行われました
アイガイオンの軌道を乱すいくつかの衛星を含むモデルで、
これは、7:6 レゾナンスの位相空間に関する以前の研究よりも一般的です (e.g. El Moutamid et al. 2014)。 の現在の軌道のクローズ ビュー
Aegaeon はセクション 2.2 に記載されています。 特に、現在の共鳴状態が共回転に関連する平衡解に非常に近いことを示します。
これは、σ2 の振動の振幅が小さい (~ 15 度) ことを説明しています。
セクション 2.2 と 2.3 では、主な重力摂動を分離します。
数値フーリエ解析によるアイガイオンの軌道。 それらは、共回転共振と強制共振成分の観点から物理的に解釈されます。
偏心と傾斜。
ヘドマン等。 (2010)は、関心のある他の7つの重要な議論を報告しました
共回転角に加えて、7:6 共鳴に関連する妨害機能。 これらの角度を ϕILR、ϕx、ϕy、ϕa、ϕb、ϕc、ϕd で参照します。 (表を参照
定義については、セクション 2.4 の 1。 この作業では、別の表記 (σi) を使用します。
別の方法論を採用して、我々はまた、
ヘドマンによって選択された物理的重要性を持つ批判的議論の同じセット
ら。 (2010)。 これらの角度はいずれも恒久的に解放されませんが、Hedman
ら。 (2010) は、アイガイオンの軌道に作用する複数の共鳴の観点から、それらの興味深い時間変動を説明しています。 前の 2 つの手順に従います。
Anthe と Methone に取り組んでいます (Callegari and Yokoyama 2020, Callegari et al.2021)、およびアイガイオンの軌道上の摂動成分を次のように解釈します。システムのいくつかの基本周波数の構成の結果
共回転共鳴と長期的な時間変化を含む
アイガイオンとミマスの軌道。 この議論はセクション2.4で与えられます。
ヘドマン等。 (2010) 初期値でアイガイオンの軌道を探索
そのエポックにおけるアイガイオンのベクトル状態のエラーの不確実性の範囲内で、
現在の軌道のすぐ近くは、数値シミュレーションで豊富な動的環境を示していると報告しています。 別の方法論を採用することによって (私たちは
エポックではなく、現在のものの周りの初期軌道要素を変更しました
ベクトル状態より)、初期のアイガイオン位相空間の証拠を与える
現在の近隣から比較的離れた場所にある条件は、他のことを明らかにします
物理的な関心領域。 位相空間のこれらの軌跡を D と S で表す
その中の軌道については、セクション 3.1 と 3.2 でそれぞれ調べます。
セクション 4 では、主要な結論といくつかの考察を示して論文を締めくくります。
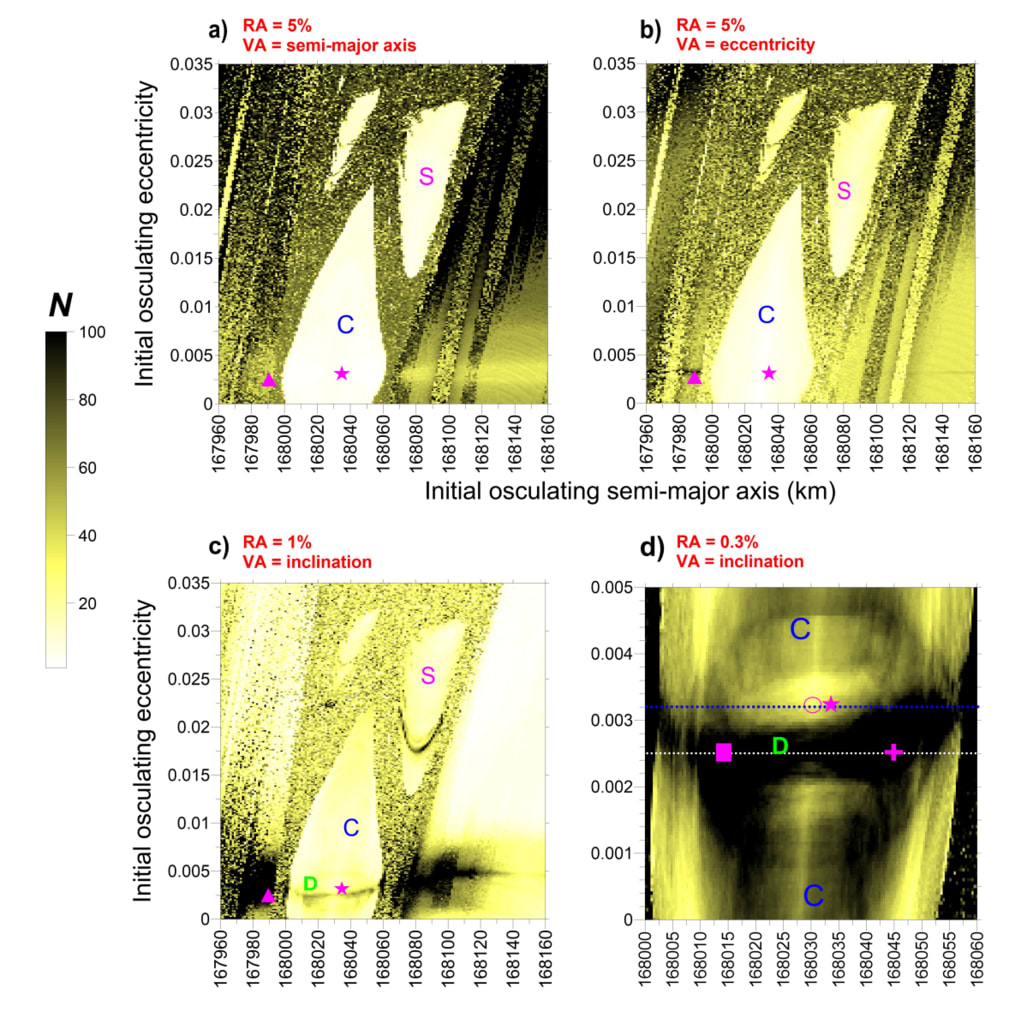
図 1 2016年 1月 1日の現在のアイガイオンの軌道周辺のダイナミック マッピング
ここで、a0 ~ 168、033.2 km、e0 ~ 0.0032 (マゼンタの星で表示)。 Cは共回転です
セクション 2.1 および 2.2 で検討したゾーン。 ブラック ストリップ D と領域 S は、それぞれ 3.1 節と 3.2 節で分析されます。 各初期条件の積分時間は 287.08 年で、0.1日のタイムステップ。 N は、セクション 2.1 で定義されたスペクトル数です。 (a,b,c): マップΔa = 1.25 km、Δe = 0.00014、および変数 (VA) で使用される基準振幅 RA
(a) 長半径 (RA=5%)、(b) 離心率 (RA=5%)、(c) 傾斜 (RA=1%) です。
(a) の三角形のマゼンタ シンボルには、初期条件 (a0, e0) = (167, 990, 0.0025) があります。 (d):(c) の下部に詳細があり、合計 15,251 の初期条件が統合されています。
RAは0.3%です。 マゼンタの記号は異なる (a0、e0) に対応します。 正方形: (168, 014, 0.0025);核心部 (168, 045, 0.0025); 白丸 (168, 030, 0.0032)。

図 2 上段: 構築された 1500 個の Aegaeon クローンの個々のパワー スペクトル (IPS)
プロットの上部に示されているさまざまな変数のスペクトルから。 Pσ2
は、7:6 Mimas-Aegaeon 共回転共鳴に対応する周期です。 P42~26、214.4が関連
Mimas-Tethys 4:2 共鳴に。 P∆$、P∆Ω: ターベーションごとの相互経年長期 Mimas-Aegaeon。 H1 と H2 は高調波です。 下の行: 最初の半長軸に対応する軌道の個々のスペクトルは、上の行の垂直の破線で示されます。
2016年 1月 1日のアイガイオンの現在値と同様です。積分時間は 1720年です。
タイム ステップ 0.12 日。 主な時期の概算値は、
ピーク。 長半径のスペクトルの x 軸は、対数スケールで表示されます。

図 3 幾何軌道要素の時間変化と軌道のいくつかの重要な引数
Aegaeon に似た衛星の数値シミュレーションから得られた擾乱関数。
ダイナミクスの解釈を明確にするために、プロットの x 軸を以下に示します。
プロットに応じて 2 つの異なるスケール。 括弧内に角度の表記を示します
Hedmanらによって報告されたように。 (2010)。 定義については、表 1 およびセクション 2 を参照してください。 初期
条件は、2016 年 1 月 1 日の天体暦の Horizons システムから取得されました。
付録に記載されています。 シミュレーションには、Aegaeon と中型衛星が含まれます。
タイタンまで、土星のJ2とJ4まで。 水平方向の矢印は、主な運動体制を示しています
RM: 共振モード。 MS-LT-ecc: 相互世俗的長期
偏心のモード; MS-LT-incl: 傾斜における相互長期モード
Aegaeon (S/2008 S 1) は、カッシーニによって発見された最後の衛星です。
2000年代末の探査機。 衛星 Methone と Anthe のように、中型のミマスとの平均運動共鳴に関与しています。
この作業では、Aegaeon の現在の軌道の詳細な分析を行います。
ミマスによる共鳴的、長期的、長期的な摂動の特定
そして土星の偏平性、そしてテティスの影響。 このタスクのために、私たちは
の完全な運動方程式の数千の数値シミュレーションを実行します。
アイガイオンのクローンを表す小さな体の集合体。
7:6 Mimas-Aegaeon 共鳴のドメインをマッピングしました。
長半径と離心率の位相空間。 広い範囲を表示します
7:6 共回転共鳴に関連する規則的な運動によって支配される
混沌とした層に囲まれています。 アイガイオンは現在、
離心率まで伸びる共鳴の周期的軌道 ~ 0.025
長半径を中心に ~ 168,028 km。
Aegaeon の現在の軌道には、7:6 共鳴による離心率の重要な強制成分があることを示します。 の軌道傾斜角
Aegaeon は、長期的な摂動のために無視できない強制値を持っています。
ミマス。 これらの 2 つの強制モードは、複数の共鳴の共存を必要とせずに、Ae gaeon の複雑な摂動軌道を説明します。
キーワード 天体力学 · 自然衛星のダイナミクス · 土星系・アイガイオン。
1 はじめに
2000 年代を通して、カッシーニ探査機は新しい接近を発見しました。
衛星 Methone (S/2004 S 1; Porco 2004), Anthe (S/2007 S 4; Porco 2007),
アイガイオン (S/2008 S 1; ポルコ 2009)、再発見されたパレーネ (S/2004 S 2; ポルコ)
2004)、ボイジャーの画像ですでに検出されていた (Spitale et
アル。 2006)。 その後、これらの興味深い小さなオブジェクト(直径を持つ)の研究
10 km 未満) は、その起源に依存していました (例: Porco et al. 2007、Charnoz et al.
アル。 2010)、リング-サテライト相互作用と粒子の安定性 (e.g. Hedman et.
アル。 2009; マデイラら。 2018 年、Rodr´ıguez と Callegari 2021); 表面の特徴 (例: Hedman et al. 2010, Thomas and Helfenstein 2020); または共鳴
ダイナミクス、位相空間特性、および長期安定性 (Hedman et al. 2010,
エル・ムータミド等。 2014; Munōz-Guti´errez と Giuliatti-Winter 2017; カレガリとヨコヤマ 2010a, 2020; Callegari等。 2021; ロドリゲスら。 2022年、
提出 - この問題)。
この作業では、リストされている研究の後者のブランチを継続することを目指しています
アイガイオンの軌道ダイナミクスを詳細に研究することによって、上記のことがわかりました。 私たちの主な動機は、いわゆる「共回転」の調査に継続性を与えることです。
これは、臨界が存在する動的領域に対応します。
共鳴に関連付けられた角度は、近心の経度の周りに移動します
(またはアポセンターの)邪魔な体の。 土星系では、An the、Methone、および Aegaeon は現在、11:10 のドメインに閉じ込められています。
Anthe-Mimas、15:14 Methone-Mimas、および 7:6 Mimas-Aegaeon 平均運動
それぞれ共回転共鳴。 ミマスは摂動体なので、
直径がほぼ 400 km の中型の衛星で、上記の共鳴ペアの支配的な質量を表しています。 7:6 レゾナンスの場合、臨界角 σ2 = 7λM − 6λAe − $M は比較的小さい振幅 (Hedman et al. 2010)、下付き文字 M、Ae は Mimas を指す
それぞれとアイガイオン。 λ と $ は平均経度と経度
中心部の。
11:10 Anthe-Mimas のドメイン全体の数値マッピングと
15:14 メトン-ミマス共鳴は Callegari と
横山 (2020) と Callegari ら。 (2021)、それぞれ。 この作業では、
7:6 Mimas-Aegaeon 共鳴に完全に焦点を合わせます。 強調する価値があります
3つの共鳴はEl Moutamid らによって研究されています。 (2014)
平均モデルと断面曲面などの数値手法を採用することによって。
Munōz-Guti´errez と Giuliatti-Winter (2017) および Rodr´ıguez と Callegari
(2021) も 3 つの共鳴の位相空間を調査しましたが、彼らのアプローチには、周囲の粒子の集合体の動的寿命が含まれます。
アンテ、メトーネ、アイガイオン。
Aegaeon のダイナミクスに関する主な結果は、セクション 2 に記載されています。
ダイナミカル マップで得られた Aegaeon 位相空間のグローバル ビューは、セクション 2.1 で紹介されています。 共鳴のマッピングは数値的に行われました
アイガイオンの軌道を乱すいくつかの衛星を含むモデルで、
これは、7:6 レゾナンスの位相空間に関する以前の研究よりも一般的です (e.g. El Moutamid et al. 2014)。 の現在の軌道のクローズ ビュー
Aegaeon はセクション 2.2 に記載されています。 特に、現在の共鳴状態が共回転に関連する平衡解に非常に近いことを示します。
これは、σ2 の振動の振幅が小さい (~ 15 度) ことを説明しています。
セクション 2.2 と 2.3 では、主な重力摂動を分離します。
数値フーリエ解析によるアイガイオンの軌道。 それらは、共回転共振と強制共振成分の観点から物理的に解釈されます。
偏心と傾斜。
ヘドマン等。 (2010)は、関心のある他の7つの重要な議論を報告しました
共回転角に加えて、7:6 共鳴に関連する妨害機能。 これらの角度を ϕILR、ϕx、ϕy、ϕa、ϕb、ϕc、ϕd で参照します。 (表を参照
定義については、セクション 2.4 の 1。 この作業では、別の表記 (σi) を使用します。
別の方法論を採用して、我々はまた、
ヘドマンによって選択された物理的重要性を持つ批判的議論の同じセット
ら。 (2010)。 これらの角度はいずれも恒久的に解放されませんが、Hedman
ら。 (2010) は、アイガイオンの軌道に作用する複数の共鳴の観点から、それらの興味深い時間変動を説明しています。 前の 2 つの手順に従います。
Anthe と Methone に取り組んでいます (Callegari and Yokoyama 2020, Callegari et al.2021)、およびアイガイオンの軌道上の摂動成分を次のように解釈します。システムのいくつかの基本周波数の構成の結果
共回転共鳴と長期的な時間変化を含む
アイガイオンとミマスの軌道。 この議論はセクション2.4で与えられます。
ヘドマン等。 (2010) 初期値でアイガイオンの軌道を探索
そのエポックにおけるアイガイオンのベクトル状態のエラーの不確実性の範囲内で、
現在の軌道のすぐ近くは、数値シミュレーションで豊富な動的環境を示していると報告しています。 別の方法論を採用することによって (私たちは
エポックではなく、現在のものの周りの初期軌道要素を変更しました
ベクトル状態より)、初期のアイガイオン位相空間の証拠を与える
現在の近隣から比較的離れた場所にある条件は、他のことを明らかにします
物理的な関心領域。 位相空間のこれらの軌跡を D と S で表す
その中の軌道については、セクション 3.1 と 3.2 でそれぞれ調べます。
セクション 4 では、主要な結論といくつかの考察を示して論文を締めくくります。

図 1 2016年 1月 1日の現在のアイガイオンの軌道周辺のダイナミック マッピング
ここで、a0 ~ 168、033.2 km、e0 ~ 0.0032 (マゼンタの星で表示)。 Cは共回転です
セクション 2.1 および 2.2 で検討したゾーン。 ブラック ストリップ D と領域 S は、それぞれ 3.1 節と 3.2 節で分析されます。 各初期条件の積分時間は 287.08 年で、0.1日のタイムステップ。 N は、セクション 2.1 で定義されたスペクトル数です。 (a,b,c): マップΔa = 1.25 km、Δe = 0.00014、および変数 (VA) で使用される基準振幅 RA
(a) 長半径 (RA=5%)、(b) 離心率 (RA=5%)、(c) 傾斜 (RA=1%) です。
(a) の三角形のマゼンタ シンボルには、初期条件 (a0, e0) = (167, 990, 0.0025) があります。 (d):(c) の下部に詳細があり、合計 15,251 の初期条件が統合されています。
RAは0.3%です。 マゼンタの記号は異なる (a0、e0) に対応します。 正方形: (168, 014, 0.0025);核心部 (168, 045, 0.0025); 白丸 (168, 030, 0.0032)。

図 2 上段: 構築された 1500 個の Aegaeon クローンの個々のパワー スペクトル (IPS)
プロットの上部に示されているさまざまな変数のスペクトルから。 Pσ2
は、7:6 Mimas-Aegaeon 共回転共鳴に対応する周期です。 P42~26、214.4が関連
Mimas-Tethys 4:2 共鳴に。 P∆$、P∆Ω: ターベーションごとの相互経年長期 Mimas-Aegaeon。 H1 と H2 は高調波です。 下の行: 最初の半長軸に対応する軌道の個々のスペクトルは、上の行の垂直の破線で示されます。
2016年 1月 1日のアイガイオンの現在値と同様です。積分時間は 1720年です。
タイム ステップ 0.12 日。 主な時期の概算値は、
ピーク。 長半径のスペクトルの x 軸は、対数スケールで表示されます。

図 3 幾何軌道要素の時間変化と軌道のいくつかの重要な引数
Aegaeon に似た衛星の数値シミュレーションから得られた擾乱関数。
ダイナミクスの解釈を明確にするために、プロットの x 軸を以下に示します。
プロットに応じて 2 つの異なるスケール。 括弧内に角度の表記を示します
Hedmanらによって報告されたように。 (2010)。 定義については、表 1 およびセクション 2 を参照してください。 初期
条件は、2016 年 1 月 1 日の天体暦の Horizons システムから取得されました。
付録に記載されています。 シミュレーションには、Aegaeon と中型衛星が含まれます。
タイタンまで、土星のJ2とJ4まで。 水平方向の矢印は、主な運動体制を示しています
RM: 共振モード。 MS-LT-ecc: 相互世俗的長期
偏心のモード; MS-LT-incl: 傾斜における相互長期モード
4 結論と考察
Hedman et al. で最初に報告された Aegaeon のダイナミックな環境の豊かさに動機付けられました。(2010)この作業では、現在の軌道を研究しています
非線形システムの拡張データと技術を備えたこの小さな衛星。
衛星の何千ものクローンの数値積分を実行しました
現在の軌道のすぐ近くにあるため、詳細な調査を行うことができます
7:6 Mimas-Aegaeon 共鳴の位相空間の。 この共鳴は
共回転角 σ2 が π 付近で変化することをよく特徴とします。
つまり、ミマスとアイガイオンの結合が一列に並んでいるということです。
は常にミマスのアポセンターの経度を中心に振動しています。
循環と振動の間の異常な遷移を説明します
リンドブラッド角の σ1 = 7λM − 6λAe − $Ae (Hedman et al. の ϕLER
2010)、および角度 σ3 (ϕx)、σ4 (ϕy)、σ7 (ϕb)、σ8 (ϕa) を図 3 に示します。
これらの角度の運動体制の交替は、
アイガイオンの軌道の離心率における強制成分の結果
共鳴し、角度 ∆$M−Ae = $M −$Ae はエピソード的に振動する
π付近。 強制偏心は ef ~ 0.0002 で、同様の大きさです。
Hedmanらで推測されたように、自由な偏心に。 (2010)。
σ11 (ϕc) と σ10 (ϕd) の場合、経度の相対運動
Mimas と Aegaeon の昇交点の ∆ΩM−Ae = ΩM − ΩAe が再生されます。
重要な役割です (Hedman et al. 2010)。 特に、我々はそれを示しました
このシノドス角 ΔΩM−Ae は、ゼロ付近で一時的に振動する可能性があります。 相対昇順ノードのこの異常な変動を、
Aegaeon の軌道の傾きの強制成分が ~ 0.001 度の場合、
日付に対する現在の幾何学的傾きと同様の値を使用して、
傾きが非常に小さい。 軌道の強制値は注目に値します
アイガイオンの傾きはミマスとの長期的な摂動によるものであり、
7:6レゾナンス。
アイガイオンの軌道の摂動に関する私たちの解釈は、
で数値的に決定された後、基本周波数について
スペクトル分析は、共鳴、永年、および
主にMimasとJ2による長期摂動。 必須ではありません
アイガイオンの軌道で作用する複数の共鳴の共存
この場合、現在の軌道におけるカオス運動の潜在的な信号です。 さらに、私たちは
主な摂動はミマスによるものであることが示されています。
土星の重力場、および寄与が弱いテティス。
同様の結果が Anthe およびメトンも、それぞれの内部に非常に規則的な軌道を閉じ込めています。
Mimas との共回転共鳴 (Callegari and Yokoyama 2020、Calle gari et al. 2021、およびその中の参考文献を参照)。 ただし、複雑なため、
一見、アイガイオンの軌道に作用する共鳴摂動は、
これにより、Mimas との 7:6 の共鳴が、Anthe の共鳴とは異なるものになります。
方法ですが、そうではありません。 実際、共回転ゾーンは
位相空間、離心率〜0.025に達し、半長軸はで与えられます
数値で決定できるように、間隔は〜168,000〜168,060 kmです。
位相空間のマッピング。 を区別する唯一の主な違い
Mimas-Aegaeon の場合は強制傾斜です。 軌道の個別分析
Dの領域(図1a、b)では、下部にマッピングされた「不安定性」が示されています
共回転ゾーンの一部は、傾斜のこの強制成分に関連しています。
テスト衛星の。 図1b、cに示すマップはこれを確認します。
変数は長半径と離心率であり、暗い領域はそうではありません
現在。
と比較した場合のミマス-アイガイオン共鳴の重要な特徴
他の 2 つの共回転共鳴は、アイガイオンの近くにあります。
7:6 共鳴の中心への軌道、Hedman etアル。 (2010) であり、周期的な遺伝子座の数値マッピングで確認されました
共回転共鳴に関連する軌道(図1dを参照)。 ヘドマン等。 (2010)
アイガイオンとその地域の他の天体との相互作用を推測
その現在の軌道構成を説明します(アイガイオンはアークに浸っています
Gリング内)。
アイガイオンとその周辺の現在の軌道から遠く離れたところに、
の分離を取り巻く規則的な動きのレジームの存在 7:6 共回転ゾーン。 同様の動きのレジームがすでに行われています
Callegari and Yokoyama (2010a) は、衛星パレーネの場合です。 意味がない
運動共鳴はそれらのサイトに関連付けられており、個々の検査
S領域の内部の軌道は、の平衡配置を明らかにします
経年角 θ = Δ$M−s + ΔΩM−s (試験衛星の場合は s)
軌道面の傾きに。
Hedman et al. で最初に報告された Aegaeon のダイナミックな環境の豊かさに動機付けられました。(2010)この作業では、現在の軌道を研究しています
非線形システムの拡張データと技術を備えたこの小さな衛星。
衛星の何千ものクローンの数値積分を実行しました
現在の軌道のすぐ近くにあるため、詳細な調査を行うことができます
7:6 Mimas-Aegaeon 共鳴の位相空間の。 この共鳴は
共回転角 σ2 が π 付近で変化することをよく特徴とします。
つまり、ミマスとアイガイオンの結合が一列に並んでいるということです。
は常にミマスのアポセンターの経度を中心に振動しています。
循環と振動の間の異常な遷移を説明します
リンドブラッド角の σ1 = 7λM − 6λAe − $Ae (Hedman et al. の ϕLER
2010)、および角度 σ3 (ϕx)、σ4 (ϕy)、σ7 (ϕb)、σ8 (ϕa) を図 3 に示します。
これらの角度の運動体制の交替は、
アイガイオンの軌道の離心率における強制成分の結果
共鳴し、角度 ∆$M−Ae = $M −$Ae はエピソード的に振動する
π付近。 強制偏心は ef ~ 0.0002 で、同様の大きさです。
Hedmanらで推測されたように、自由な偏心に。 (2010)。
σ11 (ϕc) と σ10 (ϕd) の場合、経度の相対運動
Mimas と Aegaeon の昇交点の ∆ΩM−Ae = ΩM − ΩAe が再生されます。
重要な役割です (Hedman et al. 2010)。 特に、我々はそれを示しました
このシノドス角 ΔΩM−Ae は、ゼロ付近で一時的に振動する可能性があります。 相対昇順ノードのこの異常な変動を、
Aegaeon の軌道の傾きの強制成分が ~ 0.001 度の場合、
日付に対する現在の幾何学的傾きと同様の値を使用して、
傾きが非常に小さい。 軌道の強制値は注目に値します
アイガイオンの傾きはミマスとの長期的な摂動によるものであり、
7:6レゾナンス。
アイガイオンの軌道の摂動に関する私たちの解釈は、
で数値的に決定された後、基本周波数について
スペクトル分析は、共鳴、永年、および
主にMimasとJ2による長期摂動。 必須ではありません
アイガイオンの軌道で作用する複数の共鳴の共存
この場合、現在の軌道におけるカオス運動の潜在的な信号です。 さらに、私たちは
主な摂動はミマスによるものであることが示されています。
土星の重力場、および寄与が弱いテティス。
同様の結果が Anthe およびメトンも、それぞれの内部に非常に規則的な軌道を閉じ込めています。
Mimas との共回転共鳴 (Callegari and Yokoyama 2020、Calle gari et al. 2021、およびその中の参考文献を参照)。 ただし、複雑なため、
一見、アイガイオンの軌道に作用する共鳴摂動は、
これにより、Mimas との 7:6 の共鳴が、Anthe の共鳴とは異なるものになります。
方法ですが、そうではありません。 実際、共回転ゾーンは
位相空間、離心率〜0.025に達し、半長軸はで与えられます
数値で決定できるように、間隔は〜168,000〜168,060 kmです。
位相空間のマッピング。 を区別する唯一の主な違い
Mimas-Aegaeon の場合は強制傾斜です。 軌道の個別分析
Dの領域(図1a、b)では、下部にマッピングされた「不安定性」が示されています
共回転ゾーンの一部は、傾斜のこの強制成分に関連しています。
テスト衛星の。 図1b、cに示すマップはこれを確認します。
変数は長半径と離心率であり、暗い領域はそうではありません
現在。
と比較した場合のミマス-アイガイオン共鳴の重要な特徴
他の 2 つの共回転共鳴は、アイガイオンの近くにあります。
7:6 共鳴の中心への軌道、Hedman etアル。 (2010) であり、周期的な遺伝子座の数値マッピングで確認されました
共回転共鳴に関連する軌道(図1dを参照)。 ヘドマン等。 (2010)
アイガイオンとその地域の他の天体との相互作用を推測
その現在の軌道構成を説明します(アイガイオンはアークに浸っています
Gリング内)。
アイガイオンとその周辺の現在の軌道から遠く離れたところに、
の分離を取り巻く規則的な動きのレジームの存在 7:6 共回転ゾーン。 同様の動きのレジームがすでに行われています
Callegari and Yokoyama (2010a) は、衛星パレーネの場合です。 意味がない
運動共鳴はそれらのサイトに関連付けられており、個々の検査
S領域の内部の軌道は、の平衡配置を明らかにします
経年角 θ = Δ$M−s + ΔΩM−s (試験衛星の場合は s)
軌道面の傾きに。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます