
ジュノ重力と時変磁場測定を組み合わせた木星のディープジェットの解析
K2019年6月19日に提出された)
木星の内部の流れの構造はまだ完全には知られていませんが、Junoの高精度測定のおかげで今までよりよく束縛されることができます。最近発表された重力と磁場の測定は、惑星とその内部の流れに関する新しい情報をもたらしました、そして将来の磁気測定はこのパズルを解決することにおいて別の一歩を踏み出すことを可能にするでしょう。本研究では、磁気永年変化の予想される測定値と組み合わせたJuno重力測定値を使用して、木星の内部流れ場をよりよく拘束するための新しい方法を提案します。流体力学的および磁場的考察の組み合わせに基づいて、我々は両方の測定値に適合する帯状流の最適化された垂直プロファイルが得られることを示す。流れへの磁場の影響を取り入れることは、流れの減衰プロファイルをより良く拘束する。
図1:Kaspi et al。の減衰プロファイル。 (2018)(黒)、∂Bの生成に使用された擬似減衰プロファイル
∂t
測定値(青)、電気伝導度(赤破線)、およびLiuに表示される電気伝導度
他。 線形(a)および対数目盛(b)では、2008(淡い赤色の破線)。
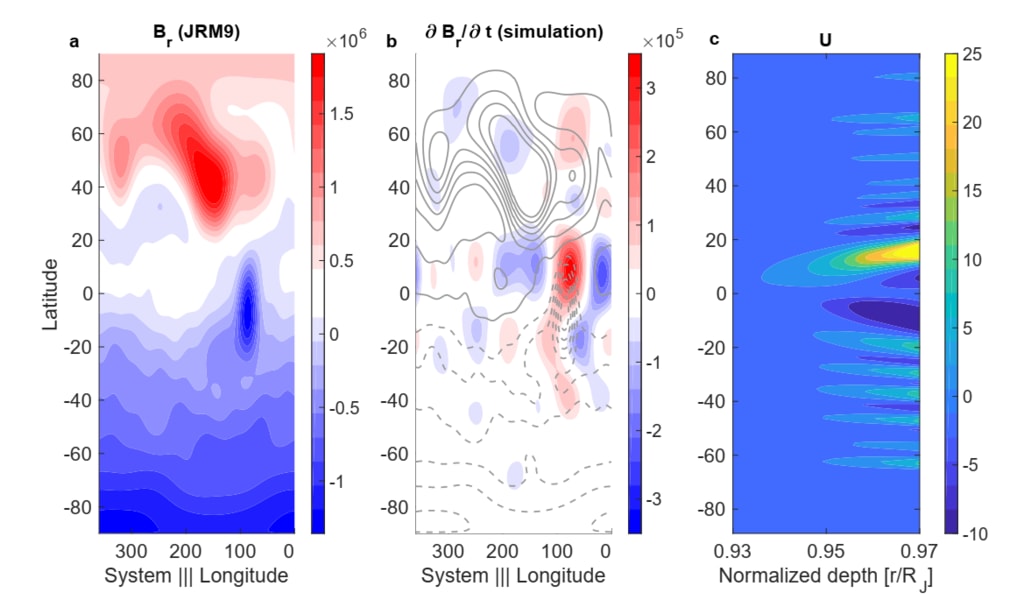
図2:(a)Junoの最初の9つの軌道(JRM9)から約0.972RJで測定された磁場[nT](Connerney)
ら、2018)(b)磁場の変化[nT・yr-1]
]で1年後にシミュレートされたプロファイルによる 灰色の等高線は測定された磁場(JRM9)と(c)シミュレートされた帯状流を示す。
緯度と深度の関数[ms − 1]深さ0.97 RJと0.93 RJの間。 (a)と(b)の両方が表されます
ここでは、Connerney et al。のようにわずか10度で次数の磁気調和係数がある。 (2018)。

図3:(a)下部の誘導モデル解と一緒にシミュレートされた減衰プロファイル(黒い破線)
領域(緑)、その3σの不確定性(緑の点線)、と組み合わせた上部領域のTWモデル解
RT以下の誘導ソリューション(赤)と組み合わせたソリューションの追加オプション(赤破線)。 また
示されているのは、0.972 RJでの誘導モデルの境界(灰色の破線)です。 帰納モデルの解は非常に
導電率が高い地域では、〜3000 km以下で良好です。 (b)帰納法の費用関数マップ
2つの最適化されたパラメータの関数としてのモデル:指数減衰率(HM)と
表面流(UM)に対する誘導モデルの上限。 モデルの最適解も表示されます(赤
そしてそれからO(1)内のすべての解(ピンク)。

図4:重力と磁気を組み合わせた解 (a)Br [nT・yr − 1]における時間変化] から
シミュレーション、(b)Br [nT・yr − 1]の変化に対するモデル解]同じ期間後、そして(c)重力
Juno(赤)によって測定され、モデルの最良解の結果から計算された異常(青)。
K2019年6月19日に提出された)
木星の内部の流れの構造はまだ完全には知られていませんが、Junoの高精度測定のおかげで今までよりよく束縛されることができます。最近発表された重力と磁場の測定は、惑星とその内部の流れに関する新しい情報をもたらしました、そして将来の磁気測定はこのパズルを解決することにおいて別の一歩を踏み出すことを可能にするでしょう。本研究では、磁気永年変化の予想される測定値と組み合わせたJuno重力測定値を使用して、木星の内部流れ場をよりよく拘束するための新しい方法を提案します。流体力学的および磁場的考察の組み合わせに基づいて、我々は両方の測定値に適合する帯状流の最適化された垂直プロファイルが得られることを示す。流れへの磁場の影響を取り入れることは、流れの減衰プロファイルをより良く拘束する。
図1:Kaspi et al。の減衰プロファイル。 (2018)(黒)、∂Bの生成に使用された擬似減衰プロファイル
∂t
測定値(青)、電気伝導度(赤破線)、およびLiuに表示される電気伝導度
他。 線形(a)および対数目盛(b)では、2008(淡い赤色の破線)。

図2:(a)Junoの最初の9つの軌道(JRM9)から約0.972RJで測定された磁場[nT](Connerney)
ら、2018)(b)磁場の変化[nT・yr-1]
]で1年後にシミュレートされたプロファイルによる 灰色の等高線は測定された磁場(JRM9)と(c)シミュレートされた帯状流を示す。
緯度と深度の関数[ms − 1]深さ0.97 RJと0.93 RJの間。 (a)と(b)の両方が表されます
ここでは、Connerney et al。のようにわずか10度で次数の磁気調和係数がある。 (2018)。

図3:(a)下部の誘導モデル解と一緒にシミュレートされた減衰プロファイル(黒い破線)
領域(緑)、その3σの不確定性(緑の点線)、と組み合わせた上部領域のTWモデル解
RT以下の誘導ソリューション(赤)と組み合わせたソリューションの追加オプション(赤破線)。 また
示されているのは、0.972 RJでの誘導モデルの境界(灰色の破線)です。 帰納モデルの解は非常に
導電率が高い地域では、〜3000 km以下で良好です。 (b)帰納法の費用関数マップ
2つの最適化されたパラメータの関数としてのモデル:指数減衰率(HM)と
表面流(UM)に対する誘導モデルの上限。 モデルの最適解も表示されます(赤
そしてそれからO(1)内のすべての解(ピンク)。

図4:重力と磁気を組み合わせた解 (a)Br [nT・yr − 1]における時間変化] から
シミュレーション、(b)Br [nT・yr − 1]の変化に対するモデル解]同じ期間後、そして(c)重力
Juno(赤)によって測定され、モデルの最良解の結果から計算された異常(青)。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます