エンケラドスの極から赤道にかけての海の逆転循環
2020年7月13日に提出
エンケラドスは、平均深さが30〜kmの海水全球海を持ち、海とコアの境界面で下から加熱され、上部で冷却され、海は上の氷河リソスフェアに熱を失います。このシナリオは、エンケラドスの海の内部特性と循環に影響を与える垂直対流の重要な役割を示唆しています。さらに、海を取り巻く氷の殻には、子午線方向の厚みに劇的な変化があり、定常状態では、これらの氷の厚みの異常を取り除くために作用するプロセスに対して維持する必要があります。氷の殻の厚さの変動を維持するメカニズムの1つは、海と氷の境界面で空間的に分離された氷結と融解の領域を含みます。ここでは、理想化された、エンケラドスの内部の海は子午線の転覆循環をサポートする必要があると主張するために、海洋と氷の境界に観測的に誘導された密度強制によって強制される動的海洋モデル。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。
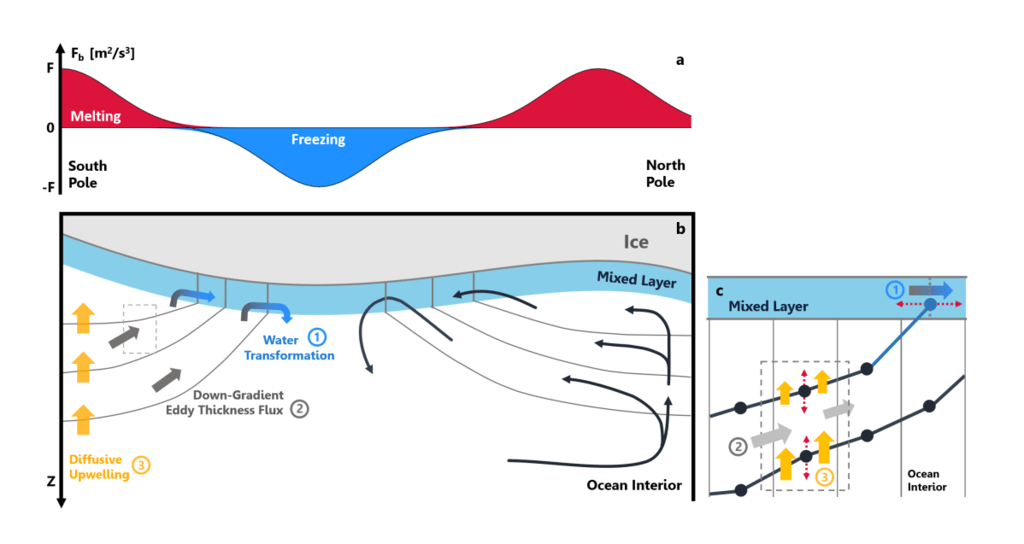
図1:エンケラドスのような海と循環の図。 (a)推定された表面浮力の強制(Fb、m2 / s3)、
パネル(b)に示す測定された子午面氷厚勾配に基づく。 (b)海洋内部の概略図
密度の異なるレイヤーに分割されます(灰色の線)。 右側は全体の概略図です
循環を覆す一方で、左側はこの循環をサポートする物理的なプロセスを示しています。
パネル(c)の挿入図は、物理プロセスがモデルグリッド内でどのように表現されるかを示しています。 ダークブルー
ドットは、時間とともに変化する各レイヤーの深さを示します。 インターフェースが露出している位置
海洋と氷の境界(水色の点)も、グリッドとは無関係に、時間とともに変化します。 この図は描かれていません
規模。 以下で説明するシミュレーションは、単純化された氷の勾配を使用して、南半球にのみ焦点を当てています(図。 2)表面浮力の強制(S.1図s1を参照)

図2:制御実行における密度層の定常分布。 上部パネルには、
傾斜した海と氷の界面に関して層の界面。 下のパネルには同じレイヤーがプロットされて表示されています
層の厚さの勾配をより簡単に視覚化するために、海洋と氷の境界の下の深さとして。

図3:制御シミュレーションの特性。 (a)5つの密度層のそれぞれの厚さ(m)
緯度の関数。赤道に向かって移動する層の厚さの減少は、赤道をサポートします
各層内の渦輸送。 (b)体積輸送(1 Sv = 106 m3s−1)統合された密度曲面
極から北へ、suchDiabatic(φ)= Rφ−90 w2πRcos(φ0)dφ0、ここでφ0
積分変数です。
正の値は、密度の高い層から軽い層への体積フラックスを示します。定常状態では、非断熱輸送
極と緯度φの間に統合された特定のインターフェイス全体で、総断熱によってバランスをとる必要があります
interfaceDiabatic =ΨAdiabatic= Ke(s − sice)2πcosφであるような、その境界の上の横輸送。黒い
70◦の破線
緯度は、図4で横方向のフラックスが計算される場所を示します。 4. y軸は
最深層(5)が下部に表示され、最薄層(1)が
上。どちらのパネルでも、レイヤー番号と色は図1と同じです。 2。

図4:さまざまなモデルパラメーターの等密度勾配を示す相図。 上から下に示します
φbrineを変化させた結果(◦緯度)、F(m2s−3)、Ke(m2s−1)、κ(m2s−1)。 左側のパネルでは、
縦軸は南極での各層界面の深さ(km)を示し、横軸は
インターフェース露頭位置の緯度。 各モデルの5つの露頭は、
同じ色。 背景色は、一定の等密度勾配の線を示します。 右側のパネルは側面を示しています
体積流束(1 Sv = 106 m3s−1)70◦の各レイヤー内
緯度。 パネル(g)では、
灰色は、ダイアプシナル混合κの極増幅が削除されたコントロールのようなシミュレーション用です。
2020年7月13日に提出
エンケラドスは、平均深さが30〜kmの海水全球海を持ち、海とコアの境界面で下から加熱され、上部で冷却され、海は上の氷河リソスフェアに熱を失います。このシナリオは、エンケラドスの海の内部特性と循環に影響を与える垂直対流の重要な役割を示唆しています。さらに、海を取り巻く氷の殻には、子午線方向の厚みに劇的な変化があり、定常状態では、これらの氷の厚みの異常を取り除くために作用するプロセスに対して維持する必要があります。氷の殻の厚さの変動を維持するメカニズムの1つは、海と氷の境界面で空間的に分離された氷結と融解の領域を含みます。ここでは、理想化された、エンケラドスの内部の海は子午線の転覆循環をサポートする必要があると主張するために、海洋と氷の境界に観測的に誘導された密度強制によって強制される動的海洋モデル。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。この循環は、極域の浅い淡水レンズを含む対流のみに焦点を当てた研究よりも複雑な内部密度構造を確立します。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。氷の形成とメルトの空間的に分離されたサイトは、エンケラドスが重要な垂直および水平の成層を維持できるようにします。極海と氷の境界付近の低塩分層の存在も、プルームから測定されたサンプルが地球規模の海洋を代表するものであるかどうかに影響を与えます。
図1:エンケラドスのような海と循環の図。 (a)推定された表面浮力の強制(Fb、m2 / s3)、
パネル(b)に示す測定された子午面氷厚勾配に基づく。 (b)海洋内部の概略図
密度の異なるレイヤーに分割されます(灰色の線)。 右側は全体の概略図です
循環を覆す一方で、左側はこの循環をサポートする物理的なプロセスを示しています。
パネル(c)の挿入図は、物理プロセスがモデルグリッド内でどのように表現されるかを示しています。 ダークブルー
ドットは、時間とともに変化する各レイヤーの深さを示します。 インターフェースが露出している位置
海洋と氷の境界(水色の点)も、グリッドとは無関係に、時間とともに変化します。 この図は描かれていません
規模。 以下で説明するシミュレーションは、単純化された氷の勾配を使用して、南半球にのみ焦点を当てています(図。 2)表面浮力の強制(S.1図s1を参照)

図2:制御実行における密度層の定常分布。 上部パネルには、
傾斜した海と氷の界面に関して層の界面。 下のパネルには同じレイヤーがプロットされて表示されています
層の厚さの勾配をより簡単に視覚化するために、海洋と氷の境界の下の深さとして。

図3:制御シミュレーションの特性。 (a)5つの密度層のそれぞれの厚さ(m)
緯度の関数。赤道に向かって移動する層の厚さの減少は、赤道をサポートします
各層内の渦輸送。 (b)体積輸送(1 Sv = 106 m3s−1)統合された密度曲面
極から北へ、suchDiabatic(φ)= Rφ−90 w2πRcos(φ0)dφ0、ここでφ0
積分変数です。
正の値は、密度の高い層から軽い層への体積フラックスを示します。定常状態では、非断熱輸送
極と緯度φの間に統合された特定のインターフェイス全体で、総断熱によってバランスをとる必要があります
interfaceDiabatic =ΨAdiabatic= Ke(s − sice)2πcosφであるような、その境界の上の横輸送。黒い
70◦の破線
緯度は、図4で横方向のフラックスが計算される場所を示します。 4. y軸は
最深層(5)が下部に表示され、最薄層(1)が
上。どちらのパネルでも、レイヤー番号と色は図1と同じです。 2。

図4:さまざまなモデルパラメーターの等密度勾配を示す相図。 上から下に示します
φbrineを変化させた結果(◦緯度)、F(m2s−3)、Ke(m2s−1)、κ(m2s−1)。 左側のパネルでは、
縦軸は南極での各層界面の深さ(km)を示し、横軸は
インターフェース露頭位置の緯度。 各モデルの5つの露頭は、
同じ色。 背景色は、一定の等密度勾配の線を示します。 右側のパネルは側面を示しています
体積流束(1 Sv = 106 m3s−1)70◦の各レイヤー内
緯度。 パネル(g)では、
灰色は、ダイアプシナル混合κの極増幅が削除されたコントロールのようなシミュレーション用です。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます