
惑星探査の場合は金星、地球と木星を使うことが多いが、NEOやメインベルトの小惑星探査の場合、月と太陽で加速して遠くに飛ばし、サンプルリターン等回収する場合は月で減速して大気でキャプチャーする
太陽駆動の月スイングバイ シーケンスの能力と小惑星探査への応用
2023年 2月 21日
概要
深宇宙ミッションの設計では、まず太陽と月の重力を考慮して利用することができます。
それらの重力は、宇宙船の打ち上げと宇宙船の回収だけでなく、エネルギー変化を提供することができます
小惑星。 小惑星回収ミッションに関しては、小惑星災害の軽減と容易な運用につながる可能性があります。
小惑星の探査と開発。 この論文では、太陽駆動の月のアプリケーションについて説明します。
小惑星ミッションのスイングバイ シーケンス。 この技術の能力を特徴づけることは興味深いだけではありません
動的な洞察の観点からだけでなく、軌道設計にとって自明ではありません。 この論文は容量を解明する
「Swingby-Jacobi」グラフを使用した、太陽による月のスイングバイ シーケンスの図。 容量は
現在カタログ化されている約 660 の小惑星を囲むヤコビ積分の範囲で表されます。 容易にする
軌道設計、多回転ケースを含む太陽摂動の月から月への移動のデータベースは、
生成され、使用されます。 その後、宇宙船の打ち上げと小惑星の捕獲のための大規模な軌道オプションが可能になります
調査し、最適化しました。 最後に、多数の小惑星フライバイ、ランデブー、サンプルリターン、および回収ミッション
提案された技術によって可能になるオプションが得られます。
キーワード
小惑星採掘 · 惑星防衛 · 重力アシスト · 小惑星フライバイ · サンプルリターン · 月から月へ転送 · 軌道設計 · 到達可能なセット
1 はじめに
宇宙ミッションと軌道設計では、重力アシストと低エネルギー転送を利用します。
天体の重力は、燃費を向上させるだけでなく、燃料消費を削減するためにしばしば考慮されます。
ペイロードの質量。 地球から出発するすべてのミッションで、月は最も近い天体です
重力アシストを提供できます。 実際、太陽-地球-月系の宇宙船は、太陽、地球、月からの共同重力効果。 などのミッションの軌道設計
HITEN、ARTEMIS-THEMIS、NOZOMI、DESTINY、EQUULEUS、Lunar Flashlight は、太陽潮汐によって駆動される月スイングバイを採用しています [1–7]。 共同重力効果は、宇宙船の打ち上げを支援し、
戻ってきた宇宙船の捕獲と、訪問した天体のサンプル。 しかし、関節重力
効果は、ミッション分析と軌道設計のために十分に特徴付けられていません。 本稿では、
太陽駆動の月スイングバイシーケンスの容量と小惑星回収への応用。
小惑星は、水とレアメタルを含んでいるかもしれない有望な大当たりと考えられています。 リソース
宇宙飛行士の生命を維持し、宇宙船に燃料を供給し、宇宙基地に電力を供給するために使用できます。 の開発
地球は、小惑星の採掘からも利益を得ることができます。 さらに、小惑星は非常に科学的に興味深いものです。
初期の太陽系の原始的な遺物を保存します。 DAWN、NEAR、はやぶさ 1 および 2 などのミッション、および
Osiris-REx は重要な情報と、より良い理解につながるサンプルさえも返しました。
小惑星と太陽系。 LUCY、PSYCHE、MMXなどのミッションが増えていきます。
小惑星や小惑星のような小さな天体を訪れています。 一方、地球近傍小惑星 (NEA) は脅威です。
地球への影響の絶え間ない可能性のために地球に。 チェリャビンスク流星は警報です。 「見る時」です。
アップ」し、潜在的な小惑星の攻撃に対処します。 NASA と ESA は、DART と HERA のミッションに取り組んでいます。
小惑星偏向技術を実証する[8、9]。 この文脈では、小惑星回収の概念も
提案されました。 小惑星回収とは、小惑星またはその一部を地球の近くに持ち込むことです。 それは
脅威を軽減するだけでなく、小惑星への簡単かつ継続的な訪問を可能にします。 さらにその技術は
小惑星の回収がより現実的になります。 たとえば、小さな NEA 全体を取得すると、およそ
2025 年までには、直径 7 m、重さ 50 万 kg のオーダーが可能になると考えられています [10]。
いくつかの研究は、推進技術と推進技術の観点から小惑星の回収を調査しました。
軌道設計。 この論文では、軌道設計の観点から問題を議論します。 このフレームでは、
リャドら。 (2014) [11] および Sanchez と Garcia Yárnoz (2016) [12] は、Sun-Earth libration-point を使用することを提案しました
小惑星捕獲のダイナミクス。 この方法は主に太陽の重力による自然な捕獲に依存しているため
と地球では、ターゲットを取得するのにかなりの時間または Δv がかかります。 さらに、ライブラリーポイント軌道は
不安定。 一定のステーションキーピング操作が必要ですが、これは長期的には実現不可能です。 それなし
捕獲された小惑星は、地球にとって深刻な危険になる可能性があります。 月スイングバイ缶
軌道エネルギーをより効果的に変化させます。 ランダウ等。 (2013) [13] および Gong and Li (2015) [14] が提案
月面スイングバイを使用。 この方法を使用すると、月に関する v∞ は不変であると見なされ、
その結果、月の軌道をはるかに超えた遠地点を持つ軌道は、常に月太陽の影響を受けます。
不安定で地球に脅威を与える摂動。 安定的に捕獲するためには、地球に対する固有エネルギーだけでなく、月に対する v∞ も最小化する必要があります。 Urrutxua等。
(2015) [15] は、太陽と地球の丘の問題に月の重力を含め、広範なシミュレーションを実行しました
数十から数百 m/s の Δv だけ延長された一時的なキャプチャ軌跡を明らかにします。 それにしてもコンクリート
太陽、地球、および月は、まだ不足しています。
この論文で調査された太陽駆動の月スイングバイ シーケンスは、両方に関して v∞ を変更できます。
地球と月、したがって、宇宙船を打ち上げて小惑星を高いところに捕獲するために使用することができます
地球に対して安定している月軌道または地球-月近直線ハロー軌道(NRHO)。 この論文では、
回収ミッションは 3 つのフェーズで検討されます。 地球の近くでは、脱出フェーズのために、
太陽駆動の月スイングバイ シーケンスは、地球に対する宇宙船の v∞ を増加させるためにも利用されます。
小惑星の特定の方向をターゲットとして。 キャプチャ フェーズでは、太陽主導の月スイングバイ シーケンス
月に対する小惑星の v∞ を許容可能な低いレベルに下げるために使用されます。
月に安定して閉じ込められた軌道への安価な挿入。 太陽中心移動段階では、宇宙船
は標的の小惑星に送られ、小惑星は許容される Δv で地球に送り返されます。 周りにある
現在カタログ化されている 15000 NEA。 可能な太陽中心移動と重力支援の検索と最適化
軌道は、更新された小惑星データベースが与えられるたびに、計算コストと時間がかかります。
多くの場合、キャパシティを特徴付けることが望まれます (つまり、到達可能なセット、達成可能なセット、または魅力的なセットと呼ばれます)。
初期推測を取得する目的で、特定の軌道設計方法の、枝刈り
検索空間など (例えば、参考文献 [16–20])。 関心のある問題については、Sun 駆動の容量を特徴付けます。
太陽中心のオブジェクトに到達してキャプチャするための月スイングバイ シーケンスは、興味深い点だけではありません。
動的な洞察だけでなく、ミッション計画にとって重要です。
グラフィカルな方法は、軌道の設計と分析に役立つ場合があります。 ストレンジとロングスキー
(2002) [21] は、重力アシストを分析および決定するための v∞ 等高線を持つティッセランド グラフを提案しました。
シーケンス。 これは、パッチを適用した 2 体近似に基づいています。 ポアンカレマップは、
三体問題。 Campagnola と Russell (2010) [22] は、Tisserand-Poincaré グラフをさらに発展させました。
スウィングバイ中の三体摂動を考慮した Tisserand (または Jacobi) 等高線を使用します。 ロス
and Scheeres (2007) [23] は、低エネルギーの捕獲と脱出を分析するために、近点-ポアンカレ マップを提案しました。
これらのグラフは、星と惑星と惑星と月のシステムに適用できます。 星・惑星・月系の場合
この作業に関係するのは、Chen らによって開発された Swingby-Jacobi グラフです。 (2016) [5] および陳 (2017) [24]
適用されます。 太陽地球系のヤコビ積分に加えて、月スイングバイの効果は
も描かれています。 Martens と Bucci (2022) [25] によって最近開発された double Tisserand グラフは注目に値します。
また、星-惑星-月系にも適用できます。 二重ティッセランドグラフは分析に適しています
Swingby-Jacobi グラフは、太陽中心への移動の分析に適しています。
領域。 Swingby-Jacobi グラフは、太陽駆動型のアクセシビリティを解明するために、この論文で採用されています。
太陽中心領域への月スイングバイシーケンス。
本稿の構成は以下のとおりである。 秒。 2 は、軌道設計に使用される動的モデルを示し、
太陽摂動月間移動 (SPMT) と月スイングバイのシーケンスのメカニズム
ミッションデザインの強化。 Sun-perturbed の効果を視覚化するために、Swingby-Jacobi グラフも導入されています。
乗り換えと月スイングバイ。 秒。 3 助けを借りて、太陽が駆動する月のスイングバイ シーケンスの容量を解明する
Swingby-Jacobi グラフの ヤコビ積分とアクセシブルのアクセシブルな範囲によって特徴付けられます
地球に対する v∞ の大きさと偏角のドメイン。 これらの範囲は効果的に除外します
最適化されたものの中で、間違いなくアクセスできない小惑星とアクセスできない太陽中心移動オプション
その計算ルーチンは Sec. に示されています。 4.1. SPMT セグメントと月面へのパッチ適用を容易にするため
脱出または捕獲条件を満たすためのスイングバイ、SPMT ソリューションのデータベースが確立されます。 の
データベースを計算する努力は、セクションに示されています。 4.2.1. この技術の特徴的な容量で
および軌道設計ツール、可能な小惑星フライバイ、ランデブー、サンプルリターン、および回収のリスト
次の 20 年間のミッションが取得され、セクションで提示されます。 5. デメリットとメリット
月から月への転送タイプ、すなわち、短い転送、太陽摂動転送、および 3 次元転送
転送、セクションで説明されています。 6. 結論は最後のセクションで与えられます。
7 結論
この論文では、太陽駆動の月スイングバイ シーケンスの容量とアプリケーションについて説明します。 いろいろな
Moon-to-Moon トランスファーのタイプ、すなわち、ショート トランスファー、Sun-perturbed トランスファー、multi-rev トランスファー、および
三次元転写について議論されました。 「Swingby-Jacobi」グラフによる分析は、
(1) 太陽駆動の月スイングバイ シーケンスは、-3.0009 から -2.9946 までのヤコビ積分範囲にアクセスできます。 これ
範囲には、現在カタログ化されている 657 の潜在的な小惑星が含まれており、ターゲット検索の労力を軽減できます
軌道の最適化。
(2) 脱出用の C3 は 4.8 km^2/s^2 に増やすことができます
逆に、この C3 レベルのオブジェクトは可能性があります (場合によっては月の周りを安定して境界付けられた軌道に取り込まれます(これには追加の
20 ~ 350 m/s の挿入 Δv)。 この手法は、少なくとも 1.46 km/s の v∞E に到達または吸収できます (つまり、2.13 km^2/s2 の C3) あらゆる方向に。
以前の地球と潜在的な候補との間の太陽中心移動軌道が最適化されました。
そして、太陽摂動のデータベースのおかげで、月のスイングバイの大規模なシーケンスが調査されました
月から月への転送。 結果は、
(3) 宇宙船が 2043 年までに ∆v コスト < 1 km/s で最初の小惑星と簡単にランデブーできる小惑星は 47 個あります。
月面遭遇。 ランデブー Δv がなくても、探査機は 1991 VG、2000 SG344、2014 YD、2016 TB18、2017 BN93 などの小惑星を 1 週間以上飛行して観測することができます。
低コストのミッションにとっては依然として重要です。
(4) 2043 年までに 21 個の小惑星サンプルを、地球再遭遇の Δv コスト < 500 m/s で取得できます。 特に、
最先端の発射および推進システムの能力を考慮して、1991年のVG全体を取得します
4.6 × 10^4 kN · s の全衝撃を必要とする 2038 年の次元 10 m の小惑星は実現可能であると考えられます。
付録 (地動説と月スイングバイ シーケンスのパッチ適用)
捕獲ケースを考えると、入射条件 v∞E と月の位置ベクトル rM を遭遇条件とすると、
地球に関する双曲軌道の軌道要素は、次のルーチンで計算できます。
この付録に示されています。 出会いの状況は2つあります。 ひとつの出会いが生まれる
インバウンド レグで、別の種類のエンカウンターがアウトバウンド レグで発生します (図 13 を参照)。 のために
inbound-capture の場合、遭遇時の真の異常 f とターン角 ζ の関係 (すなわち、
v∞E と rM の間の角度 β は、
cos f = cos(β − ζ) (13)
これは、次のように書き換えることができます。
cos f = sin β sin ζ + cos β cos ζ (14)
ζ は、地球に対する軌道の離心率 ep に関連しています。 したがって、
cos f = √e^2p − 1 / ep sinβ + 1/ep cosβ (15)
遭遇時、地球に対する長半径aの双曲線軌道の半径は同じです。
月の軌道の半径として、次のように表されます。
RM = ap(1 − e^2p) / 1 + ep cos f (16)
ここで、長半径 ap は v∞E に関連しています。
ap = −GE/v^2∞E (17)
ここで、GE は地球の重力パラメータです。 最後の 2 つの方程式を積分すると、二次方程式が得られます。

図 1 パッチを適用した Sun-Earth CR3BP と月スイングバイ モデルの概略図。
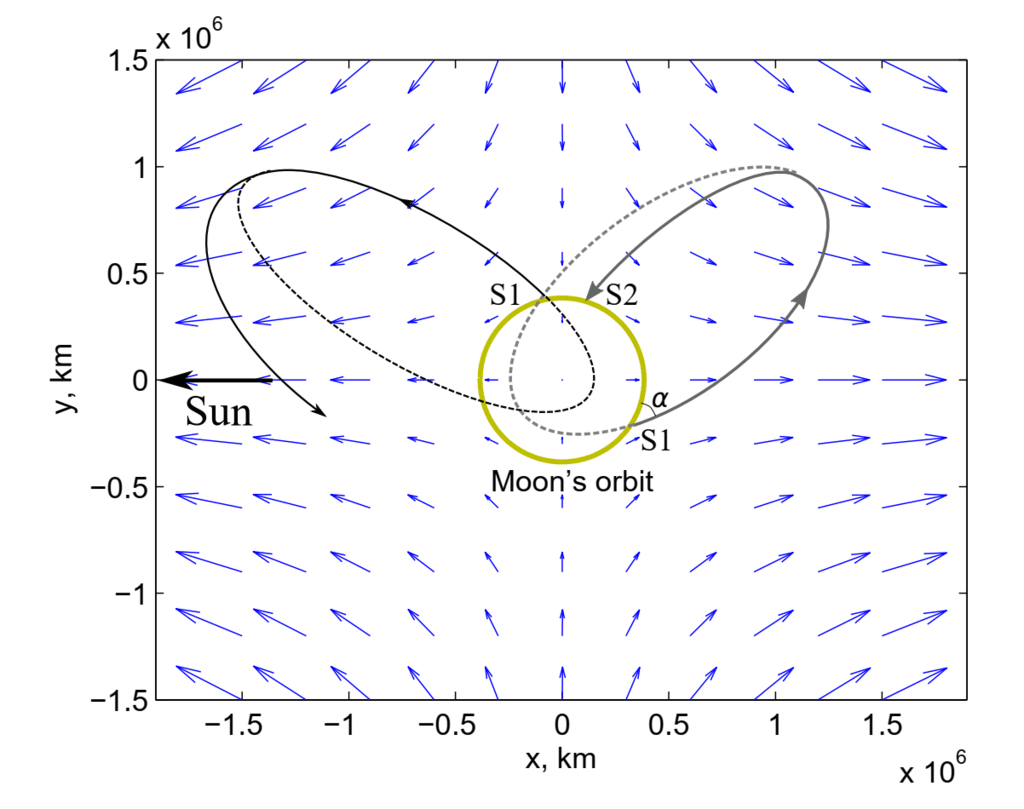
図 2 地球と月に関する軌道状態に対する太陽重力の影響 (図は参考文献 [5, 24])

図 3 スウィングバイ-ヤコビ グラフ
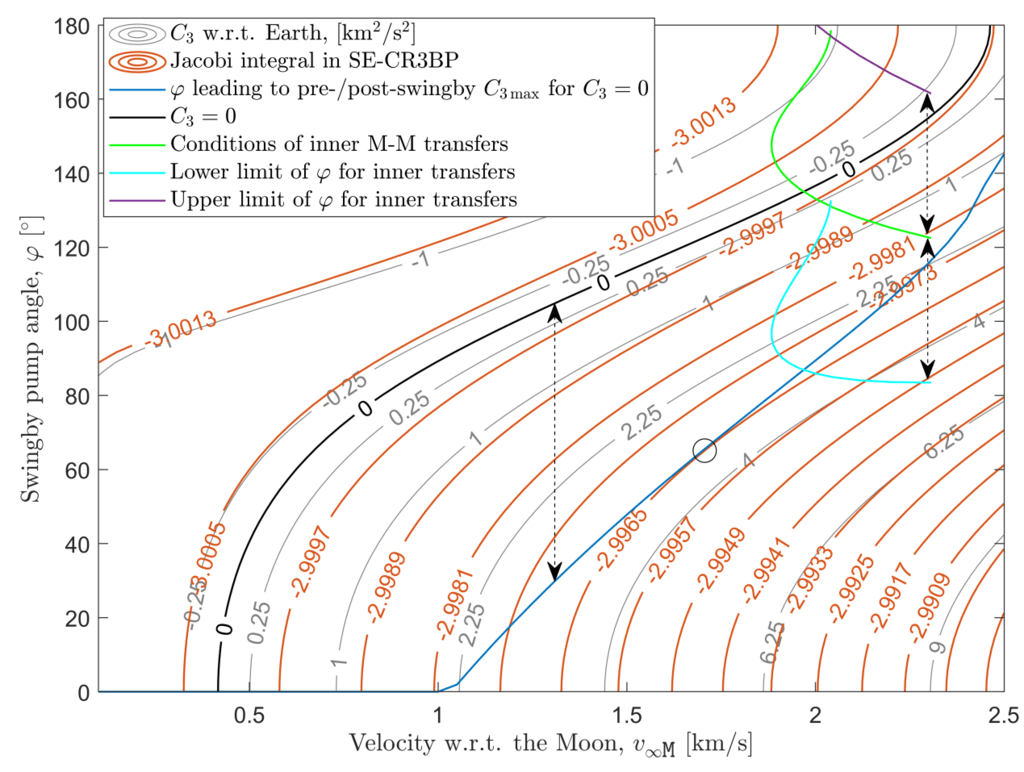
図 4 太陽が駆動する月スイングバイ シーケンスのキャパシティを、到達可能なヤコビ範囲の観点から明らかにする。

図 5 特定の速度と v∞M での月面遭遇状況。
太陽駆動の月スイングバイ シーケンスの能力と小惑星探査への応用
2023年 2月 21日
概要
深宇宙ミッションの設計では、まず太陽と月の重力を考慮して利用することができます。
それらの重力は、宇宙船の打ち上げと宇宙船の回収だけでなく、エネルギー変化を提供することができます
小惑星。 小惑星回収ミッションに関しては、小惑星災害の軽減と容易な運用につながる可能性があります。
小惑星の探査と開発。 この論文では、太陽駆動の月のアプリケーションについて説明します。
小惑星ミッションのスイングバイ シーケンス。 この技術の能力を特徴づけることは興味深いだけではありません
動的な洞察の観点からだけでなく、軌道設計にとって自明ではありません。 この論文は容量を解明する
「Swingby-Jacobi」グラフを使用した、太陽による月のスイングバイ シーケンスの図。 容量は
現在カタログ化されている約 660 の小惑星を囲むヤコビ積分の範囲で表されます。 容易にする
軌道設計、多回転ケースを含む太陽摂動の月から月への移動のデータベースは、
生成され、使用されます。 その後、宇宙船の打ち上げと小惑星の捕獲のための大規模な軌道オプションが可能になります
調査し、最適化しました。 最後に、多数の小惑星フライバイ、ランデブー、サンプルリターン、および回収ミッション
提案された技術によって可能になるオプションが得られます。
キーワード
小惑星採掘 · 惑星防衛 · 重力アシスト · 小惑星フライバイ · サンプルリターン · 月から月へ転送 · 軌道設計 · 到達可能なセット
1 はじめに
宇宙ミッションと軌道設計では、重力アシストと低エネルギー転送を利用します。
天体の重力は、燃費を向上させるだけでなく、燃料消費を削減するためにしばしば考慮されます。
ペイロードの質量。 地球から出発するすべてのミッションで、月は最も近い天体です
重力アシストを提供できます。 実際、太陽-地球-月系の宇宙船は、太陽、地球、月からの共同重力効果。 などのミッションの軌道設計
HITEN、ARTEMIS-THEMIS、NOZOMI、DESTINY、EQUULEUS、Lunar Flashlight は、太陽潮汐によって駆動される月スイングバイを採用しています [1–7]。 共同重力効果は、宇宙船の打ち上げを支援し、
戻ってきた宇宙船の捕獲と、訪問した天体のサンプル。 しかし、関節重力
効果は、ミッション分析と軌道設計のために十分に特徴付けられていません。 本稿では、
太陽駆動の月スイングバイシーケンスの容量と小惑星回収への応用。
小惑星は、水とレアメタルを含んでいるかもしれない有望な大当たりと考えられています。 リソース
宇宙飛行士の生命を維持し、宇宙船に燃料を供給し、宇宙基地に電力を供給するために使用できます。 の開発
地球は、小惑星の採掘からも利益を得ることができます。 さらに、小惑星は非常に科学的に興味深いものです。
初期の太陽系の原始的な遺物を保存します。 DAWN、NEAR、はやぶさ 1 および 2 などのミッション、および
Osiris-REx は重要な情報と、より良い理解につながるサンプルさえも返しました。
小惑星と太陽系。 LUCY、PSYCHE、MMXなどのミッションが増えていきます。
小惑星や小惑星のような小さな天体を訪れています。 一方、地球近傍小惑星 (NEA) は脅威です。
地球への影響の絶え間ない可能性のために地球に。 チェリャビンスク流星は警報です。 「見る時」です。
アップ」し、潜在的な小惑星の攻撃に対処します。 NASA と ESA は、DART と HERA のミッションに取り組んでいます。
小惑星偏向技術を実証する[8、9]。 この文脈では、小惑星回収の概念も
提案されました。 小惑星回収とは、小惑星またはその一部を地球の近くに持ち込むことです。 それは
脅威を軽減するだけでなく、小惑星への簡単かつ継続的な訪問を可能にします。 さらにその技術は
小惑星の回収がより現実的になります。 たとえば、小さな NEA 全体を取得すると、およそ
2025 年までには、直径 7 m、重さ 50 万 kg のオーダーが可能になると考えられています [10]。
いくつかの研究は、推進技術と推進技術の観点から小惑星の回収を調査しました。
軌道設計。 この論文では、軌道設計の観点から問題を議論します。 このフレームでは、
リャドら。 (2014) [11] および Sanchez と Garcia Yárnoz (2016) [12] は、Sun-Earth libration-point を使用することを提案しました
小惑星捕獲のダイナミクス。 この方法は主に太陽の重力による自然な捕獲に依存しているため
と地球では、ターゲットを取得するのにかなりの時間または Δv がかかります。 さらに、ライブラリーポイント軌道は
不安定。 一定のステーションキーピング操作が必要ですが、これは長期的には実現不可能です。 それなし
捕獲された小惑星は、地球にとって深刻な危険になる可能性があります。 月スイングバイ缶
軌道エネルギーをより効果的に変化させます。 ランダウ等。 (2013) [13] および Gong and Li (2015) [14] が提案
月面スイングバイを使用。 この方法を使用すると、月に関する v∞ は不変であると見なされ、
その結果、月の軌道をはるかに超えた遠地点を持つ軌道は、常に月太陽の影響を受けます。
不安定で地球に脅威を与える摂動。 安定的に捕獲するためには、地球に対する固有エネルギーだけでなく、月に対する v∞ も最小化する必要があります。 Urrutxua等。
(2015) [15] は、太陽と地球の丘の問題に月の重力を含め、広範なシミュレーションを実行しました
数十から数百 m/s の Δv だけ延長された一時的なキャプチャ軌跡を明らかにします。 それにしてもコンクリート
太陽、地球、および月は、まだ不足しています。
この論文で調査された太陽駆動の月スイングバイ シーケンスは、両方に関して v∞ を変更できます。
地球と月、したがって、宇宙船を打ち上げて小惑星を高いところに捕獲するために使用することができます
地球に対して安定している月軌道または地球-月近直線ハロー軌道(NRHO)。 この論文では、
回収ミッションは 3 つのフェーズで検討されます。 地球の近くでは、脱出フェーズのために、
太陽駆動の月スイングバイ シーケンスは、地球に対する宇宙船の v∞ を増加させるためにも利用されます。
小惑星の特定の方向をターゲットとして。 キャプチャ フェーズでは、太陽主導の月スイングバイ シーケンス
月に対する小惑星の v∞ を許容可能な低いレベルに下げるために使用されます。
月に安定して閉じ込められた軌道への安価な挿入。 太陽中心移動段階では、宇宙船
は標的の小惑星に送られ、小惑星は許容される Δv で地球に送り返されます。 周りにある
現在カタログ化されている 15000 NEA。 可能な太陽中心移動と重力支援の検索と最適化
軌道は、更新された小惑星データベースが与えられるたびに、計算コストと時間がかかります。
多くの場合、キャパシティを特徴付けることが望まれます (つまり、到達可能なセット、達成可能なセット、または魅力的なセットと呼ばれます)。
初期推測を取得する目的で、特定の軌道設計方法の、枝刈り
検索空間など (例えば、参考文献 [16–20])。 関心のある問題については、Sun 駆動の容量を特徴付けます。
太陽中心のオブジェクトに到達してキャプチャするための月スイングバイ シーケンスは、興味深い点だけではありません。
動的な洞察だけでなく、ミッション計画にとって重要です。
グラフィカルな方法は、軌道の設計と分析に役立つ場合があります。 ストレンジとロングスキー
(2002) [21] は、重力アシストを分析および決定するための v∞ 等高線を持つティッセランド グラフを提案しました。
シーケンス。 これは、パッチを適用した 2 体近似に基づいています。 ポアンカレマップは、
三体問題。 Campagnola と Russell (2010) [22] は、Tisserand-Poincaré グラフをさらに発展させました。
スウィングバイ中の三体摂動を考慮した Tisserand (または Jacobi) 等高線を使用します。 ロス
and Scheeres (2007) [23] は、低エネルギーの捕獲と脱出を分析するために、近点-ポアンカレ マップを提案しました。
これらのグラフは、星と惑星と惑星と月のシステムに適用できます。 星・惑星・月系の場合
この作業に関係するのは、Chen らによって開発された Swingby-Jacobi グラフです。 (2016) [5] および陳 (2017) [24]
適用されます。 太陽地球系のヤコビ積分に加えて、月スイングバイの効果は
も描かれています。 Martens と Bucci (2022) [25] によって最近開発された double Tisserand グラフは注目に値します。
また、星-惑星-月系にも適用できます。 二重ティッセランドグラフは分析に適しています
Swingby-Jacobi グラフは、太陽中心への移動の分析に適しています。
領域。 Swingby-Jacobi グラフは、太陽駆動型のアクセシビリティを解明するために、この論文で採用されています。
太陽中心領域への月スイングバイシーケンス。
本稿の構成は以下のとおりである。 秒。 2 は、軌道設計に使用される動的モデルを示し、
太陽摂動月間移動 (SPMT) と月スイングバイのシーケンスのメカニズム
ミッションデザインの強化。 Sun-perturbed の効果を視覚化するために、Swingby-Jacobi グラフも導入されています。
乗り換えと月スイングバイ。 秒。 3 助けを借りて、太陽が駆動する月のスイングバイ シーケンスの容量を解明する
Swingby-Jacobi グラフの ヤコビ積分とアクセシブルのアクセシブルな範囲によって特徴付けられます
地球に対する v∞ の大きさと偏角のドメイン。 これらの範囲は効果的に除外します
最適化されたものの中で、間違いなくアクセスできない小惑星とアクセスできない太陽中心移動オプション
その計算ルーチンは Sec. に示されています。 4.1. SPMT セグメントと月面へのパッチ適用を容易にするため
脱出または捕獲条件を満たすためのスイングバイ、SPMT ソリューションのデータベースが確立されます。 の
データベースを計算する努力は、セクションに示されています。 4.2.1. この技術の特徴的な容量で
および軌道設計ツール、可能な小惑星フライバイ、ランデブー、サンプルリターン、および回収のリスト
次の 20 年間のミッションが取得され、セクションで提示されます。 5. デメリットとメリット
月から月への転送タイプ、すなわち、短い転送、太陽摂動転送、および 3 次元転送
転送、セクションで説明されています。 6. 結論は最後のセクションで与えられます。
7 結論
この論文では、太陽駆動の月スイングバイ シーケンスの容量とアプリケーションについて説明します。 いろいろな
Moon-to-Moon トランスファーのタイプ、すなわち、ショート トランスファー、Sun-perturbed トランスファー、multi-rev トランスファー、および
三次元転写について議論されました。 「Swingby-Jacobi」グラフによる分析は、
(1) 太陽駆動の月スイングバイ シーケンスは、-3.0009 から -2.9946 までのヤコビ積分範囲にアクセスできます。 これ
範囲には、現在カタログ化されている 657 の潜在的な小惑星が含まれており、ターゲット検索の労力を軽減できます
軌道の最適化。
(2) 脱出用の C3 は 4.8 km^2/s^2 に増やすことができます
逆に、この C3 レベルのオブジェクトは可能性があります (場合によっては月の周りを安定して境界付けられた軌道に取り込まれます(これには追加の
20 ~ 350 m/s の挿入 Δv)。 この手法は、少なくとも 1.46 km/s の v∞E に到達または吸収できます (つまり、2.13 km^2/s2 の C3) あらゆる方向に。
以前の地球と潜在的な候補との間の太陽中心移動軌道が最適化されました。
そして、太陽摂動のデータベースのおかげで、月のスイングバイの大規模なシーケンスが調査されました
月から月への転送。 結果は、
(3) 宇宙船が 2043 年までに ∆v コスト < 1 km/s で最初の小惑星と簡単にランデブーできる小惑星は 47 個あります。
月面遭遇。 ランデブー Δv がなくても、探査機は 1991 VG、2000 SG344、2014 YD、2016 TB18、2017 BN93 などの小惑星を 1 週間以上飛行して観測することができます。
低コストのミッションにとっては依然として重要です。
(4) 2043 年までに 21 個の小惑星サンプルを、地球再遭遇の Δv コスト < 500 m/s で取得できます。 特に、
最先端の発射および推進システムの能力を考慮して、1991年のVG全体を取得します
4.6 × 10^4 kN · s の全衝撃を必要とする 2038 年の次元 10 m の小惑星は実現可能であると考えられます。
付録 (地動説と月スイングバイ シーケンスのパッチ適用)
捕獲ケースを考えると、入射条件 v∞E と月の位置ベクトル rM を遭遇条件とすると、
地球に関する双曲軌道の軌道要素は、次のルーチンで計算できます。
この付録に示されています。 出会いの状況は2つあります。 ひとつの出会いが生まれる
インバウンド レグで、別の種類のエンカウンターがアウトバウンド レグで発生します (図 13 を参照)。 のために
inbound-capture の場合、遭遇時の真の異常 f とターン角 ζ の関係 (すなわち、
v∞E と rM の間の角度 β は、
cos f = cos(β − ζ) (13)
これは、次のように書き換えることができます。
cos f = sin β sin ζ + cos β cos ζ (14)
ζ は、地球に対する軌道の離心率 ep に関連しています。 したがって、
cos f = √e^2p − 1 / ep sinβ + 1/ep cosβ (15)
遭遇時、地球に対する長半径aの双曲線軌道の半径は同じです。
月の軌道の半径として、次のように表されます。
RM = ap(1 − e^2p) / 1 + ep cos f (16)
ここで、長半径 ap は v∞E に関連しています。
ap = −GE/v^2∞E (17)
ここで、GE は地球の重力パラメータです。 最後の 2 つの方程式を積分すると、二次方程式が得られます。

図 1 パッチを適用した Sun-Earth CR3BP と月スイングバイ モデルの概略図。

図 2 地球と月に関する軌道状態に対する太陽重力の影響 (図は参考文献 [5, 24])

図 3 スウィングバイ-ヤコビ グラフ

図 4 太陽が駆動する月スイングバイ シーケンスのキャパシティを、到達可能なヤコビ範囲の観点から明らかにする。

図 5 特定の速度と v∞M での月面遭遇状況。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます