
木星の極にある深く、密集した、長寿命のサイクロン
2021年3月16日に提出
木星へのジュノーミッションは、惑星の2つの極で密集したサイクロンを発見しました。これらのサイクロンが非常に限られた空間で共存し、外側の縁がほとんど互いに接触しているが、融合していないという観察は、大きなパズルを引き起こします。この研究では、対流が持続し、密集したサイクロンが、深く回転する対流層の極域(数千の惑星の自転周期)で非常に長い時間融合することなく形成され、生き残ることができることを示す数値計算を提示します。軸対称循環の慣性安定性基準の理想的な適用を通じて、極の近くの大きなコリオリパラメータがサイクロンを密に詰めることを可能にする上で重要な役割を果たすことがわかります。

図1.シミュレーションと観測の間のポリゴンパターンの比較。上部のパネルは、放射対流境界付近の瞬間的な温度場の水平方向のカットを示しています。(A)シミュレートされた
五角形のケース。大小の破線の円は70◦と80◦を示しています
それぞれ緯度。用語で
寸法単位の場合、この層の温度コントラストは約35Kです。 (B)シミュレートされた六角形の場合。
大小の破線の円は80◦と85◦を示しています
それぞれ緯度。温度コントラスト
この層では約22Kです。渦の外縁の渦巻きが目立つように現れます。下部パネル
(C)は、木星の南極でJIRAMによって観測された画像を示しています(Adriani et al.2018)。図1Cの礼儀
アレッサンドロムラとアルベルトアドリアーニの。図1Cは、参考文献Adriani etal。の許可を得て転載しています。
(2018)、Springer Nature:Nature、著作権(2018)。 (A)と(B)は北から見たものであることに注意してください(サイクロン
動きは反時計回りです)、(C)は南から見ています(サイクロンの動きは時計回りです)。

図2.ボックスの中央(z = 0.5)での瞬間的な流れの特性。 (A)は水平を示しています
ケースAの垂直渦度フィールドのカット。明るい(暗い)色は、より高い(より低い)渦度を表します。 に
寸法形状、1距離単位は約3668kmです。 (B)は対応する水平速度を示しています
合理化。 (C)と(D)は(A)と(B)に似ていますが、ケースBの場合です。寸法形式では、1つの距離単位約1840kmです。

図3.サイクロンはCZの深さ全体に浸透し、程度は低いもののRZまで伸びています。 (A)と
(B)五角形と六角形の場合の相対的な温度変化の垂直カット(y = 8)を示します。
それぞれ。
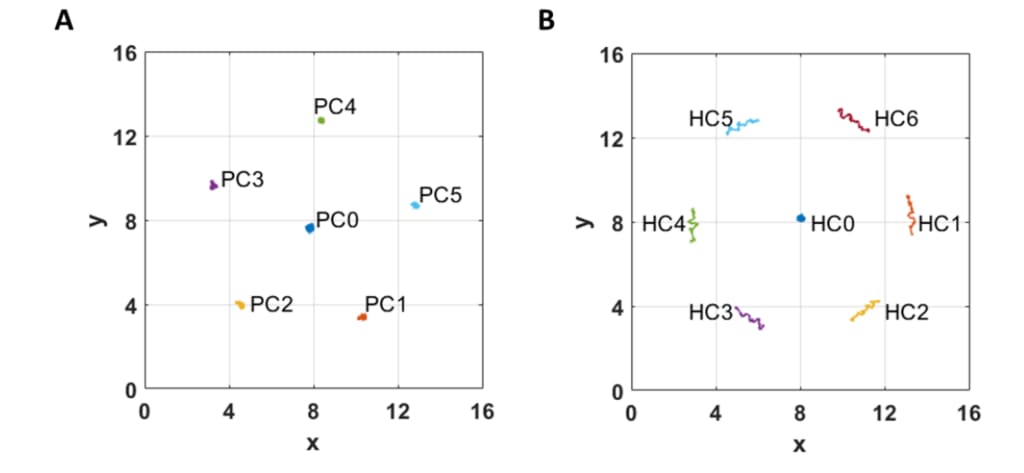
図4.ボルテックストラック。 (A)と(B)は、五角形と六角形の中心の位置を追跡します
それぞれ渦。 追跡は約96の惑星の自転周期の間続きました。

図5.中央の渦の動き。 PC0の場合、(A)は時間平均位置までの瞬間距離を示し、(B)は本文で定義されている位置角度を示します。 (C)および(D)は、HC0に対応する量を示しています。
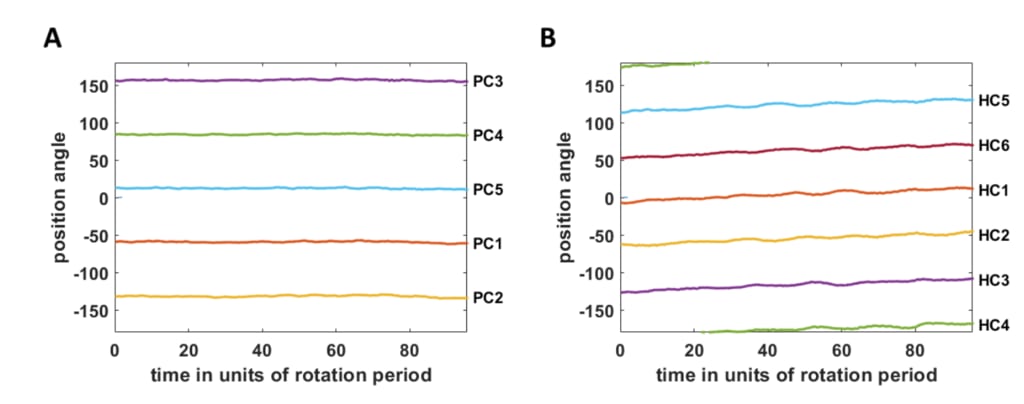
図6.周極渦の動き。 (A)と(B)は中心から外れた渦の位置角を示しています
それぞれ五角形と六角形の場合。 五角形のパターンは目立たないが
回転すると、六角形のパターンが中央のサイクロンの周りを惑星ごとに約0.17◦の割合でドリフトします。
自転周期。

図7.渦の周りの接線速度分布。 (A)と(B)は、それぞれPC0とHC0の中心の周りの瞬間接線速度(z = 0.5)のコンタープロットです。 黒の破線
円は距離r = 1.5を示します。

図8.接線速度の合計パワーに対する軸対称モードのパワーm = 0。
値は、シミュレーションの終わりに向かって10の惑星の自転周期にわたって平均されます。 (A)プロット
PC0(青い曲線)とPC2(オレンジ色の曲線)の比率。 (B)HC0(青い曲線)とHC2の比率をプロットします
(オレンジ色の曲線)。
2021年3月16日に提出
木星へのジュノーミッションは、惑星の2つの極で密集したサイクロンを発見しました。これらのサイクロンが非常に限られた空間で共存し、外側の縁がほとんど互いに接触しているが、融合していないという観察は、大きなパズルを引き起こします。この研究では、対流が持続し、密集したサイクロンが、深く回転する対流層の極域(数千の惑星の自転周期)で非常に長い時間融合することなく形成され、生き残ることができることを示す数値計算を提示します。軸対称循環の慣性安定性基準の理想的な適用を通じて、極の近くの大きなコリオリパラメータがサイクロンを密に詰めることを可能にする上で重要な役割を果たすことがわかります。

図1.シミュレーションと観測の間のポリゴンパターンの比較。上部のパネルは、放射対流境界付近の瞬間的な温度場の水平方向のカットを示しています。(A)シミュレートされた
五角形のケース。大小の破線の円は70◦と80◦を示しています
それぞれ緯度。用語で
寸法単位の場合、この層の温度コントラストは約35Kです。 (B)シミュレートされた六角形の場合。
大小の破線の円は80◦と85◦を示しています
それぞれ緯度。温度コントラスト
この層では約22Kです。渦の外縁の渦巻きが目立つように現れます。下部パネル
(C)は、木星の南極でJIRAMによって観測された画像を示しています(Adriani et al.2018)。図1Cの礼儀
アレッサンドロムラとアルベルトアドリアーニの。図1Cは、参考文献Adriani etal。の許可を得て転載しています。
(2018)、Springer Nature:Nature、著作権(2018)。 (A)と(B)は北から見たものであることに注意してください(サイクロン
動きは反時計回りです)、(C)は南から見ています(サイクロンの動きは時計回りです)。

図2.ボックスの中央(z = 0.5)での瞬間的な流れの特性。 (A)は水平を示しています
ケースAの垂直渦度フィールドのカット。明るい(暗い)色は、より高い(より低い)渦度を表します。 に
寸法形状、1距離単位は約3668kmです。 (B)は対応する水平速度を示しています
合理化。 (C)と(D)は(A)と(B)に似ていますが、ケースBの場合です。寸法形式では、1つの距離単位約1840kmです。

図3.サイクロンはCZの深さ全体に浸透し、程度は低いもののRZまで伸びています。 (A)と
(B)五角形と六角形の場合の相対的な温度変化の垂直カット(y = 8)を示します。
それぞれ。

図4.ボルテックストラック。 (A)と(B)は、五角形と六角形の中心の位置を追跡します
それぞれ渦。 追跡は約96の惑星の自転周期の間続きました。

図5.中央の渦の動き。 PC0の場合、(A)は時間平均位置までの瞬間距離を示し、(B)は本文で定義されている位置角度を示します。 (C)および(D)は、HC0に対応する量を示しています。

図6.周極渦の動き。 (A)と(B)は中心から外れた渦の位置角を示しています
それぞれ五角形と六角形の場合。 五角形のパターンは目立たないが
回転すると、六角形のパターンが中央のサイクロンの周りを惑星ごとに約0.17◦の割合でドリフトします。
自転周期。

図7.渦の周りの接線速度分布。 (A)と(B)は、それぞれPC0とHC0の中心の周りの瞬間接線速度(z = 0.5)のコンタープロットです。 黒の破線
円は距離r = 1.5を示します。

図8.接線速度の合計パワーに対する軸対称モードのパワーm = 0。
値は、シミュレーションの終わりに向かって10の惑星の自転周期にわたって平均されます。 (A)プロット
PC0(青い曲線)とPC2(オレンジ色の曲線)の比率。 (B)HC0(青い曲線)とHC2の比率をプロットします
(オレンジ色の曲線)。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます