2024/04/11 Prolog、光明
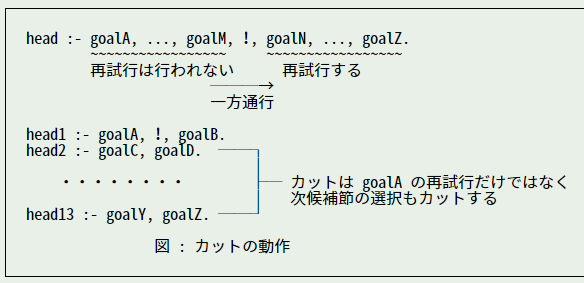
カットか・・うーん、なんか分かりにくい。嘘です、分かりません。再帰の時に再試行を行わないってこと?

ははぁ・・勝手にバックトラックされてしまう仕組みなのか。それでこれまでにも自明と思われてた条件が書かれていることがあったということか?

こうやって実装していくのか・・

お〜・・なんか馴染みのある記述が出来るようになってきてるじゃないか

とりあえず先に進むか・・と。おや?ああっ!!これか!
やっとこさ分かった・・今までどうもうまいこと書けなかった理由が!普通の再帰と末尾再帰の書き分けが出来て無かったんか!というかそういう種類があると分かって無かったんですけど。自然と末尾再帰の書き方をしてたんだけど、ちゃんと分かってないからFalseになってたんではないかと。

上が自作、下が解答。見比べると・・あ、X>1がX>0にしないといけなかったか。けど、他は合ってる。

次の演習もやってみる。こうかな?
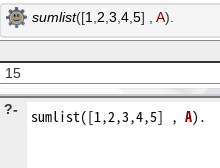
合ってる! なんだよそういう事か〜・・やる気がムンムン湧いてきたぜ!
2024/04/06
話題その1 気分転換にRustの本を読む

先日図書館で予約しておいた実践Rust入門が届いたので気分転換にパラパラを読み進める。ふ〜ん・・もっとC言語的な書き方をしないといけないのかと思ってたけどそうでも無いんだなぁ、とか

面白かったのは関数などの命名規則が言語の仕様として決まってる所とか?確かに命名は悩みますもんねぇ。
ま、とりあえず読書としてザーッと読むだけ読んでおこう。ひょっとすると無意識の領域で理解が進んで本番で理解が容易になるかも知れんし。
話題その2 Prolog

木構造の置き換え、第一引数がリストの場合もあるのか・・

ルール3って必要なのか?と思ったのでコメントアウトしてテスト
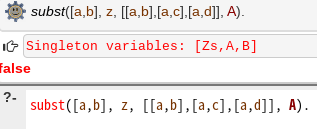
やっぱり必要なのか・・

うーん・・改めて分かったけど僕には論理力が足りない!ということは是非ともPrologをやった方が良いわけで、今後もネットリと頑張ります。
2024/04/05 Prolog、例によって続き

続いてリスト中にある任意の要素を数えるCount。上が自作で下が解答。
コレコレ!目的の変数Nを更新していくパターンの時に、またBody部のN1を更新するように書いてしまう。
あとルール2でXとYが同一でないという部分。一応テストしたけど書かなくても問題無いんだよなぁ。なんで書くんだろう?

続いて
「引数 X と等しいリスト Xs の要素を Y に置き換える substitute(X, Y, Xs, Zs)」
って問題。上の2つが自作で3つ目が解答。
1つ目はHead部で変数の組み換えをするパターンで、Prologの元からある機能で当てはまる値がProlog側で収集されるというのを目指したパターン。
2つ目はBody部でP1を新たに束縛して?って感じで出来ないかなぁ・・と試したパターン。出来ませんでした!
解答を見ると1つ目のパターンが近い。細いところに目を瞑れば書けてると言っても良いかな?

そう言えばここからは完全初見。木構造の操作は全く想像がつかない・・なので解答をコピーして日本語訳を書いていく。
うーん、なるほど・・ルール1で入れ子形式単一リストをCarとCdr部に分解してそれぞれ再帰、ルール2にて葉1枚につきNは1で返ってくるから、全部足し合わせるようになる・・と。こんなん絶対に書けない自信がある!しばらく木構造の理解に時間を使わないといけない予感するなぁ。

一応その次の演習も日本語訳してみる。一応自作を試みたが、すかさず無理だと悟る。上のは残骸。
ルール1は恐らく・・分解が進んで要素のみになった場合にXをYに置換するためのもの。
ルール2はリスト2つをそれぞれ左右の葉に分解して、左葉同士、右葉同士で再帰させる・・
ルール3はなんだ?出力用か?ちょっとこれは有る無しテストをしてみないと分からん。
というわけで、次回からはPrologで木構造の理解に挑戦することになりそう。これは長い道のりになるぜ(確信)。
2024/04/04 Prolog、続き

続きをやっていく。リスト1がリスト2のケツ部分と同一か?という述語。
うーん・・こういう感じかなぁ・・
リスト2の頭から消していって、ある時点でリスト1と同じであれば条件成立。ルール1で成立条件、ルール2でリストイート、と。

おおっ!やったぜ!

続いてFlatten。駄目、書けない。解答を拝見、あ〜これは分かりませんわ。XとXsに分けて、Xがリストじゃない場合とリストの場合をそれぞれ再帰してAppendすると。Appendでは空リストは省かれる、リストから出た場合を改めてリストに入れるようにすることで最終的に単一のリストに出来るのか

整数を取り出す。取り出すのがAtomじゃなくてIntegerだってだけの話だけど・・Flattenが分からなかったら分からないな。まあでもこれはまずは形で覚えるしか無いのではなかろうか

リスト中の任意のAtomが何番目かを示す述語。うーん、これは思いつかない。そもそも、述語の名前が同じで引数の数が違うって・・関数だと思って読むと混乱するなぁ。パターンマッチングってことで、引数が3つの時には3つの時の動きってことで分けられるのは面白いっすねぇ。
ルール1は終了条件で一致したらNはIと同じになる。でなければ、リストを更新しつつIを1ずつ増やす・・読んだら分かるんだけどねぇ。英作文と一緒でまずはリーディングが出来るようになったらライティングも出来るようになるのだろうか?
2024/04/02 Prolog、お気楽に戻ってみる

続きはPrefixからなので挑戦。一周目の事は完全に忘れてるので、こういう時には便利だな。さて、リスト1がリスト2の前方と一致しているか?という述語だから・・一度はルール1に再帰を仕込んで・・と思ったんだけど、例の工業大学生さんのルールを思い出す「望む結果が1つだったら空白の終了条件」だったよな・・と。今回は基本述語だけど、Xsを自由変数にした場合にはNextで複数の候補が出力されるはずだから、解が複数パターンになるはず?
ということでルール1での再帰をやめて「望む解の形」を考える。リスト1とリスト2の頭からある部分までのCar(X)が同じならばOKなんだから・・こうか?ルール2はただ再帰をするだけのため。さて・・・?

やったぜ!述語としてはちゃんと動いている。しかしTrueの場合にNextのボタンが・・?
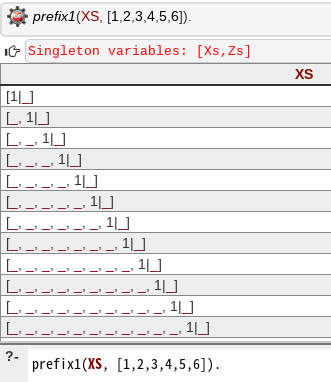
候補が現れるはずのXsを自由変数にした場合を試すと・・ぬわ〜なんだこれは!?

上が自作、下が解答。あ、最初の構想で良かったのか・・単純にリスト1が尽きたら終了、そりゃそうだ。こうやって見ると自明に思えるんだけどなぁ
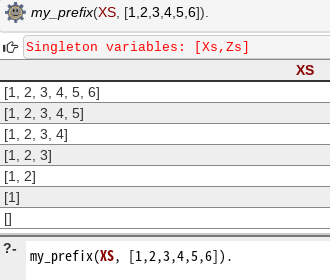
本来、Xsを自由変数にするとこういう感じの動きになるはずなんだけど。いやまあでも、数ミリくらいは進歩してる気がするし続きます
2024/04/01 Prolog、別のページでやり直してみる
ひょっとすると別の方の解説を読めば光明が見えるかも?と思ったので、こちらのページを拝見する。
ほほ〜・・なるほど。
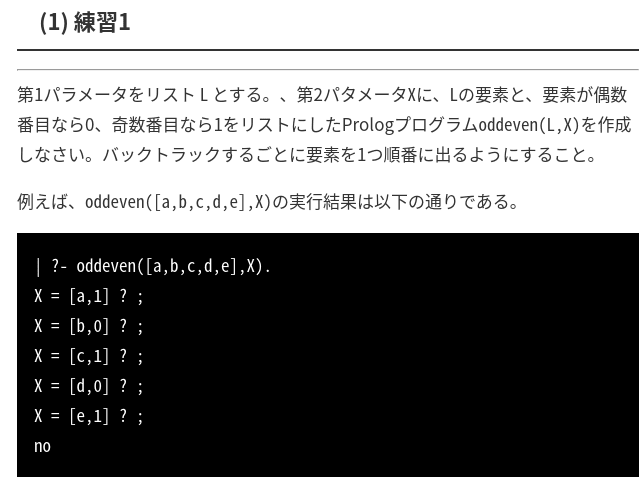
練習問題をやってみる。と言っても、ちゃんと問題を読んでなかったので間違ったことに取り組んだのですが。

うーん、こうか?
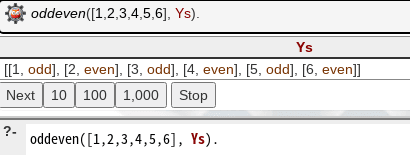
(出題者の意図を間違って理解しているが)自分で考えた通りには動いているぞ!と思ったら・・あれ?Nextがある?

ぬわ〜なんだこれは!?

解答を見る。まあ、もともと間違ったお題を解こうとしているので問題外なのだが・・。
思うに、ファクトとルールがまだ曖昧。望む結果はファクトとして出力されるはずだから・・初期値、停止条件、呼び方は違うが求めるのはファクトなのだ、ということなのか。

先程のNextが出てきた問題の解決になりそうなまとめがあったのでスクショ。
本来の出題意図では解が複数だったのでNextが出るのは良かったが・・僕の狙いとしては「解が1つのとき」のはずなのに、図らずも「解が複数のとき」の書き方になってしまっていたわけか・・?
解が複数のときは、それぞれの条件をファクトとして設定する、これは間違い無かろう(出来てなかったわけだが)。後はリストを進める再帰部分を書けばいいだけなのに、再帰部分を複数書いてしまったために2重ループみたいになったということなのか?

とりあえず次の例題も見てみる。重複要素を排除する述語。

ところが、こちらでは再帰部分が複数あるのにも関わらず解は1つなのだ。じゃあやっぱり僕の場合は解となる条件と再帰を行う部分が被ってしまってるということ・・だろうか
うーん、こんだけ手こずるやつも珍しいのでは無いだろうか?という気もするが、「工業大学生ももやまうさぎ」さんは「数学と情報が得意」らしい。僕は「数学も情報も苦手」なので、なかなか出来なくても何らおかしな事はない!ということで続けますw
2024/03/30 Prolog、別の方向から見る必要がありそう

Selectsが書けたのでイケるのでは!?と思って続きをやったけど、すぐさま思い知る。書けねぇ〜
Procuctはまだ解答を読めば「そうか・・そうかも」と分かるんだけど、冪集合のPowerは正解を読んでも分からない。

いや、結果から見たら分かるんですよ。XsのCar部分がX、それと同じ条件を満たすリストを考えたら1,2,3 1,2 1,3 1。なるほど。
で、ルール2でXsのCdrで再帰をする。と、それにルール1を当てはめて・・確かに!
あれ・・?昨日取り組んでる時にはこういう風に考えられなかったのだ。思うにルール1の部分を普通の再帰の手続き?みたいに値を取り出すアルゴリズムみたいなのを考えようとしてるのがおかしかった。Prologだと勝手に探して列挙してくれるんだから・・うーん、なんで昨日は分からなかったのかなぁ・・。あ、ルールごとに条件を満たせば枝分かれをすると考えたからでは?今のPrologの列挙を自分でやらないといけないと考えていたのは枝分かれを使って自分で取り出さないといけないと思ってたからじゃなかろうか

分からなさすぎてClaudeに聞いてみたりもした。これがまた余計に混乱の元になってしまった。前に聞いた時には複数のルールが満たされる条件だったらどちらにも適用されて枝分かれするとかって言ってたじゃない!しかしこの時には「上から優先して適用され枝分かれはしない」という。
ま、確かにPower_setの例で言うとその通りになってる、よな・・

困り果てた昨日の僕は「Prolog 難しい」でGoogle検索をかけたのだ。もしかして難しいと感じる人が書いた記事だったら助けになるかと思ったから。
そうしたところ
この方のブログがヒットして、なるほど京大理系卒のプログラマーでも「最難関」と言うんだから俺が難しいと困り果ててもしょうがない!と。ある意味安心したのですが、そのままこの方のブログを読みふけってしまうという事態に。
とりあえずこの方はその後生活が大変な事になってしまっててPrologの記事を1本書かれただけになってしまっているので参考として出されてた神戸大学のページに飛んで最初から読み始めてます。
が、検索・列挙はPrologがやってくれるんだから・・と考えたら光明が見えるかも知れん。予定を変えてお気楽の2周目を続けよう
2024/03/29 Prolog、諦めない
宿直での厨房作業追加に知り合いからの呼び出し、神戸に雑用発生・・と、ほぼ一週間ぶりにProlog学習に戻ってまいりました。
あ〜・・きっと何も出来なくなってるだろうなぁ・・と心配になりながら再開。まずは部分集合うんぬん!って言うSelect、Selects。

うーん、こういう感じかなぁ・・

ええっ!?なんと一発でヒント無しにて書くことが出来た。

書く時にテキストエディタに実際の値を書いてから取り組んだのが良かったのかも知れん

もしかして一週間のうちに脳内で学習が熟成されて書けるようになってるんじゃないか?と思ったのだが・・直積集合は全然駄目でした。というか補助述語を作らないといけないというのが、もう、駄目でした。

読み解きのためにテキストエディタに実際の値の流れを書く。条件が満たされていればルールは並行して適用されるというのを念頭に置いて読み解くと、一周目とは違う理解感が得られた気がする・・
とりあえず、要素が複数変化して組み合わせしないといけない場合は補助関数を使う・・ってのを仮説として覚えておこうか。
気になったのは通常の再帰述語と違って停止ルールが設定されてない点。Falseになった時点で終わるからOKな時と明確に停止条件を作らないといけない場合の違いは・・うーん・・
・ルールが複数ある
・1つのルールで出力が約束されている
・1つのルールは再帰専用で失敗=停止となる
という感じだろうか?
これはいずれ3周目をしないといけない予感。
2024/03/24 楽園失陥
週に2〜3日、実働2時間半で高速WIFI完備の宿直バイトにてプログラミング学習を楽しんでまいりましたが・・突然の悲報、追加の業務が言い渡される事に。
夜は20時までだった清掃業務の後、追加で2時間ラウンジにて待機しつつ入居者が徘徊していた場合には夜勤者に通報するという警戒任務が・・ま、これは良い。どうせテーブルに座ってノートパソコン触れるからな。
が、今まで8時半まで待機だったのに6時から厨房で朝食の準備と配膳の業務が追加されてしまったのだ!5時半には起きないといけないし、今までみたいに30分掃除をして帰宅する・・みたいな甘い労働ではないので(昨日初回の研修があったんだけどナカナカの作業)・・夜はとっとと寝ないとイカン!
うーん・・まあ、今までがあんまりにも美味しすぎたって話なんですけどね。普通のバイトになってしまったなぁ・・。あ、日給は2000円上がりますけど(労働時間が4時間半増えるのだが)。飲食のバイトなんて30年ぶりだけど、そこはプログラミング学習で鍛えた関数型プログラミング思考法で業務の最適化に挑戦してみたろうと思います。
問題は入居者の顔と名前が全く一致しない為に、ラウンジに入ってきたのを確認→配膳準備で詰まってしまう事。これをなんとかハイテクで効率化出来ないか・・中国の顔認証システムみたいなのでラウンジ入り口の通過時に厨房内にずんだもんボイスで通知・・みたいなのが出来たら楽なんだけどなぁ。
というわけでProlog学習ペースは(もともと遅いのに更に)落ちそうです・・
2024/03/22

続けてMemberを作ってみる。上が自作で下がお手本、うーん・・変数の並びが逆だけど同じことをやってるかな。テストもオッケイ

続いてSelectの実装。あるリストから任意の要素を指定すると、要素を除いたリストを返すというもの。
上が自作で下がお手本・・テストはオッケイだったんだけどお手本はスマートで自作は非Prolog脳って感じ?まあ、結果が一緒だったら良いかとも思うけど。

続いてリストAがリストBの部分集合かどうか?をチェックするSelects。実は自分で考えたと言うよりも周回プレイなので画像で覚えてしまってて書けたという感じ・・。ところが!
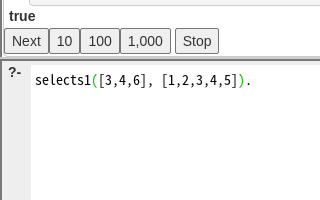
おいっ!自作Selectsちゃんと動いてないぞ。考えられるのはSelectの書き方が違っていた例のアレ

Select部分をお手本に変えてみると
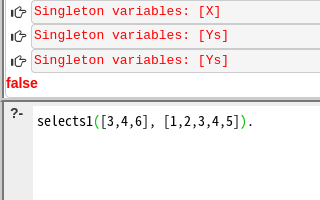
うーん、やっぱりね。不思議だ・・・ とりあえず明日はこの続きからってことで
2024/03/21 Prolog復習、コレだ分かってないのは

Reverseを再び作ってみる上が自作、下がお手本
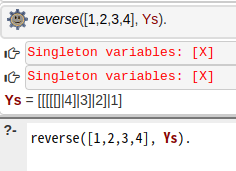
リストを統合しないといけないのでAppendを使わないといけなかった(前も同じことを間違ってたと思う)。
とにかく :- 以降の部分は同列のAndってのは嘘っぽくて常に左側が先に評価されるので右に出てくる変数を予め左で束縛しておかないといけない、んだろ。一方、Head部分で求めたい部分(自由変数?)はBody部で最終的に束縛して返す・・というイメージでいたらエエんでは無かろうか?

つづいてLenghを作ってみて、問題になってる部分を見つけた。ココよココ!
TakeではBody部でまずはN1を更新束縛してから再帰、Mylength(のお手本)では、再帰をしてからNを更新・・これで混乱してたんだ。
見つめてみると・・パターンとして
・最終的に求めたい自由変数が更新束縛Nパターンの場合(上のMy_length)、再帰をした後にNを更新。
・最終的な値を求めるための要素として値を更新したい場合(上のTake)は更新をした後に再帰を行う。
という事が考えられそうだ。とにかくBodyの最後に出てくる部分はHeadで求めたい自由変数部分を返すパーツである!という仮説を元に復習を続けていこうと思います。
2024/03/20 Prolog復習

今日はRemoveから行くか・・
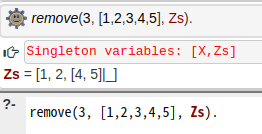
そして今日も失敗するw なんで?

あ、そうか。終了条件の3つ目は初期値だからLsだけで良かったのに、1つ目のルール足すような意識が残ってたのだ


その後、練習問題をやっていく。実はこれらは自分で出来ました。一周目よりは進歩している・・問題はルールが複数ある場合やな・・早く再挑戦したいぜ
2024/03/19まで
話題その1 Prolog復習
風邪がマシになったので学習を再開してるんですが、ちょうど良いから最初から復習をしてみる

既にFizzbuzzを忘れて書けなくなってるしw まあ、初回見た時よりはシックリ来るようになってるかな・・

例えばInsertを自分で書いてみたけど動かない。下が正解。
あ〜正解1行目で引数3、ここが分かってないなぁ。この段階で既に組み立てが出来るわけか・・。上の自分スタイルでなんとか動かせないか?と色々とやってみたが・・

うーん、Writeで無理やり出力しようとしても無理だった。Schemeの時にもよく似たような学習スピードだったし、まあ、いつかは何とかなるだろう
話題その2 大戦略誕生秘話
こんなページが!良いところで終わってるのが悲しい。
大戦略のUIとかルールって、あんまりにも洗練されてたから触ってすぐに「当たり前」として受け取ってしまったけど、色々と物語があったんだなぁ(初光栄ゲーだった三国志2の方が慣れるのに時間がかかった)。
しかし「機械語で書くのが当たり前だった」とかホント気が遠くなる
2024/03/13 お気楽Prologの続き

もしやと思って一応確認。ルール内のBodyはAnd関係なので順番は関係ないけどルールそれ自体はひょっとして順番が関係あるのか?と。
あるとのこと。気に留めておこう

うーん、ムズいw ちょっと日本語訳してみるか。
1:Selectsの終了条件、XsがNullったら終わり
2:例えば[a,b,c],[a,b,c,d,e]だった場合、Selectにa, [a,b,c,d,e] となってYs1がbcde、Selectsにbc, bcdeとなって再帰、XsがNullまで行けたらTrueで途中で脱落したらFalseってことか!Ys1がSelectの段階で束縛されるってのがポイントだな〜

直積集合って何? あ、組み合わせの事か。うーん、どうすればいいか分からん
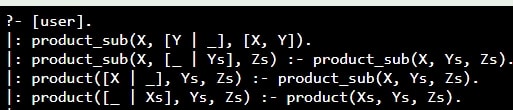
ということでいきなり解答を見る。補助関数がいるのかよ〜。とりあえず日本語訳する
1:補助関数Sub、XとYsのCarであるYをペアである(ファクト)。XはProduct本体からXsのCarを引数にして呼んでくるつもりだろう
2:Subの第2引数YsのCdrで再帰
3:Product本体、XsのCarを取り出してSubにまわしてペアを作る
4:Product本体の再帰、XsをCdrで再帰
ん〜?なんかちょっと分かってきた気がするぞ?というか日本語訳する作業がすごく効果があるんじゃないか?とりあえず自作するとか抜きにしてひたすら日本語訳してみるか・・

超基本的なことを聞いてみる。なるほど・・ファクトとルールを曖昧にしていたな・・問題が明確になった(修正できるとは言ってない)

Procuctの別解。コッチのほうが馴染みのある形式
1:SubでYsのCarをXとペアにしてZsにConsする・・ってのを再帰
2:Subの終了条件、YsがNullったら終わり
3:Procuct本体、XsのCarを引数にしてSubを呼び出してZs1に束縛。Procuctを再帰、Zs2として最後に合体させて本体のZsとする
4:終了条件

べき乗集合・・分からないけど、どうやら部分集合の集合らしい

もちろんいきなり解答を拝見。日本語訳を試みる
1:XsのCarをYsにConsってのを再帰
2:XsのCarが何であっても再帰
3:終了条件
・・なんでコレで冪集合が出来るのか謎なんだが?
1:a,b,c,dでやるとして・・[b,c,d], [a | _] [c,d], [b,a] [d],[c,b,a] [], [d,c,b,a]
2:これが分からん・・

Nextで次の候補が出ると(今知った)
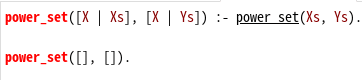
謎の2行目を取り除いてみると
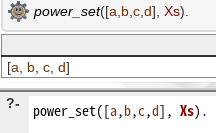
次の候補を求められなくなってしまう

うーん・・なるほど。1行目で再帰した段階で1行目にマッチしないので終わってしまうのか。
で、1行目で作られたYsをそのままにXをCdr・・あれぇ?うーん、今日はここまで。明日考えます!
2024/03/15
昨日から久々の風邪でぶっ倒れてまして・・今日も短時間だけしか出来ませんでした。
1行目をまずは最後まで再起でabcde・・それで終わるやん。2行目は無条件でYsが返るだけなんだし、その前に全部再帰してるからNullって終了条件だしなぁ・・

Claude先生に聞いてみる。ふんふん・・
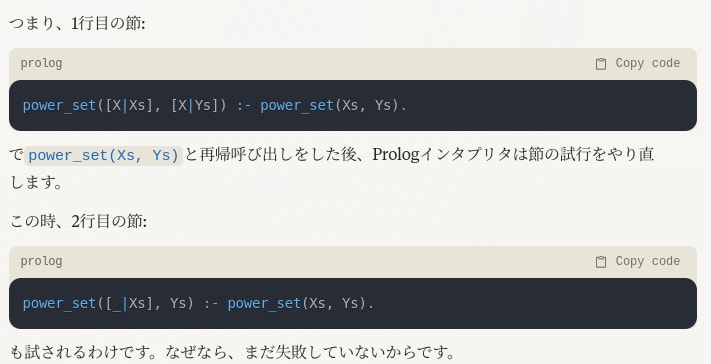
??

何ぃ?もしかしてルールって1つの値に対して全部実行されるってこと!?

ゲーッ!そういうことか〜・・想定してるような動きに全くならないワケだよコレは。やっぱり根本的なところで間違ってたか。
おお〜・・ちょっと全然頭が働かないので風邪が良くなってからになるけど、今までのところでルールが複数(終了条件以外)あるのを見直して値の動きを追ってみることにします。