お昼の「順番を大事に」を胸に夜はヒットの彩花様チャレンジ
先週ヒットで惨敗を喫してますので、今回はお昼の流れで制覇したいと思います。
相棒とBOX組んでレーン抽選へ
二人組が2組(伸さん、さーちゃんと)引いてきた札は25番、、、
何と隣の26番は伸さんたちじゃないですか?ってことはBOXは決まってて右か左か決めただけ???なんとも疑問の抽選でした(笑)
お昼の流れでBB選択してスタート。
今日はピンが良く倒れるわ。(やっぱりBOXによるみたい)
ちなみに前回苦労した箱にはウロパク君が入ってたけど、、、やっぱり同じような結果になってたと。。。
1G目:234スタート
2G目:225でスタートで大きく失速した彩花さんには2Gで80ピン位は勝ってるから今日は楽勝!
って、3G目。オイル変化激しい!!で176と失速。
えーい、最後はフィジックスじゃ。ってボール交換⇒これが裏目に。。。
4G目はスプリット5個(途中3連発含む)
全然アジャスト出来なくってアジャストできたのは9フレから、、、遅かりし。
しっかり逆転されましてん彩花さん
まあ159ではアカンでしょ。
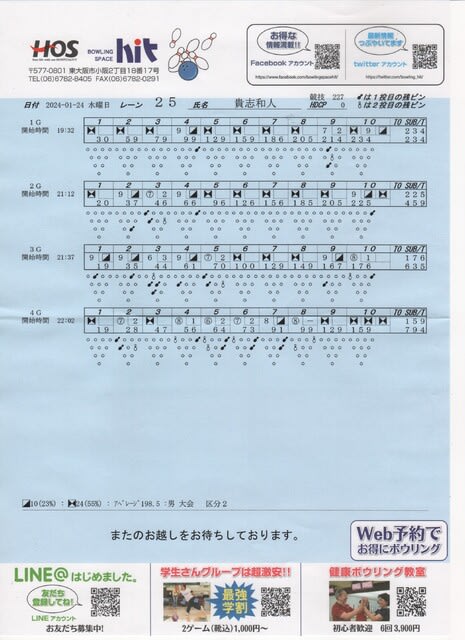
楽勝で900って思ってたら最終的にマイナス打ってました(笑)
ただ、20位の飛び賞当り。
ボールチェンジはちゃんと性格も熟知して考えよう!!
BB⇒フィジックスの流れは初体験だったので収拾付かなかったな



















