速さをみはじの図で教えることの是非

突然ですが、速さって何ですかね？

いろいろな答えがありうると思います。

「君の名は。」で未曾有のヒットを飛ばした、新海監督が10年くらい前に作成した映画

「秒速5センチメートル」のキャッチコピーは

「どれほどの速さで生きれば、きみにまた会えるのか」

でした。

ちょっと哲学的ですよね。



今日は、速さの学習のお話です。

ここで言う速さとは、古典力学における速さでして

「単位時間あたりの、物体の移動距離」

のことです。

哲学的・文学的なニュアンスは一切排除して下さい。

なんで？と言われても困ります。

昔の偉大な学者達が、「速さってのはこういうもんだ」という風に決め、後世の私達がそれに従っているに過ぎません。

難しい言葉で、「定義する」と言います。

つまり、速さとは、単位時間あたりの、物体の移動距離であると定義されたのです。

私は、定義という表現は中学生にはふさわしくないと思っているので

「こういうもんだということにしよう、って昔の偉大な人たちが約束したの。

我々はその約束されたルールに従っているだけだよ。」

と説明しています。



この定義を、ちゃんと数学的に式で表わそうとすると、ベクトルが出てきます。

なので、小学校の算数ではそのような難解な表現を回避するために

「速さ＝距離（道のり）÷時間」

という風に表現し、子どもたちに教えます。

例題です。

名無し先生は、自宅から60km先の遊園地まで、車で移動しました。移動には、2時間かかりました。

名無し先生の乗っていた車の速さを求めなさい。

答えは

60[km]÷2[h]＝30[km/h]

であり、時速30キロメートルとなります。

さて、この速さの話を理解すると

・距離と時間から速さを算出する問題
・距離と速さから時間を算出する問題
・速さと時間から距離を算出する問題

この3パターンに対応出来るようになります。

というか、できるようにならないといけません。

現状、そのように定められています。

そこで、しばしば登場するのがこのみはじBOXです。

（正式名称は知りません。様々な呼び名があることでしょう。ここではみはじBOXと呼びます。）





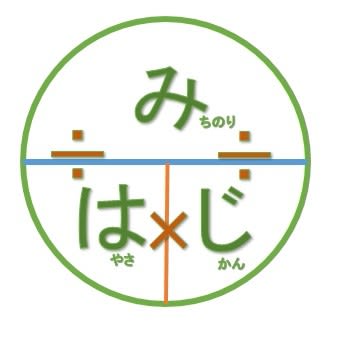
今日は、こいつを理科教師の視点で糾弾します。

私は、こいつが大嫌いです。

なぜならば、「速さとは何か」を理解しなくても、速さの問題が解けるようになってしまうからです。

この図を使うと

問題文から、みちのり・はやさ・じかんの3要素のうち、2つを読み取る。
→この図にあてはめる。
→機械的に、式が完成する。
→かけ算ないし割り算を行なう。
→答えが出る。

という、あまりに思考停止な解き方が成立してしまうからです。

そして最も恐ろしいのは

速さとは何かをちゃんと理解した子も、理解せずに機械的に問題を解いているだけの子も、どちらもそこそこ良い点を取れるようになってしまうので

「本当は理解していない」ことが見落とされたまま

「いい点取れたね、頑張ったね」と次に進んでしまう可能性があるのです。

そのような子は、中学の理科で間違い無くつまづきます。



中1の2学期で、密度の学習があります。

密度とは、単位体積あたりの質量のことです。

○○あたりの××……どっかで聞いた覚えがありますよね。

ちゃんと速さとは何かを理解してきた生徒は

「なんだ、速さと似たようなもんじゃん」

で終わります。

ところが、速さの計算をみはじBOXに頼りきってきた生徒は、フリーズします。

体に染みついたルーティーンとは異なるからです。

（ちなみに、みはじBOXを使用して速さの計算を行なうことすらできない生徒は、この時点で詰んでいます。
私の経験上、クラスに数人はいます。
ですから、すべての生徒に同じ内容の授業を受けさせることは、以前から主張していますが、教師・生徒双方にとって不幸なことだと思います。
今日は、話の本筋から外れるので、これ以上の議論はしませんが。）

また、密度の計算を学習するころには、数学での方程式の学習が完了しています。

このへんは、教科書ってよくできているなぁ、と思います。

すなわち

密度＝質量÷体積の式を暗記し

既知数は代入、未知数をxとおき、方程式を立て、未知数を導出すると言うことができるようになります。

そして、密度でこのやり方を身につけておかないと、次の質量パーセント濃度で苦労します。



みはじBOXの

みちのりを質量に

はやさを密度に

じかんを体積に書き換え

同様のBOXを作って暗記することは可能です。

しかし、それをやってしまうと、後に大変な目に遭います。

まずは、質量パーセント濃度。

質量パーセント濃度は

質量パーセント濃度＝（溶質の質量/溶液の質量）×100

です。

この×100があるため、これをBOX化すると逆にややこしくなるのです。

そしてさらにその後、圧力の計算や、フックの法則等

数学的処理を要求する学習内容は多く存在します。

すなわち、BOXでの処理は、その場しのぎにはいいですが、本質的な理解・学力向上には寄与しないと思います。



またまた長くなってしまいました。

言いたいことを短くまとめると

・みはじBOXによる速さの指導を行なうと、速さを理解しなくても問題が解けるようになってしまうので、児童の理解不十分を見落とす可能性が高い。
・理解不十分なまま、みはじBOXで答えを出すことになれてしまった生徒は、中1理科でえらい苦労をする。
・よって、みはじBOXで授業を行なうのは、いかがなものか。

です。

というか、こういうリスクがあるから、教科書に載ってないんじゃ無いの？と思います。

それを、「教科書にないウラワザ」的に、嬉々として教える教師や塾講師は安直ではなかろうか、と思います。