自己診断に 向けて 購入図書を活用して分析してみました。
今回発見した図書は 自己診断に ふさわしい 参考図書として 質的分析してみました、その方法とは・・・
・・・・・・・・・・・ 統計の図書を購入して ・・・・・・・・・・・・。
計学を学んでいらしゃる読者の皆さんの中に、「学びの完熟度」が気になりませんか。
学び途中の私は 特に気になっています、例えば学びの手順は時系列 これでよいのか?? 基本的の学びの深度はこれでいいのか?? 基礎がまだ未成熟なのに R言語に目移りして迷走している状態です。
昨日(2017/12/08)にJR大阪駅付近某書店にて 自己診断(基本的内容)を行うに ふさわしい新刊「統計入門書」発見したのでした。
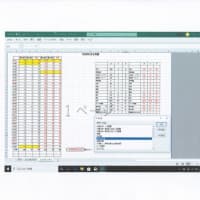
その図書の目次の数値データを別表に転写整理する 単元の頁を可視化(グラフ)することで復習箇所を絞ることで自分の習熟度に役立ててみました。
発見した「入門書」について 失礼ながらページ分析したくなりました、以下添付資料はは単元ごとの頁数です 例えば統計A図書では 単元2で63頁の説明 そして始まりp56からp121の頁を使っている 赤のシールをご覧ください。

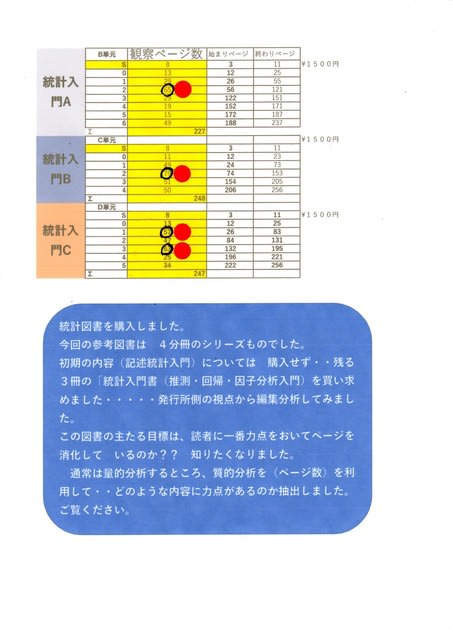
添付説明に追加ご説明します。
図書(統計入門A)で特化して記述すると、この本は¥1500円で総ページ数は 227ページ、目次では 単元毎に→さらに細目されていて・・赤丸シールでご説明すると・・2単元65ページで構成されています。
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
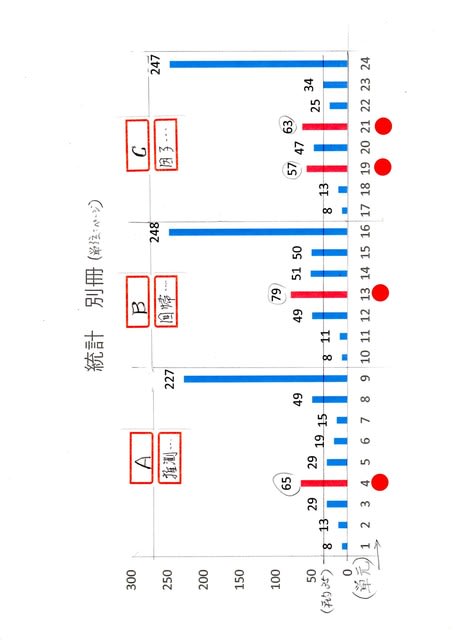
前記述の目次データを 別表を可視化 グラフにしてみました。
グラフご説明:別冊A の棒グラフの赤は 4単元中 65ページあります、8項では12頁を使って正規分布の説明が掲載してあり「二項分布の極限が・標準正規分布になる」ことを確認することが出来ました。
:::::::::::::::::::::::::::::::::::::
また 別冊C つまり統計入門C に飛びまして「分析結果をどのように解釈するのか」
さらに 「数量化3種 アンケート」 等が掲載されています。
残念ながら 果実はあまり熟していませんでした、 もっと勉強が必要と判断しました「恋する統計学」のお力をかりて頑張ります。
反省の箇所を細目表現すると・・「因子分析が 私自身 浅かった」と感じています。
::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::

◎
この図書の感想は・・・・教科書の部分に触れながら これまでにない・・「統計とは・・・ について 浅く広く」論じていることが 学ぶ者にとっては 良き文献であると 感謝しているところです。
ありがとうございました。
投稿者 統計の猿 より29年12月14日
コピー 検索に貼り付ける。
http://www.stat.go.jp/teacher/c2learn.htm#materials
今回発見した図書は 自己診断に ふさわしい 参考図書として 質的分析してみました、その方法とは・・・
・・・・・・・・・・・ 統計の図書を購入して ・・・・・・・・・・・・。
計学を学んでいらしゃる読者の皆さんの中に、「学びの完熟度」が気になりませんか。
学び途中の私は 特に気になっています、例えば学びの手順は時系列 これでよいのか?? 基本的の学びの深度はこれでいいのか?? 基礎がまだ未成熟なのに R言語に目移りして迷走している状態です。
昨日(2017/12/08)にJR大阪駅付近某書店にて 自己診断(基本的内容)を行うに ふさわしい新刊「統計入門書」発見したのでした。
その図書の目次の数値データを別表に転写整理する 単元の頁を可視化(グラフ)することで復習箇所を絞ることで自分の習熟度に役立ててみました。
発見した「入門書」について 失礼ながらページ分析したくなりました、以下添付資料はは単元ごとの頁数です 例えば統計A図書では 単元2で63頁の説明 そして始まりp56からp121の頁を使っている 赤のシールをご覧ください。


添付説明に追加ご説明します。
図書(統計入門A)で特化して記述すると、この本は¥1500円で総ページ数は 227ページ、目次では 単元毎に→さらに細目されていて・・赤丸シールでご説明すると・・2単元65ページで構成されています。
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
前記述の目次データを 別表を可視化 グラフにしてみました。
グラフご説明:別冊A の棒グラフの赤は 4単元中 65ページあります、8項では12頁を使って正規分布の説明が掲載してあり「二項分布の極限が・標準正規分布になる」ことを確認することが出来ました。
:::::::::::::::::::::::::::::::::::::
また 別冊C つまり統計入門C に飛びまして「分析結果をどのように解釈するのか」
さらに 「数量化3種 アンケート」 等が掲載されています。
残念ながら 果実はあまり熟していませんでした、 もっと勉強が必要と判断しました「恋する統計学」のお力をかりて頑張ります。
反省の箇所を細目表現すると・・「因子分析が 私自身 浅かった」と感じています。
::::::::::::::::::::::::::::::::::::::
::::::::::::::::::::::::::::::::::::::


◎

この図書の感想は・・・・教科書の部分に触れながら これまでにない・・「統計とは・・・ について 浅く広く」論じていることが 学ぶ者にとっては 良き文献であると 感謝しているところです。
ありがとうございました。
投稿者 統計の猿 より29年12月14日
コピー 検索に貼り付ける。
http://www.stat.go.jp/teacher/c2learn.htm#materials















※コメント投稿者のブログIDはブログ作成者のみに通知されます