標準偏差値を利用して(代入して)標準化の出し方を復習してみました。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
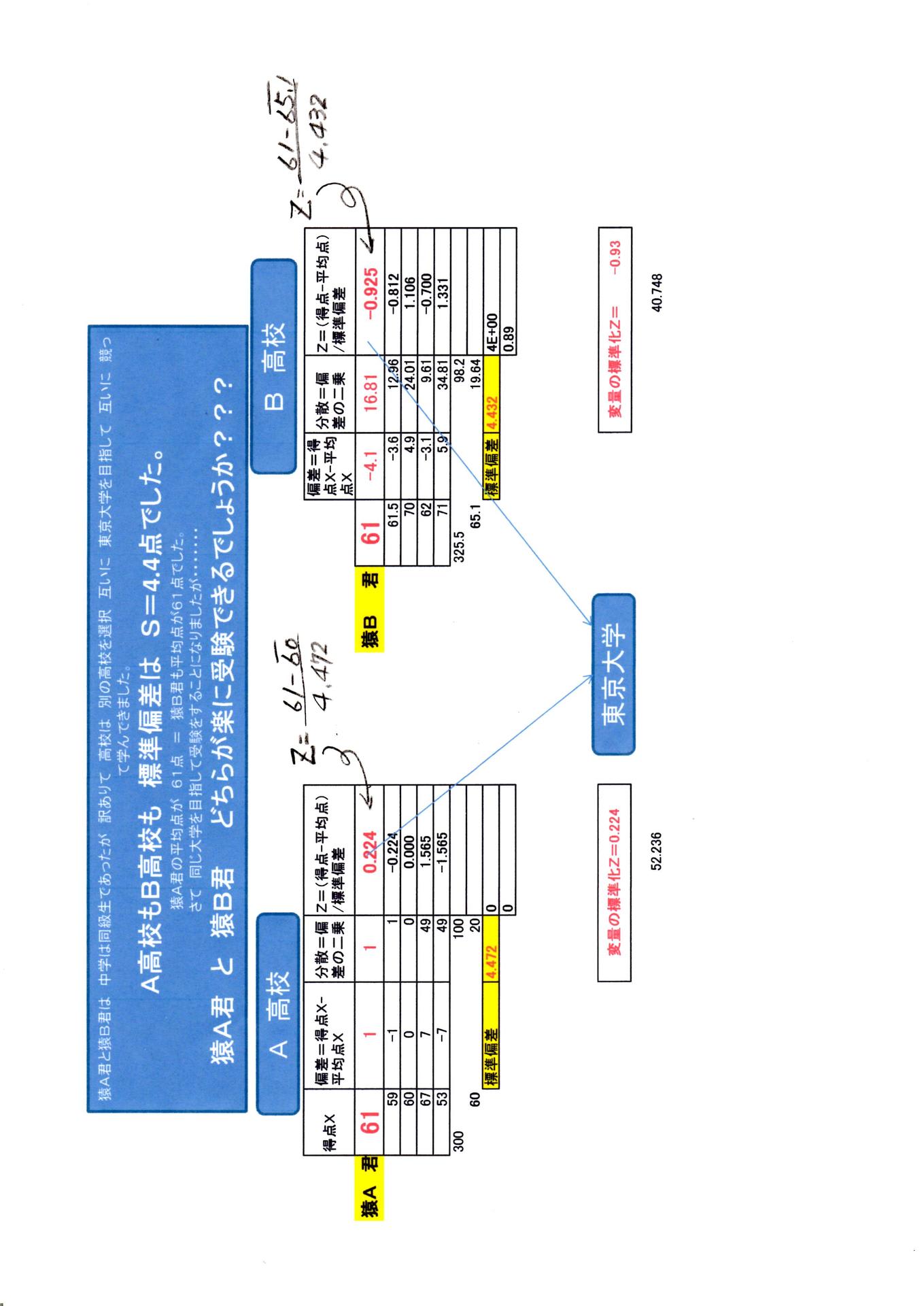
お子さんを お持ちの お母さんから 別紙のような質問がありました。つまり 簡単に言うと「A君とB君は中学時代は同じ学校であったが 高校は 訳あり 別々の 高校に通うようになり 試験のたびに 点数を見せ合うことで競っていたようだ それをできなくなりました。 この春の「大学入試センター試験」を受験したようだ。
しかし A高校の平均点61点の「猿A君」と B高校の平均点61点の「猿B君」との両校の学校の 標準偏差値 はほぼ同じで 4.4点 であるという。両君は 大学進路選択に迷っていました。
さて どのように 説明をしたら 良いでしょうか・・・・・という悩みです。

高校が違うと 難易度が違い比較することが 例えAB君が61点として 同じ実力と錯覚し進路判断には 困難ではと 思われます なぜなら「偏差値や学生さんのテストの平均点が同じでも」A高校の全生徒の平均点が違うと 「標準偏差を求めるにあたり 平均値からの離れ つまり 偏差が違うことを学びました」ことを 思い出しました。
よって このような 母集団(学校)が 違うときは 共通な「升 マス」の中に入れる必要があるのでしょうかね!!。よって余り自信がありませんが 両高校の「高校の偏差を」1イチ を 100%になるように正規分布に いわゆる標準偏差化(化)に加工することで数値化できる方法が考えられます。
<一度試してみます>
①正規分布図において 平均値を ゼロ:0 とし さらに 標準偏差値は イチ:1とする必要がいります。
②別紙 のA君の 偏差化(0.22)となり B君の 偏差化(-0.92)となります、この意味は 平均値からの離れを数値化して表現しています(正規分布図)よって 見えるのは 比較して AB君の間に -0.92<Z=0.16(比較者間)<0.22 に多少の開きがみえます。あとは ご本人の意思決定ではないでしょうか? 余談ですが 株式において2社比較するにあたり 株価は同じでも 出来高が 違うまたは 利益率等が見えないに類似して??
③その公式は Z=(X - 平均X) ÷ 標準偏差値 ・・・である。最後尾に貼り付けあります。
④参考に:標準偏差値 の 代入応用は これからも 良く使われています。最後尾に「センター試験の結果」がホームページで告知されましたので 一度 開いて見てはいかがでしょうか。


 一度教科ごとの 実力を 比較 試算してみては 如何でしょうか。
一度教科ごとの 実力を 比較 試算してみては 如何でしょうか。
余り 自信が ありません 読者の方で 「検証」してから お使いください。 統計家を志す猿より。



































