近年データをもとに回帰分析の手計算部分を 省略でき PCプログラムで簡単に解決できるようになりました。
その前に見えない、ここでいうブラックボックスとは、どんな意味かご説明しましょう、例えば 円周率の3.14の根拠を知らず義務教育で使っていましたが(トンネルの中には高校で学ぶ)微分法で証明解読でき納得した経験がおありと思います。つまり答えは「出力されるがその経緯」がわからない事をここでは言っています。
あまり便利過ぎて本質が不明のままだと顧客から「なぜ」の質問があったときに対処するのに御説明が出来ません。ブラックボックスの疑問に挑戦して何故このように分析できるのかをより深めてみました。一例をご覧ください。
別紙1は 分析用のサンプルデータですが、回帰分析を実施してみたいと思っています。(7月29日のレポート表を再掲)
分析用のサンプルデータですが、回帰分析を実施してみたいと思っています。(7月29日のレポート表を再掲)
別紙2は サンプルデータでは数字の乱立ばかりですので 良く解りません よって まず目で確認出来るようにグラフで可視化してみました(このような可視化表現は中学校で教えられています)
サンプルデータでは数字の乱立ばかりですので 良く解りません よって まず目で確認出来るようにグラフで可視化してみました(このような可視化表現は中学校で教えられています)
別紙3は グラフの回帰直線に、周辺データを 近似曲線として表現出力してきました。ぼちぼち このグラフが使えるかどうか教えてくれたのです、検証してみましょう(決定係数R2=0.09で あまり採用したくありませ(R2=0.5以上を採用)のでパスすることにしました。でどうするの?「PCの分析ツールを操作して視点を変えて回帰分析を試みてみましょう」
グラフの回帰直線に、周辺データを 近似曲線として表現出力してきました。ぼちぼち このグラフが使えるかどうか教えてくれたのです、検証してみましょう(決定係数R2=0.09で あまり採用したくありませ(R2=0.5以上を採用)のでパスすることにしました。でどうするの?「PCの分析ツールを操作して視点を変えて回帰分析を試みてみましょう」
別紙4
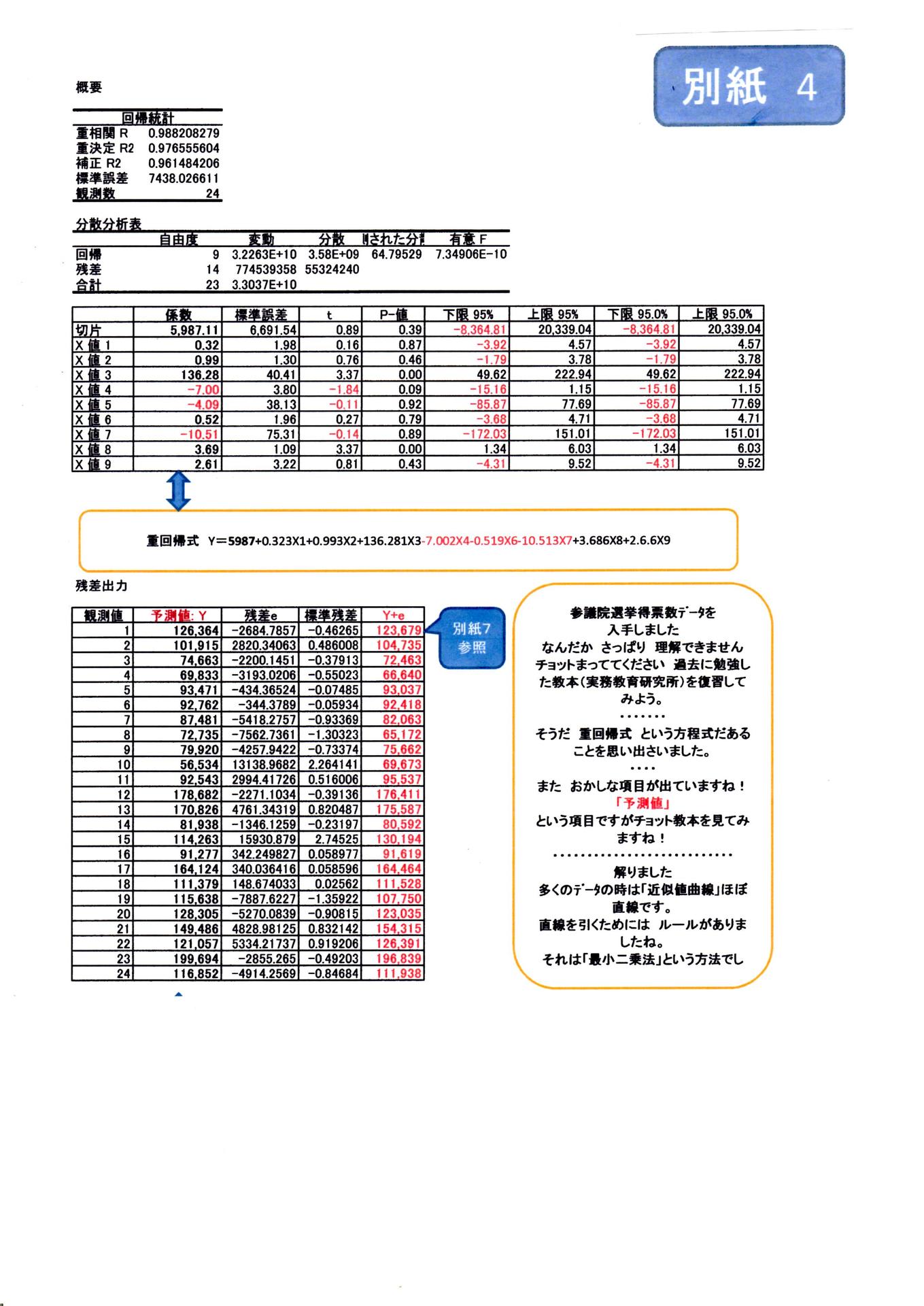
 最近は EXCEL 2010 以降のプログラムにて,ツールで分析できるようになりました、これが(トンネル)で直接 計算せずとも 分析してくれます。分析結果は別紙4が分析結果です。
最近は EXCEL 2010 以降のプログラムにて,ツールで分析できるようになりました、これが(トンネル)で直接 計算せずとも 分析してくれます。分析結果は別紙4が分析結果です。
しかし計算過程がブラックボックスに入って皆目わかりません、これでは 他のお人にご説明が出来ません(財団法人・実務教育研究所の教本で教えてくれます)。 例えば出た回答の中に「係数とは、切片とは、予測値とは、残差とは、P値とは、有意とは・せめて出力表の意味について教本復習しておきたいと思っています。
http://www.jitsumu.or.jp/index.php(財団法人・実務教育研究所の教本で教えてくれます)。
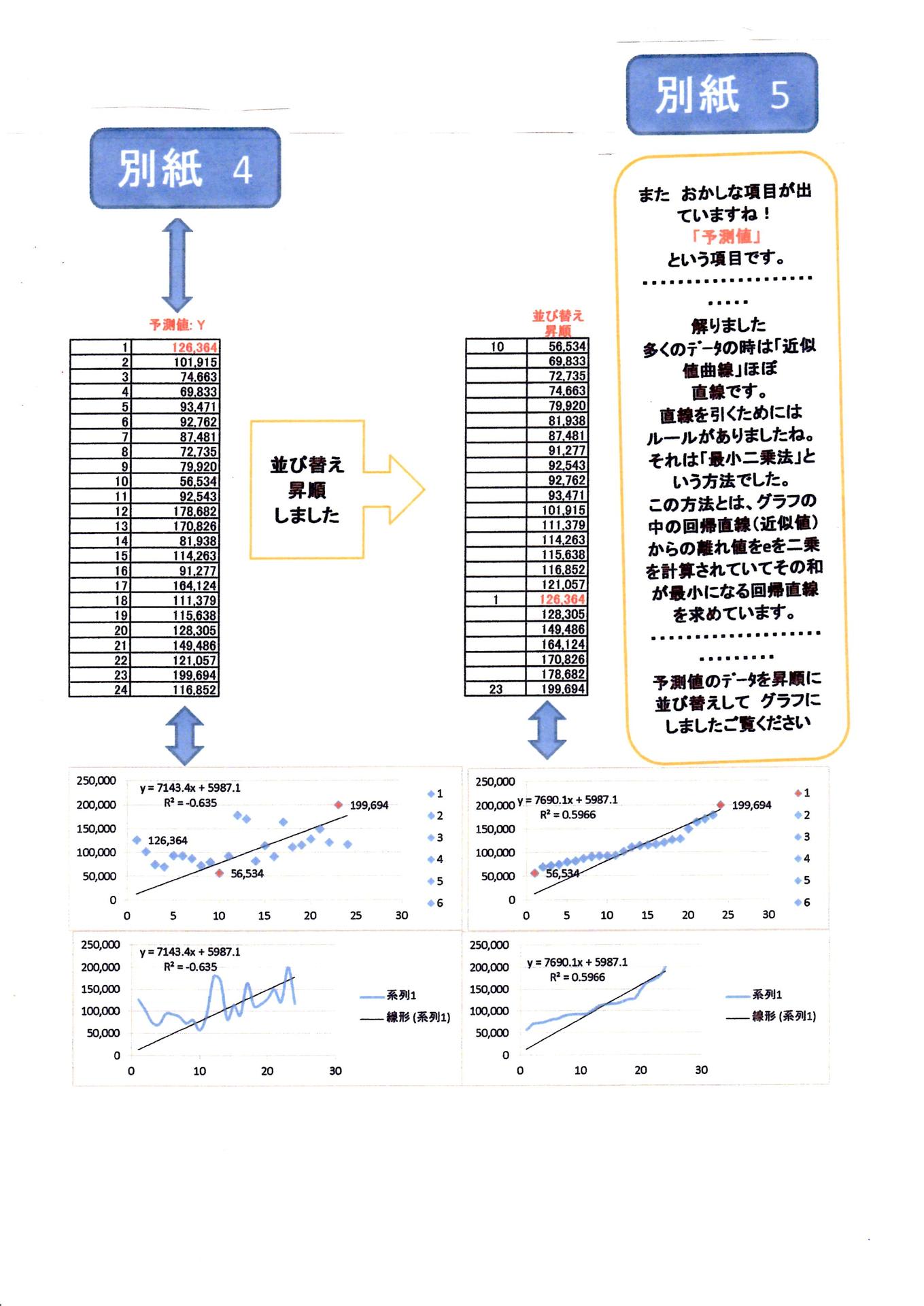
別紙5 予測値(Y=)の出力している「意味は回帰曲線の値でしたね」また 並べ変えるて昇順することで 連続性の点で表示しましたから、新たな発見に お気付くこととなりました。回帰曲線の決定係数はR2=0.5966ですから信頼できます。
予測値(Y=)の出力している「意味は回帰曲線の値でしたね」また 並べ変えるて昇順することで 連続性の点で表示しましたから、新たな発見に お気付くこととなりました。回帰曲線の決定係数はR2=0.5966ですから信頼できます。
別紙6 残差とは、どんな仕組みでしょうか、詳しく教えてくださる著書を発見しました、下記別紙をご覧ください、基本の勉強を後押しできる よい本です。
残差とは、どんな仕組みでしょうか、詳しく教えてくださる著書を発見しました、下記別紙をご覧ください、基本の勉強を後押しできる よい本です。
「係数とは、切片とは、予測値とは、残差とは、P値とは、有意とは・の疑問に答えてくださいます」(著者・日花弘子・EXCEL統計解析入門・2分冊別々販売中)
追伸 著書「高校生からの統計入門・加藤久和」の本は統計とは・・にこたえる教職員向けには易しすぎる内容です、私・統計の猿 にはちょうどよい著書では統計学の骨格の説明です、枝葉の部分には簡単に記述されています、私(統計の猿)は、学ぶ者の現在位置に活用しています。

別紙7 回帰関数を作成にあたり、2方法を試みてみました、①分析ツールから導き出す方法と②Exce関数・LINEST・から導き出す方法を見比べてみてください①=②とは一致しました。
回帰関数を作成にあたり、2方法を試みてみました、①分析ツールから導き出す方法と②Exce関数・LINEST・から導き出す方法を見比べてみてください①=②とは一致しました。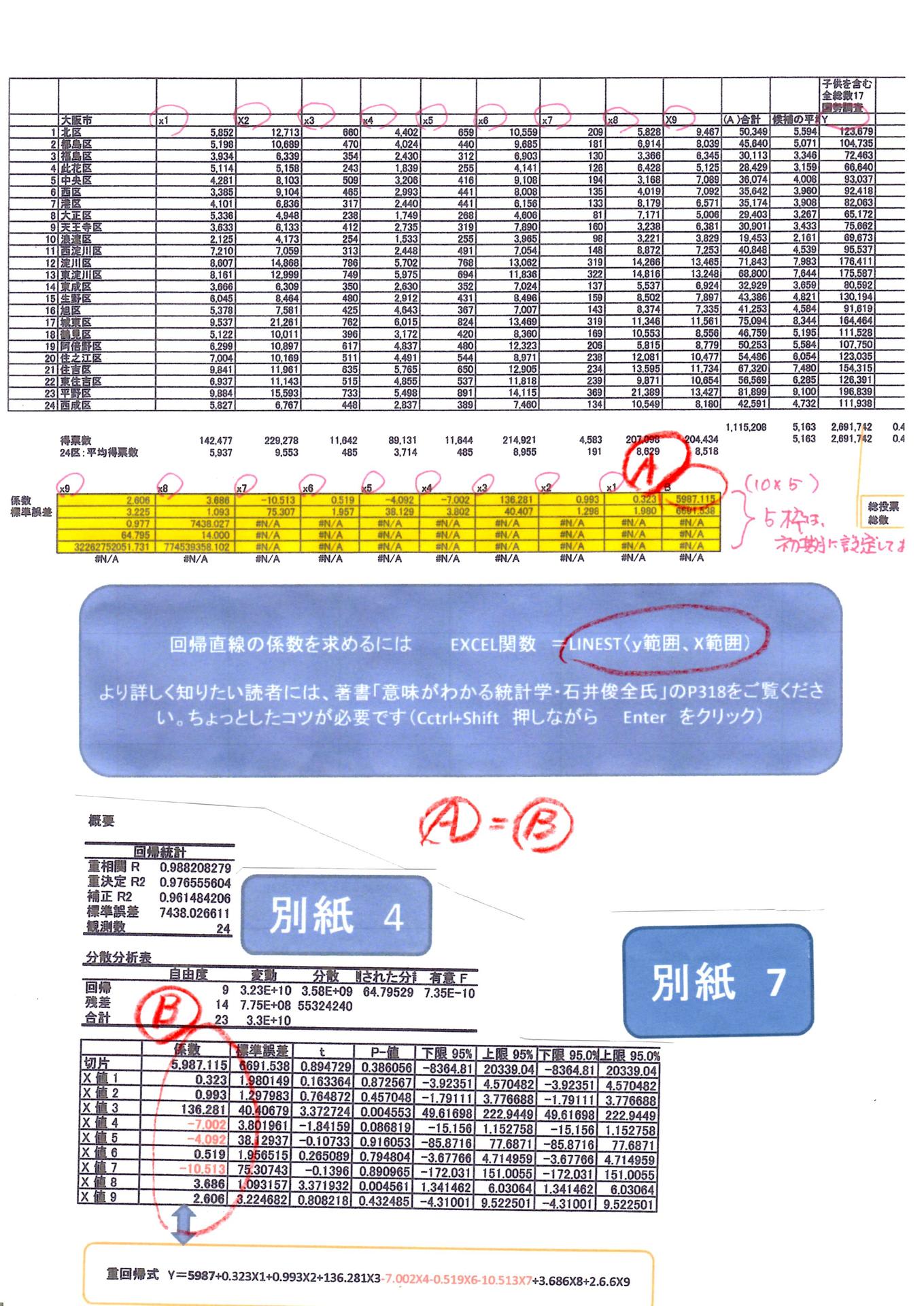
以上









