Ｅｘｃｅｌ ・統計関数STDEV ・ を使って「標準偏差」を求めてみました。

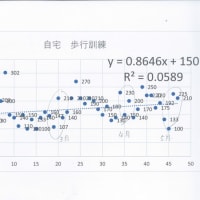
４月８日の日記に掲載しました　筆記による　基礎計算（標準偏差）との　比較をしてみました。

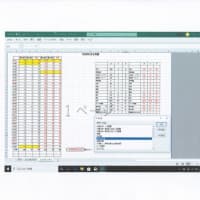
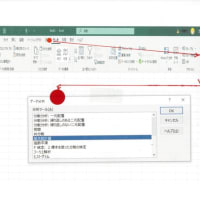
①　統計関数である　Ｅｘｓｅｌ関数での方法を　復習してみました　別紙をご覧ください。

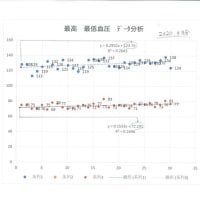
②　筆記計算と、Ｅｘｃｅｌ統計関数＝ＳＴＤＥＶ（ｘ1～ｘn）方法　との　結果比較表をご覧ください。

③　感想1：標準偏差の筆算では　計算根拠が　良くわかりました。これで　標準偏差の計算が出来るようになりました。

④　感想2：今後統計関数ＳＴＤＥＶ（　　、　　）区間方法で簡単に求めれるようになりました。

④　今後は　標準偏差値が　大きいほど　平均値から　分散（離れている）。また　標準偏差値が小さい程平均値に集中していることを　　復習したく思っています。調査目的が　道路の混雑度であるなら　標準偏差値は大であれば　良くすいていると解釈できます。

つまり正規分布図で説明がつくのです：例（標準偏差=２７台）の時は　平均値112.4-27＝85.4台です、　　又は平均値112.4+27＝139.4台　となります。つまり正規分布図の85.4～139.4の間に　現場調査をしました交通量調査の３分の2のサンプルがあることに解釈できるのです。視点を変えて学校の成績がこの範囲にあれば　クラスのなかで平均点前後にある（位置）とみることが出来ます。下記の表は統計Ｅｘｃｅｌ関数で行った表です　ご覧ください。