皆さんこんにちは。
最近、理科のブログばかり書いている気がするので、
今日は算数と理科にまたがる話をしてみたいと思います。
算数と理科の両方で登場するものの代表といえば濃度の問題でしょ
その中でも今日は、「濃縮」と「希釈」の話をしたいと思います。
「濃縮」というのは、食塩水の水を蒸発するなどのように、
水溶液の中から水分だけを取り除いて、
一方、「希釈」というのは、水だけを加えることで、
ちょうど真逆の作業ですが、どちらも「
たとえば、次のような例題を考えてみてください。
【例題】
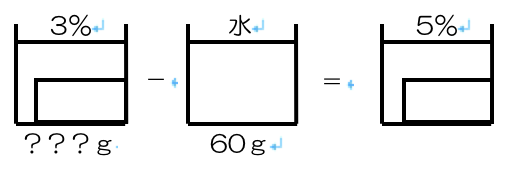
濃度3%の食塩水をにつめて、水を60g蒸発させたら、
3%の食塩水は、何gありましたか。
この問題、苦手な人も多いと思います。
普通に解くと、ちょっと難しいからです。
【普通の解法の例】
3%の食塩水全体の重さを1とすると、
その中に入っている食塩の重さは0.03ということになります。
ここで、水を蒸発させても、
5%の食塩水の中に入っている食塩も0.03です。
5%というのは、分数にすると20分の1ですから、
食塩水全体の重さは、0.03とおいた食塩の重さの20倍、
食塩水全体の重さの割合は、蒸発前が1、蒸発後が0.
水を60g蒸発させたことで0.4減少しています。
つまり、この減少した0.4が、蒸発した60gにあたるので、
1とおいた3%の食塩水全体の重さは、
60÷0.4=150(g)
う~ん、やっぱり難しいですね。
「割合」なんて持ち出したら、さらに難しく見えてしまいます。
そこで、ちょっとした裏技
濃縮や希釈のように、水の重さだけしか変化しない場合は、
変化の前後での「濃度」と「全体量」の比が逆比の関係になる
という性質を使ってみましょう。
水を蒸発させたことで、濃度は3%から5%になりましたので、
変化前と変化後の濃度の比は「3:5」です。
水を蒸発させる作業は「濃縮」にありますから、
先ほどの性質を使うと、全体量は「5:3」になりますね。
このときに、減った「2」にあたる量が60gですので、
「1」にあたる量は30g。
したがって、「5」にあたる3%
いかがですか? 簡単でしょう?
この例題は「濃縮」の場合でしたが、
水だけを加えてうすめる「希釈」の場合にも同じワザが使えます。
ぜひ活用してくださいね!