受験算数のコツ！水そうと棒の問題は順逆自在の術！ 大日本国民としてがんばる

6月29日、この中には6と9という上下逆になった数字が入っています。
ということで、今回は「逆にするとわかりやすくなる」という解法をご紹介します。

 

まずは、この問題をご覧ください。

 

問題
 
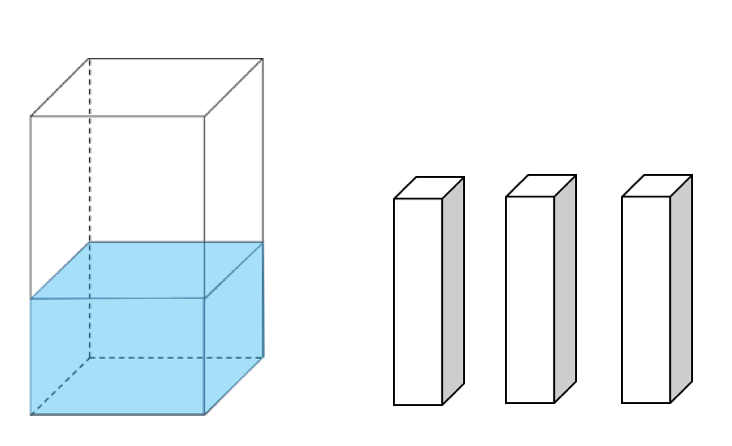
底面積が300㎠の直方体の形をした水そうに、10㎝の深さまで水が
入っています。ここに、底面積が50㎠で高さ16㎝の棒を、床に垂直になる
よう、水そうに入れていきます。

 

 

(1)棒を2本、水そうに入れると、水面の高さは何㎝になりますか。
(2)棒を3本、水そうに入れると、水面の高さは何㎝になりますか。

 

 

この「水の入った水そうに棒を入れる」問題は、いろいろな解法があります。
一つは、棒が押し出した水が移動して、何㎝高さが増えるかを考えるもの。
もう一つは、変化しない水の体積を考えるものです。
今回は水の体積を使って解きます。
ただし、どちらの解法を使うとしても、この手の問題を解くには図が必要。
ここで、今回のポイント！図は順逆自在の術で描こうです。

 

順逆自在の術とはどういうことか？
水そうに入ったものは、①水➡②棒　の順番ですが、
これを、①棒➡②水、というふうに入れ替えるわけです。
結果として、水そうの中に入っているものは同じなので、水面の高さも同じ
ことになります。この逆転の作図の良い所は、水面の高さがよくわからなく
ても、簡単に描けるということです。

 

 

では、(1)を解説していきます。

 

＜STEP1＞　水の量を求める
底面積が300㎠・高さ10㎝の直方体の体積になりますので、
300×10＝3000㎤です。

 

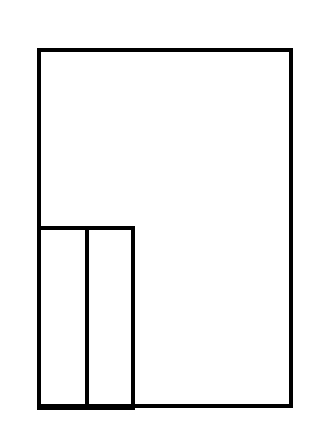
＜STEP２＞　空の水そうに棒を入れる
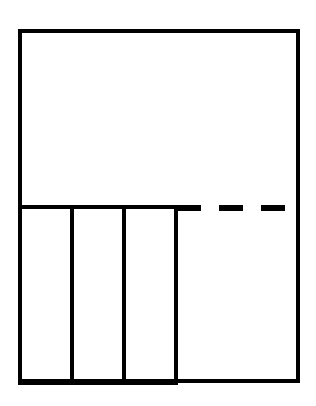
先に棒を入れます。図は水そうを正面から見た図にします。
また、見やすくするため棒は端に寄せておきます。

 

 

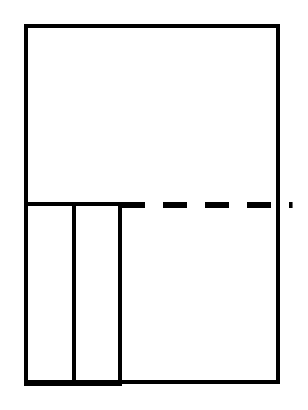
＜STEP３＞　棒の高さの所に点線を書き、点線より下の部分の体積を求める
棒の高さが16㎝なので、16㎝のところに点線を書きます。
ここより下は、棒の底面積だけ水が入りませんので、水が入る部分の面積は
300-100＝200㎠になります。
したがって、下の部分の体積は200×16＝3200㎤と求まります。

 

 

＜STEP４＞　水面が棒より上か下かを判断する
水の体積と、STEP３の体積を比べ、
水の体積が小さい➡水面は棒よりも下にくる➡STEP５－１へ
水の体積が大きい➡水面は棒よりも上にくる➡STEP５－２へ

 

＜STEP５－１＞　水面が下の場合
この場合、水が入る部分の底面積は一定になりますので、
3000÷200＝15㎝　これが水面の高さになります。
したがって、(1)の答えは15㎝です。

 

(2)の場合も考えてみましょう。
STEP１は同じ3000㎤
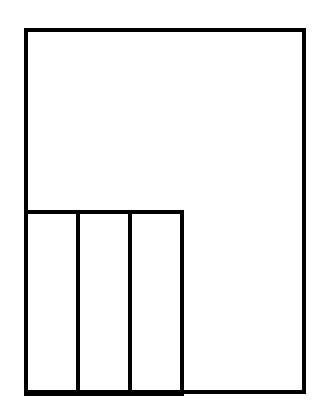
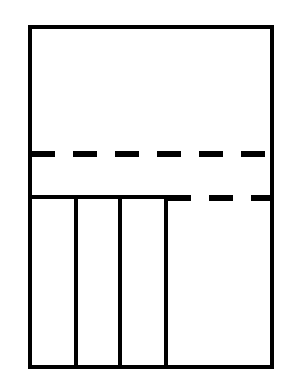
STEP２は下のようになります。

 

 

STEP３は、水が入る部分の面積が、300－50×3＝150㎠となりますので、
150×16＝2400㎤と求まります。

 

 

STEP４は、水のほうが体積が大きいため、水面が棒より上、となり、
STEP５－２へ移ります。

 

＜STEP5-2＞水面が上の場合
STEP３で求めた体積を超えた水が、棒の上に入ります。このときの面積は
水そうと同じ面積になります。

 

 

3000－2400＝600
600÷300＝2
つまり、棒の上に2㎝水が入ることになりますので、水面の高さは、
16＋2＝18㎝と求まります。

 

いかがでしたか。順逆自在の術。
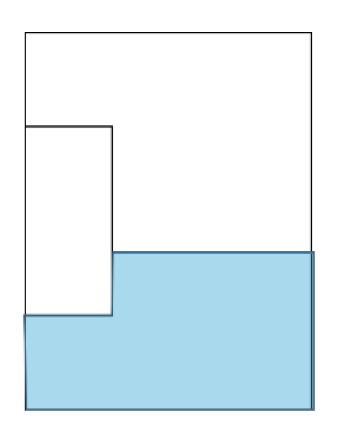
この技は、棒が底面についていない下のような場合でも、問題が解きやすく
なります。

 

 

順逆自在の術には、立体図形でも使えたりします。