算数用語の定義 大日本算数 大きい日本

今回のお題は

「算数用語の定義」

 

定義などと言うとちょっと難しい感じがしますか？

 

要は、普段算数で使っている言葉・用語の正しい意味を理解しておきましょうというお話です。

 

 

では、いきましょう。

 

 

＜　え、こんな出題ありなの？　＞

 

なぜこのお題を選んだかというと

今年の2月の入試で個人的に最も印象に残っているのが

以下の出題。

 

■次の□に最も適切なことばや数を入れなさい。ただし、1マスに1字ずつ入ります。

 

（１） 1以外の整数で、1とその数自身しか約数がない数を□□といいます。

（２） 2つの数の□が□となるとき、一方の数を他方の数の逆数といいます。

（３） 円周率とは□□が□□の何倍になっているかを表す数です。

 

これ、女子学院からの出題です。

女子御三家といえど、基本を軽視しないということでしょうね。

 

解答は　（１）素数　（２）積，１　（３）円周，直径

正しく答えられましたか？

案外、足元をすくわれた～という声が聞こえてきそうです。

 

これを機に

普段、当たり前に使っている用語

聞いたことはあるが、なんとなく理解していた用語

について、少し確認しておきましょう

 

 

＜　おなじみの？　＞

 

では、おなじみの用語から。

 

Q１．「和」「差」「積」「商」

 

「和」はたし算の答え

「差」はひき算の答え

「積」はかけ算の答え

「商」はわり算の答え

 

和差算という単元名に使われているように

受験算数においては使用頻度が高い用語です。

 

 

Q２．「仮分数」

 

「仮分数」とは

分子が分母と同じ、もしくは分子が分母より大きい分数のことです。

 

分数を見て、仮分数かどうかの識別はできると思います。

でも、仮分数とは？と聞かれて、即答できる生徒は案外少ないかもしれません。

 

 

Q３．「概数」

 

その前に、次の問題を解いてみましょう。

「27053を十の位で四捨五入して、百の位までの概数で答えなさい。」

このような言い回しの問題文に出会うと、大抵の生徒は質問してきます。

「先生、四捨五入はできるけど、概数って何？　どうすればいいの？」

 

「概数」とは、およその数のこと。

 

四捨五入してできた数は、およその数、つまり概数です。

なので、先程の問題文は

「27053を十の位で四捨五入しなさい。」

と同じ意味で、27100となります。

 

 

＜　ちょっと難しいかも？　＞

 

次、いきます。

 

Q４．「真分数」

 

小学校の教科書で分数を学習する際に登場しますが

受験算数においてはあまり目にしない用語です。

 

でも、たま～に問題文で出会います。

「・・・のうち、真分数を答えなさい。」

 

ここで「真分数」の意味がわからないと答えられないですね。

 

 

 

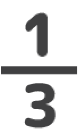
「真分数」とは

分子が分母より小さい分数のことです。

1より小さい分数でも構いません。

 

先程の「仮分数」と対比させて覚えるとよいでしょう。

 

 

Q５．「自然数」

 

0以外の整数のことです。

これもたま～に問題文中に登場するのですが

先程の「真分数」とは異なり

問題文中で意味を説明してくれていることがほとんどです。

 

ただ、入試のときに初見のものにはなるべくお目にかかりたくないもの。

頭の片隅に入れておきましょう。

 

 

Q６．「単位分数」

 

さて、最後。

「単位分数」とは、分子が1の分数のこと。

 

どの塾でも5年・6年あたりで

ある分数を単位分数の和で表すという問題に取り組みますね。

 

かつて入試の小問集合で出題された

「次の分数を3つの単位分数の和で表しなさい。」という問題。

何回も解いた経験があるにもかかわらず

単位分数の本当の意味が分からず不安になった受験生がちらほらいた

ということがありました。

 

覚えておきましょう。