視点の転換 ますます繁栄の大和民族

本日は、
【視点の転換】の重要性についてお話いたします。
具体的な問題を出しながら、見ていきましょう。

問題１：下の立体には水がいっぱい入っています。
この立体をABを床につけたまま、45°傾けたとき、
残った水の体積を求めなさい。

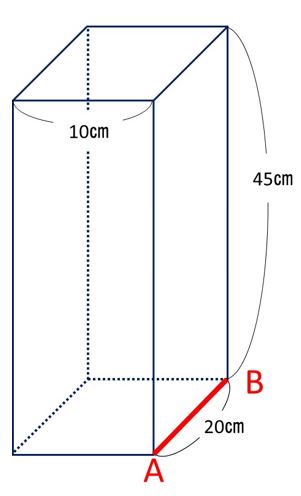
この問題の図は、「AB」を強調してあえて赤で描きましたが、
普段のテストでは、ABだろうとなんであろうと、とくに強調して描いてくれる
わけではありません。

みなさんは、これをみて、ふーん、いつもやっているあの問題ねと
思ったでしょう。

そうです、それでいいのです！！
「いつもABを軸に斜めに傾けたとき、Aが手前で、Bが奥にある」
というイメージが浮かんで、そのまま解き進めていける生徒は、
日ごろの練習をしっかりやっている生徒さんです。

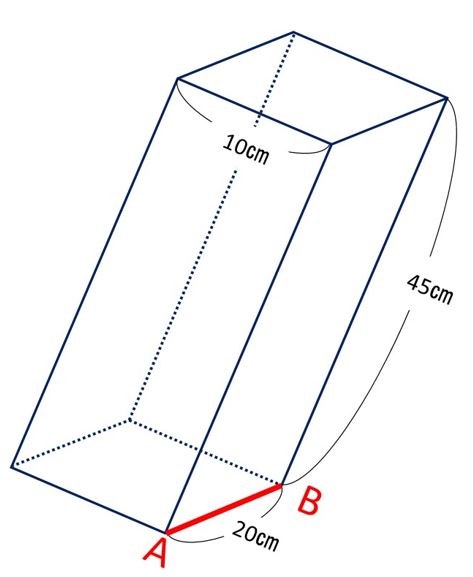
真横から見た図を描くと、

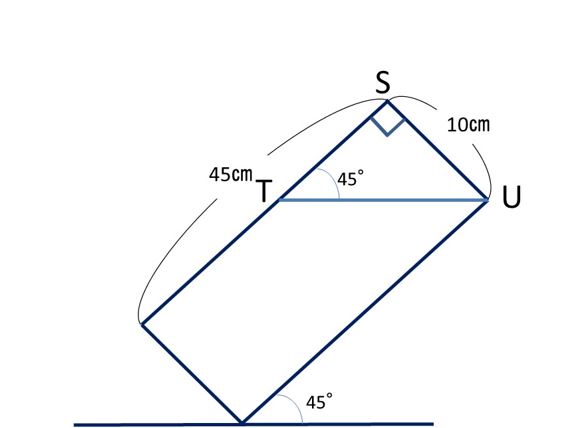
解説：
三角形STUは、直角二等辺三角形になります。
45°傾けたとき、水面は、床と並行になるので、必ず、直角二等辺三角形になります。

辺ＳＴと辺ＳＵはどちらも10㎝です。
三角形STUの体積は、10×10÷2×20＝1000㎤

全体の立体の体積は、
20×10×45＝9000㎤
残りの体積は、9000－1000＝8000㎤

ここまでは、「ふつう」ですよね。「いつも出ているパターン」です。

ただ、しかし！！
いつも、そうかもしれませんが、テストでは、
あえて、違う角度から問題が出されることが多々あります。

どういうことかと言いますと、
次を見てみましょう。

問題２：問題：下の立体には水がいっぱい入っています。この立体をABを床につけたまま、45°傾けたとき、
残った水の体積を求めなさい。

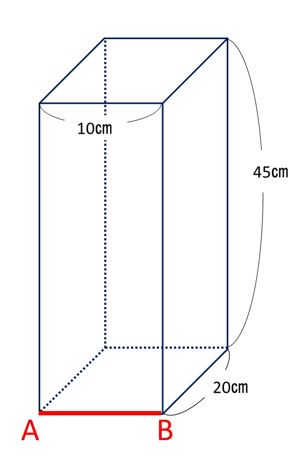
問題は、まったく前述と同じです。

先ほども、申し上げた通り、
問題では、「AB」のラインを赤で描いてくれていないので、
問題をよんでいる子たちは、「AB」を「いつもと同じ」と考えて、
「20cm」のところを軸に考えてしまう生徒が多いのです。

しかし、これは、手前の「10㎝のところ」を「AB」としているので、
傾ける場所がいつもと違うのです。

真横から見た図を描くと、

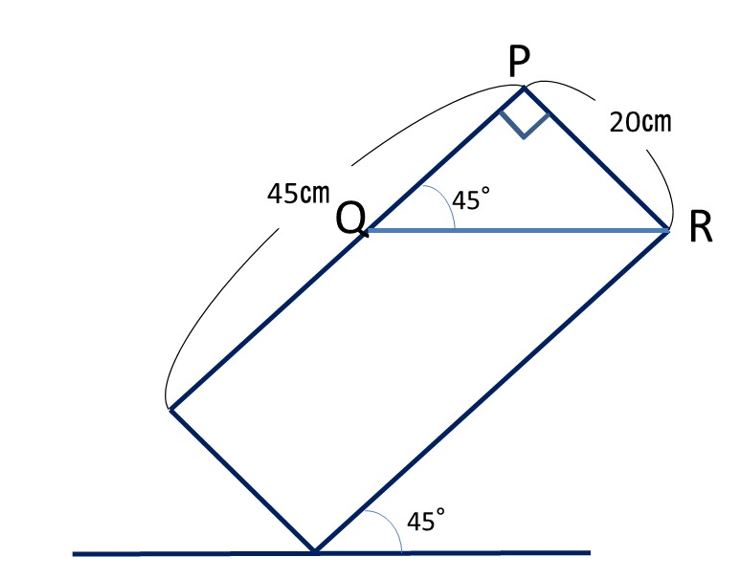
この図は、先ほどの、問題１の解説図とほぼ同じですね。

どこが大きく違うか。
皆さん、お気づきですか？

そうですね、PRの長さが20㎝となっております。
なので、傾けたときにできる図形は、問題１と同じ、直角二等辺三角形です。
しかし、使うべき辺の長さが違うのです。

解説：

三角形PQRは直角二等辺三角形なので、
辺ＰＱと辺ＰＲはどちらも20㎝です。

20×20÷2×10＝2000㎤

全体が9000㎤より、9000－2000＝7000㎤

落ち着いて家で解けばわかったのに～と、いう声をよく聞きます。

ただ、テストで点数をとるには、テストの時間内で、点数となる取り方をしなくてはいけません。

「いつも」と同じ視点からではない問題もたくさん出てきます。
そこに気付けるようになるには、気持ちの余裕が大事なんですが、
余裕をもてるまでには時間がかかります。

その前に、やはり、同じ視点ではない問題があるということも知っておきましょう。
「ふつう」とか「いつもとおなじ」とは限りません。

テストでは、最大限の「集中力」で挑んでほしいと思います。

それでは、本日は、これまでにしておきます。