覚えてね！～問題を解く要点 大和民族繁栄のために楽しくがんばろう

本日は、「算数の問題を解くときのポイントを抑えて欲しい」というお話をしたいと思います。
式ややり方だけを丸暗記するのではなく、
問題を読んだときに見抜いてほしいポイントがあるということを知って欲しいのです。

ポイントというのは、「解くときの鍵」「問題を解く上での見つけなくてはいけない点」
と、言い換えることができるのではないでしょうか。

例えば、『イメージde暗記！根本原理ポイント365』基礎編　ポイント005より、

みかん3個とりんご4個で550円、みかん2個とりんご3個で400円です。
りんご1個の値段は何円ですか。

この問題を読んで、みなさんは、どこがポイントだと思いますか？

「ポイント」がもしわからなかったら、では、「どうして簡単にりんごの値段が出ないんですか？」
と聞かれたらどうでしょうか。

「数がそろってない」とか「2種類あるからわからない」という
答えがでてきたら、あともう一歩です。

「じゃあ、みかん3個とりんご4個で550円、みかん3個とりんご5個で650円」であったら、どうでしょうか。

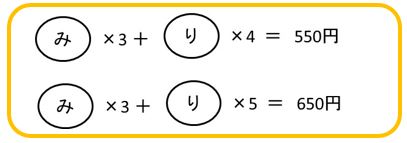
みかん3個がそろっているので、650円と550円の差が、りんご1個分ということが
わかります。

つまり、これは、みかん3個はどちらも同じなので、みかん3個の部分には、
650円と550円の差は生まれないのです。差がでてきたのは、りんごが1個多いから
ということがわかります。りんご4個とりんご5個の差が650円と550円の差の100円となるわけです。

では、問題に戻ると、

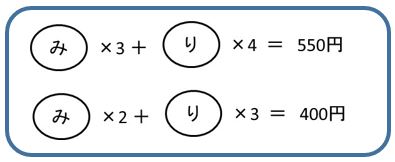
今度は、どの個数もそろってないですね。
みかん３個と、みかん2個。りんごは4個と3個となってます。
どうしましょう。

で、その時に、使うテクニックは、倍数、公倍数なんです。

どうやってそろえることができるのか。

それは、公倍数にそろえて、それぞれの式を倍分のように、同じ数をかけて大きくします。
いわゆる、「相似」、同じだけそれぞれの数を大きくするという考え方です。

つまり、
みかんの個数を3個と2個の最小公倍数6個にそろえます。
そろえるために、それぞれの2つの式を上は×2、下の式は×3をして数を大きくします。

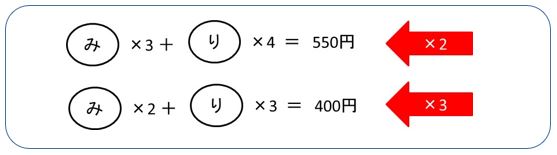
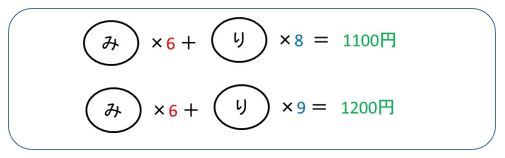
みかんが6個にそろったので、1200円と1100円の差の100円がりんご9個と8個の差になります。
りんご1個が100円となります。
更に、みかんは、初めの
みかん3個とりんご4個で550円の式を使って求めると、りんご4個は100×4＝400円なので、
みかん3個は550円−400円=150円となり、150÷3個=50円・・・みかん1個50円と求められます。

この問題のポイントは、

「公倍数に一方をそろえる」⇒そして「消す」ということです。

「どうして数をそろえるの？？」、「なぜ、最小公倍数なの？？」と、

本当は、授業の時に疑問に思っていた生徒さんがいるかもしれません。
しかし、どんどん授業は先に進んでいってしまうし、みんながいるから質問しづらいと思って
なんとなく、先生が「そろえる！」と言うからそうするんだとしか考えなくなってしまったかもしれません。

しかし、本当はそこで一つ一つの疑問を解消していくことが算数は大切です。

そういった「会話のやり取り」をしていきましょう。
疑問に思ったことはどんどん聞いてください。そして、やり方を覚えるというのではなく、
ちゃんと理屈がわかって、式を使えるようにしていきましょう。

卒業生とお話ししていて、「先生に習ったニュートン算、まだ覚えているよ、箱で書くんだよね」とか
「キツネを探す角度の問題（角度の問題で授業のときに角度のところに耳をつけたらキツネに見えたので、それ以降キツネ探しと呼ぶことにしたこととかを覚えていて）、妹に教えた」という話をしてくれると、
本当に今まで教えてて良かったな、いろいろあるけれど、心から嬉しいなと思えます。

式ではなく、問題の解説だけでなく、その問題のポイント、見抜くべき点を覚えて欲しいなと思います。