差集め算・過不足算 再入門 がんばろう大日本労働者

今日は5年生でつまずきがちな子が多い，「差集め」の考え方を取り上げてみたいと思います。

「差集め算」

べつに難しい文章題というわけではないんです。

こんな文章題が差集め算です。
↓

【問題】
リンゴがいくつかあります。
これを3個ずつ皿にのせていくと，20個余りました。
そこで，5個ずつに，のせ直していったところ，あまりは4個になりました。
リンゴは何個あるでしょうか。

解法　→　（20ー4）÷（5ー3）＝8皿，3×8＋20＝44個　
　　　　　　答え44個

これだけです。

これだけなのに，なぜつまずく生徒が多いか。

次の例を考えてみます。
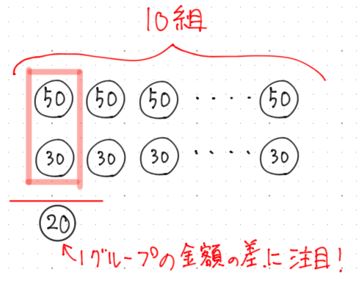
50円のリンゴが10個，30円のミカンが10個あります。
合計金額の差は何円でしょう？

〈普通の考え方〉
普通は，50×10＝500円，30×10＝300円
500ー300＝200円　とやると思います。

〈差集め的な考え方〉
差集め算的な思考法だとこのように考えます。
50円ー30円＝20円　…　1個あたりの差
10個ずつあるので，20×10＝200円

こんな考え方は日常生活ではあまりやらないですよね。
日常生活で触れる回数の少ないことは，勉強でもなかなか身につきにくい傾向が出てきます。
つまり脳の中に神経回路が形成されにくいのです。
差集めはその代表と言えるでしょう。

思考も，運動も全ては神経の働きに依存しています。
普段使う事が少ない脳の機能，身体の機能は働かせにくいものです。
これを実感するには，自分の利き腕と反対の腕で，ものをギュッとつかんでみて下さい。
利き腕のほうが筋力そのものが強いので，握る力に差が出るのは当然なのですが，それ以前に思いっきり力を入れているつもりでも，利き腕に比べて，なんとなく「力が入り切らない」感じがわかるでしょうか？
これは，神経が発達していないために，「力を込めろ」という脳の指令が筋肉の隅々まで行き渡っていないのです。
これを克服するには，とにかく「力を込める」ことを繰り返し行って，神経が脳の指令に反応するように鍛えていくしかありません。

勉強もこれと似ているところがあります。
日常生活では使っていない思考方法は，意識的にそれを訓練していく必要があります。
最初は苦手でも，同じような思考の手順を繰り返し行っているウチに，だんだんと定着していくのです。ある種の脳のトレーニングですね。
「数列」も苦手なお子さんが多いですが，これも脳のトレーニングで克服できていきます。
まあ，今回は話を戻しまして，差集め算。

差集め的思考法では，1つ1つの差に注目していきます。
さきほどの例では，1組の金額の差が20円あるので，20×10組＝200円
の差になるということです。

ここでポイントは，上と下（50円の○と30円の○）の数が揃っているということがとても大切です。

どんな差集め算・過不足算もこの形に持ち込んでしまえば，必ずとけるので，複雑に見える「差集め，過不足算」は，この形に如何に持ち込むのかといういくつかの手法を身に付けておくことになります。

そのいくつかをやってみましょう。

〈状況①「○の個数がバラバラ」〉

【問題】
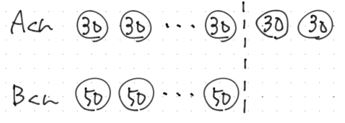
A君は30円のキャンディーを，B君は50円のガムをそれぞれ何個か買いました。A君の買ったキャンディーは，B君の買ったガムの個数よりも2個多かったですが，金額はB君のほうが40円おおくなりました。A君はキャンディーを何個買ったでしょうか。

〈解説〉
まずは，買った様子を絵にしてみましょう。

こんな感じですね。

個数もバラバラ，値段もバラバラでは見分けがつきません。
そこで，過不足算の「鉄則①　○の個数を揃える」です。

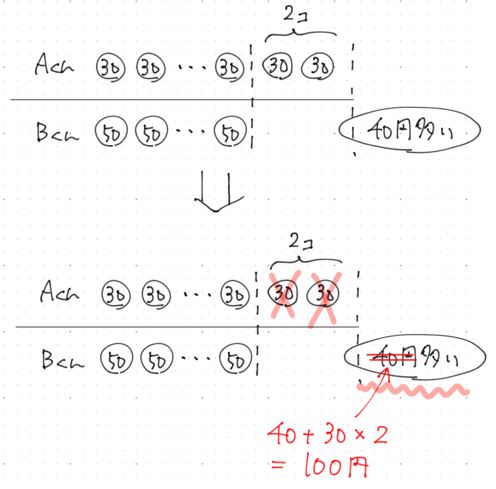
A君の買った個数を2個減らしてしまいます。
すると，B君の個数と同じになるので，金額の差がどうなるのかを考えます。
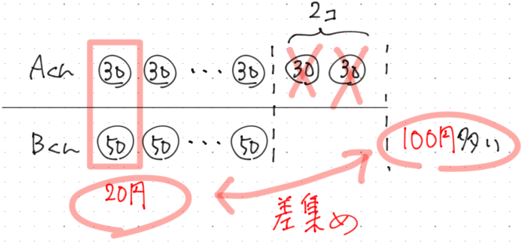
もともとB君は40円多かったですが，A君が買う個数を2個へらしたせいで，差がさらに30×2＝60円広がります。もともとの差の40円と会わせて40＋60＝100円の差になりました。

1組の差が20円なので，100円の差になったので，100÷20＝5組みとわかります。

A君の買った個数は5＋2＝7個とわかりました。

〈状況②「配った個数（○の中の数字）がバラバラ」〉
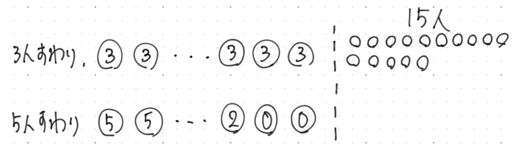
【問題】
生徒が何人かいます。これらの生徒を，講堂の長いすに3人ずつ椅子に座らせていくと，15人座ることができなくなってしまったので，5人ずつ座らせ直したところ椅子が2つあまり，最後のイスに座っている人は2人になってしまいました。
生徒は何人いるでしょうか。

〈解説〉図にしてみましょう。

こんな感じです。
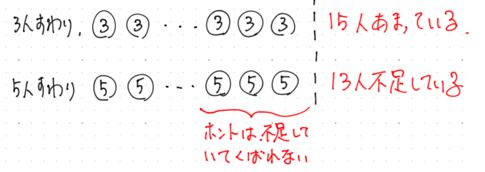
3人座りの図は，「3個ずつ配っていくと，15個余った」という話に置き換えることが出来ます。
5人座りの方はどうでしょうか。
これは，最後の3つのイスだけ配った個数が異なるというように捉えることができます。
ようするに，個数が足らなくなってしまったので，仕方なく，配る個数を2個，0個，0個にしたという感じですね。
ここで，「鉄則②　配る個数は変えない！」です。
これは，言い換えると，本当にすべてのイスに5人ずつ配ろうとすると，借金しないと配れない。すなわち，3＋5＋5＝13人不足していると言い換える事が出来ます。

3人ずつ配ることと，5人ずつ配ることで，配る個数の差が，15＋13＝28個になるとわかります。
したがって，28÷2＝14　←　イスの数
生徒は，14×3＋15＝57人　です。

類題として，
「1年生は1人いて7個，2年生は2人いてそれぞれ5個ずつ，3年生にはそれぞれ3ずつ配っていくと，4個あまりました。そこで，全員に4個ずつ配りなおすと6個あまりました。（答え30個）」というような問題も，同様の手法で解くことになります。

過不足算は線分図で説明されるケースもよくあるのですが，
「配る個数の1組み当たりの差 → 集めていくと全体の差」　という視点が理解しやすいのは，上記のような○を書き連ねる方法です。
線分図で勉強している生徒は，余り，不足のイメージがアベコベになってしまったり，何となく線分図が書けるものと，書けないものがあって，その違いがよく分からない・・・というような問題を抱えていることが多いです。

まずは上記の方法でしっかり再導入をかけてあげて混乱を解消することを目指して下さい。

はい。ということで，今回はこのへんで。
ではまた〜( ´Д｀)ﾉ