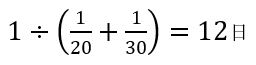仕事算、あなたは①派、最小公倍数派 お父さんは家長で大黒柱

今日のお題は仕事算です。

後期の５年生では、割合も一通り習い終わって、割合を当たり前のように使いこなすことが求められてきますね。

仕事算，実は割合の単元だとちゃんと認識していますか？

仕事算というと，「仕事全体を1とおいて考える」と習ったことを思い出す人も多いでしょう。
実はこの1と考えるという操作が，割合の考え方です。

「Ａくんはあるしごとを完成させるのに20日かかります。Ｂくん同じ仕事を完成させるのに30日かかります。ＡとＢで協力して仕事をすると何日で終わるでしょう」

こんな問題が仕事算ですね。
解き方としては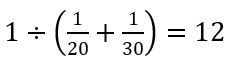，　答え12日　ということになるわけですが，
考えてみたら，こんな理不尽な問題はありません。
仕事といってもいろんな仕事がありますし，それが毎日同じ仕事だとも限りません。
また，仕事は二人で協力したら，単純に効率があがるようなものかどうかだって分かりません。ＡくんがやっていたらＢくんはその仕事が出来ないかもしれない。

リアルな日常生活の感覚を前提にこの問題を考えたら，こんなわけの分からない問題もないだろうなと思います。
（今，自分がその昔小学生の時代に，この問題を目にした時の気持ちを思い出しながら書いています^^:）
算数としての「常識・前提」を共有していない人がいきなりコレを解くことはやっぱり出来ないと思います。

この問題を解く前提になっているのは，
①　仕事は数量化できる。
②　ＡくんもＢくんも毎日一定の量の仕事をする。（たとえば，封筒を100枚作るのに，毎日5枚ずつ作っているとか。）
③　二人で仕事を行うとは，出来上がるものが単純にＡとＢを足した数になる。

ということです。
ここまで，前提を共有すれば，算数を習ったことが無い人でも分かるんじゃないでしょうか。
①数量化できるということは，勝手に仕事の量を数値で決めてしまえば良いわけです。一番手っ取り早いのは，割合を使って仕事全体を1とおくことでしょう。他には100とか，1000とか，適当に好きな数字に決めるのもありですね。

②　勝手に決めていいとは言いましたが，数によっては計算がやりづくらくなるものもあります。全体を100とおくのは，得策ではありません。なぜなら，Ｂ君は30日でこの仕事を完成させるとあるので，100と決めてしまうと，100÷30で割り切れなくなってしまうからです。
ここは，全体の量は，Ａの日数でもＢの日数でも割り切れる量の方がいいですね。なので，60とかがよいでしょう。

③　自分で決めた仕事の量に従って，ＡとＢの1日でやる仕事の量を求めます。
1と決めた人は，Ａは1日に，Ｂは1日にをやることになります。
60と決めた人は，Ａは1日に60÷20＝3，Ｂは60÷30＝2　となります。

協力してやると，仕事の量が和になるので，

60と決めた人の場合は，60÷（2＋3）＝12日　です。

さて，タイトル①派か，最終公倍数派かという問いかけ。
子供達の間では，①派と最小公倍数派で結構相容れない溝があるんですが，
実はあまり重要なポイントではないです。

要するに，仕事の量は決まってないから，自分で決めましょう。それはどうせ割合だからどんな数字に決めても大丈夫ですよ。っていうことがちゃんと分かっていればいいのです。

ちなみに私は、どっち派かというと、どっち派でもありません。
問題の流れをみて、①にするか、最小公倍数にするか使い分けます。

ということで、お話はお終いなのですが、
もうすこしお付き合い下さい。

ここで、「ある量を決まった数量ずつ進めて行く」という点において、関連の深い考え方は何か、わかりますか？

そう。「速さ」の問題ですね。

・道のり（全体量）
・単位時間（1時間、1日など）に進む量
・かかる時間

という3つの要素が、
仕事算では、
・仕事の量（全体量）
・単位時間に終わらせる仕事の量
・かかる時間
に対応しています。

仕事算では仕事が具体的にどれだけあるかなどは、問題では触れられないことが多いため、割合の①で置くわけですが、速さの問題でも、距離を①とおいて考える、仕事算タイプのものもあります。
つまり、仕事算と速さの問題は、まったく同じ解法をとるジャンルと言えます。
違いをあげるとしたら、仕事算は、「協力して進める」「仕事を邪魔する」ことができるという点です。
速さではこういうことはできません。A車とB車が同時にスタートしたら、車のスピードがアップするなんておかしな話になってしまいますから。
算数の文章題は、様々な抽象的な概念を考えさせたいという目的があって、じゃあそれを小学生にどういう風に取り組ませるか？ということを考えた結果、日常生活に無理のない範囲で当てはめられる事象を選んで問題を作っているわけです。
なので、抽象概念ありきでスタートしているので、冒頭の仕事算のようなリアルには有り得ないような問題設定が出てきしまうわけですね。

はい。またまた理屈っぽくなってしまいましたが、
仕事算と速さ。この共通点を認識することは、他の似たような文章題である、ニュートン算、流水算などでも非常に重要なポイントです。
算数の学習でつまずかないためには、特に速さ、割合の概念を深く、丁寧に理解しておくことが重要なのです。

ということで、今回はこのへんでお終い。
ではまた～。(´∀｀*)ﾉ