年齢算 中学受験算数 中学算数 令和

「年齢算」の解き方とポイント｜数直線を使った分かりやすい解法

 

1.  
2.  
3.  
4.  
5.  

 

 

中学受験でしばしば出題される問題のひとつ「年齢算」について解説していきます。

前回は「倍数算」の解説をしましたが、年齢算はこれの一種で解き方はほぼ同じです。この機会にどちらも抑えておきましょう。

いずれにしても問題のパターンはだいたい決まっているので、解き方に慣れるのが大事です。

 

目次 [非表示]

• 年齢算とは
• 年齢算の解き方
  • 例題1
  • 例題2

年齢算とは

年齢算とは複数人の年齢の関係に関する問題。特に親子など2人の年齢の比率が年を経てどのように変化するかが問われることが多いです。

具体的には以下のような問題。

年齢算の例題1
今年の母親の年齢は子の3倍だが14年前は7倍だった。今年の母の年齢を求めよ。

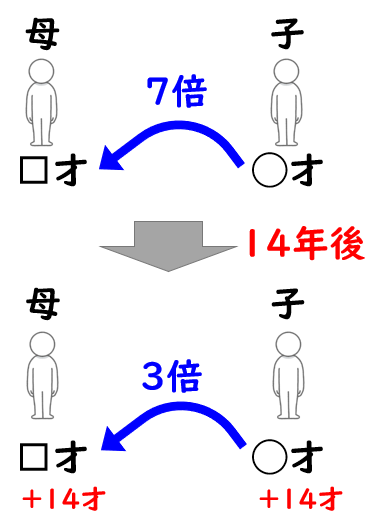
同じように年を取るので、ふたりの年の差が常に一定なのがポイント。

他には異なる人数の年齢の和を考えさせる問題もあります。

年齢算の例題2
両親の年齢の和は子ども3人の年齢の和の7倍で、15年後には2倍になる。現在の子ども3人の年齢の和を求めよ。

年の差が一定ではないので解き方が異なります。

ではそれぞれの年齢算の解き方について詳しく見ていきましょう。

年齢算の解き方

例題1

年齢算の例題1
今年の親の年齢は子の3倍だが14年前は7倍だった。今年の母の年齢を求めよ。

14年前の親と子の年齢を数直線で表します。親と子の年齢の差が常に一定というのが重要なので、両者の差がわかりやすいように数直線を書くのがポイント。

子を「1」とすると親の年齢は「7」にあたり、子と親の年齢の差は「6」です。

「それぞれの年齢に14才を足したら親は子の3倍の年齢になる」という情報を加えましょう。このときの子の年齢を「1」とすると親の年齢は「3」なので親子の年齢差は「2」にあたります。

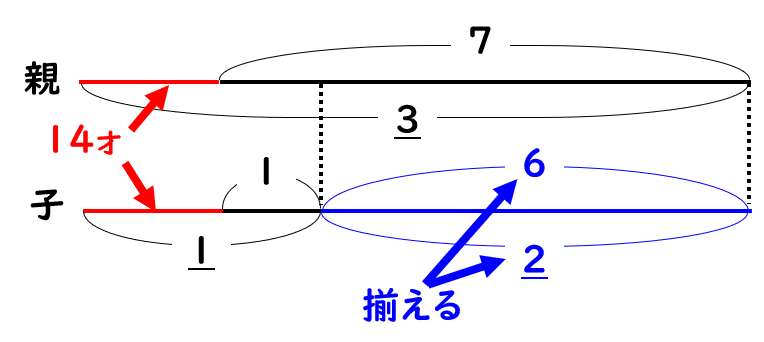
これで問題文の情報をすべて数直線で表すことができました。

しかしこのままだと数直線の上下で比の割合が異なります。値が同じである「親子の年齢差」の比を揃えることで比の割合を揃えましょう。

14年後の親子の年齢差の比を「2」から「6」にするために、比を3倍にします。⇒「3：1＝9：3」

こうすることで上下の比の割合が揃うので、14才がこの比の「2」にあたるというのが分かります。

この比の「1」にあたるのは、14÷2＝7より、7才です。

問われている現在の親の年齢を計算しましょう。現在の親の年齢はこの比の「9」にあたるため、9×7＝63より63才が答えです。

一応、これが問題文に合致しているか確認しましょう。

現在の子の年齢は親の1313なので21才。14年前はそれぞれ49才と7才となるため7倍になっているのが確認できました。

さてこの問題のポイントは、常に一定の数値である「年齢の差」に着目し、この比を揃えるということです。

倍数算のときにも述べましたが、「1」にあたる数値が異なる複数の比が出てきた時、同じ数値にあたる比を揃えることで「1」にあたる数値も揃えることができるのです。

複数の比が出てくる場合、同じ数値の比を揃える

例題2

両親の年齢の和は子ども3人の年齢の和の7倍で、15年後には2倍になる。現在の子ども3人の年齢の和を求めよ。

まず両親と子ども3人のそれぞれの年齢の和を数直線で表します。

「15年経ったら両親の年齢の和が子どもの年齢の和の2倍になる」という情報を追加します。両親は2人なので15年で30才、子どもは3人なので15年で45才増えます。

前の問題とは異なり年の差は一定ではないので比を揃えることができません。ここでは数直線の長さを揃えましょう。

15年後の子ども3人の年齢の和を2倍すると両親の年齢の和と同じになります。これを数直線で表すと以下の通り。

この数直線から問題をこのように変換することができます。

『両親と子ども3人の年齢の比は7：2、両親の年齢の和に30足して子どもの年齢の和に90を足したら同じ年齢になる』

数直線からわかると思いますが、このときの比の差の「5」（＝7-2）が足した年齢の差60才に当たります。

つまりこの比の「1」は60÷5＝12より12才です。現在の子ども3人の年齢の和はこの比の「1」にあたるので、答えは12才です。

一応これが問題文に合致しているか確認しましょう。

現在の両親の年齢の和は子どもの7倍なので84才。15年経つと子どもの年齢の和は+45才で57才、両親の年齢の和は+30才で114才。

両親の年齢の和は子供の年齢の和の2倍になっているのが分かりますね。

 

倍数算でもこの種の問題について解説しましたが、一定の数量がなく比が揃えられない場合、実際の数量を揃えるのがポイントです。

比率が揃えられない場合は実際の数量（数直線の長さ）を揃える

年齢算はスムーズに特には慣れが必要なので、問題をこなすのが重要です。

倍数算と共通するポイントが多いので合わせて抑えておくのをおすすめします。

ちなみに年齢算について、自由に印刷できる練習問題を用意しました。数値はランダムで変わり無数に問題を作ることができるので、ぜひ