
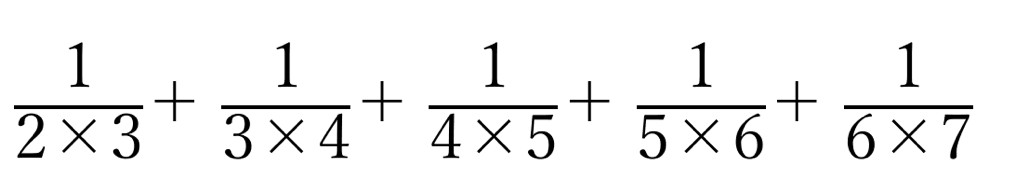
こんな計算問題を…
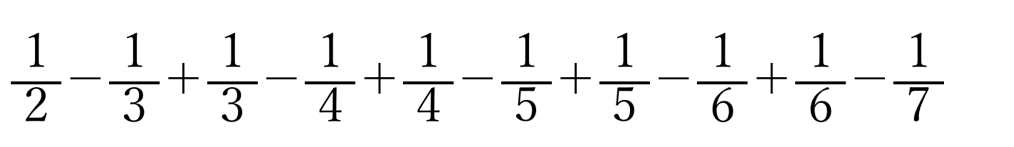
こんな風に変形して…

途中の分数を打ち消すことで、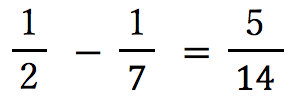 と計算できることを確認しました。
と計算できることを確認しました。
その際、
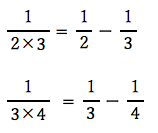
などのように分数の差に変形できることを、
さて今回は、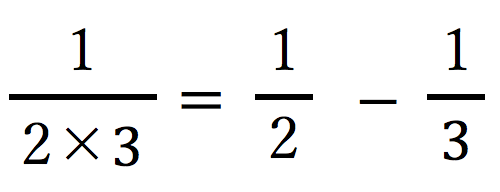 や、
や、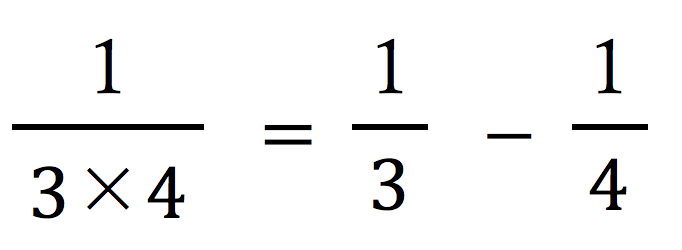 などの部分について、
などの部分について、
突然ですが、
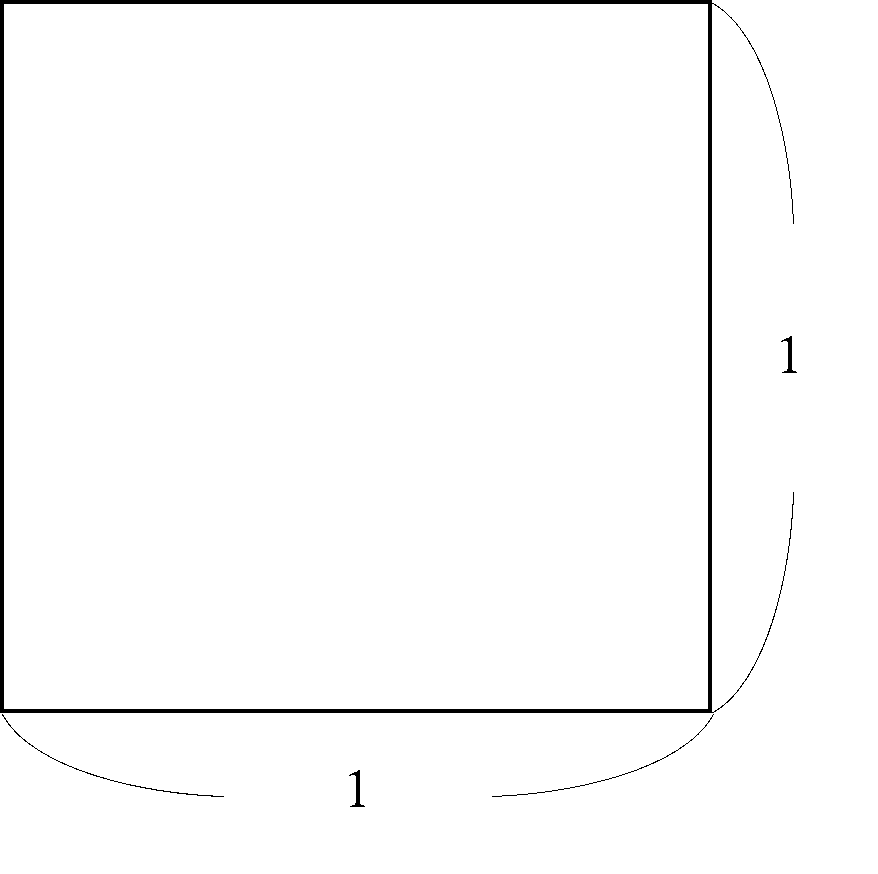
1辺の長さが1の正方形を考えてみましょう。
この正方形の縦の辺を2等分、横の辺を3等分します。
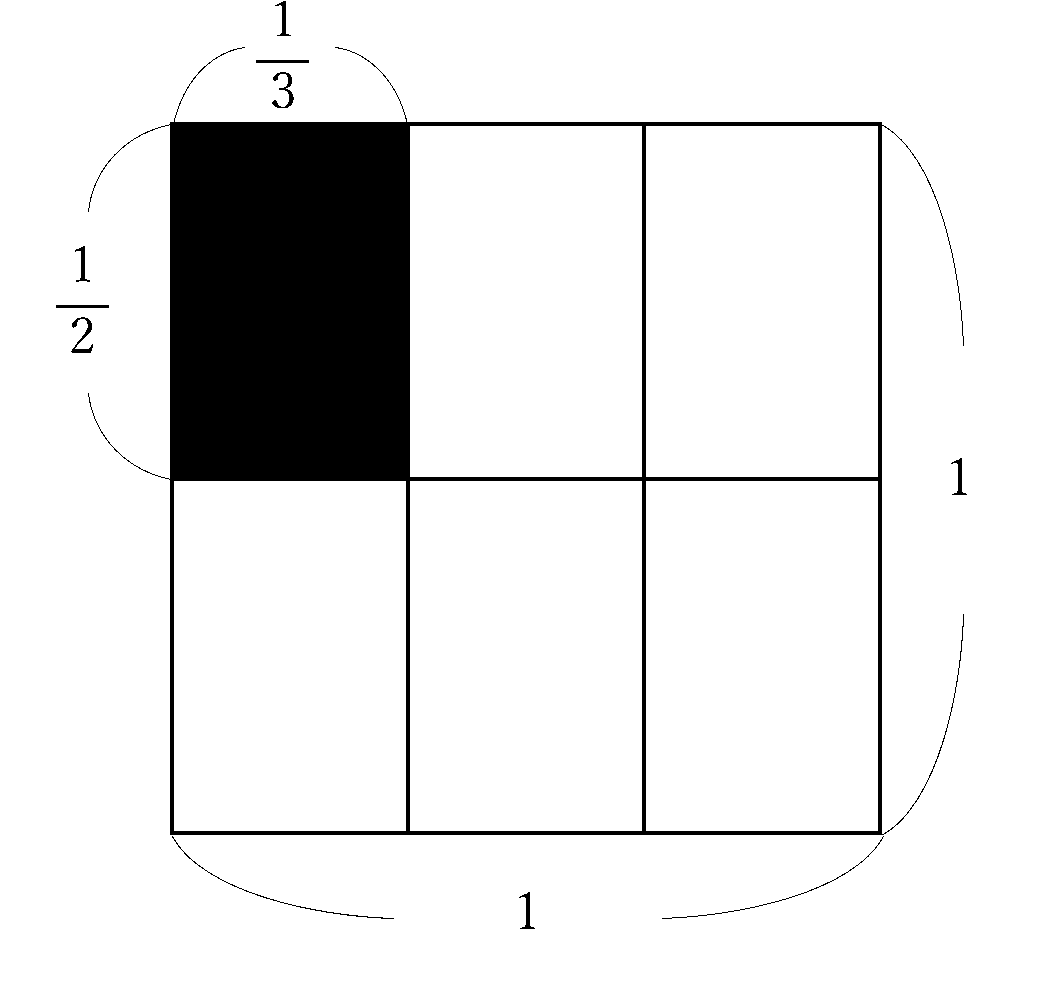
こんな図になりました。小さい灰色の長方形1個分で、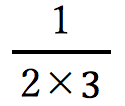 を表してい
を表してい
そして…

このように横長の長方形を考えると、これは![]() を表していて、
を表していて、
また、

この青い縦長の長方形は、![]() を表していて、
を表していて、
ということは、小さい長方形の個数に注目すると、1=3-

確かに、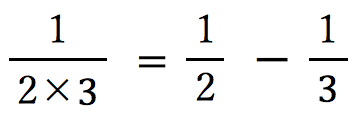 の式が成り立っています。
の式が成り立っています。
こんな形で、式を図形的にとらえることができました!
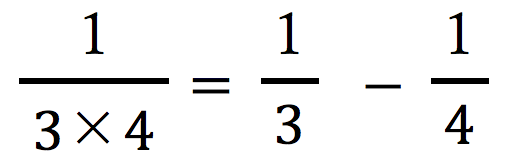 や、
や、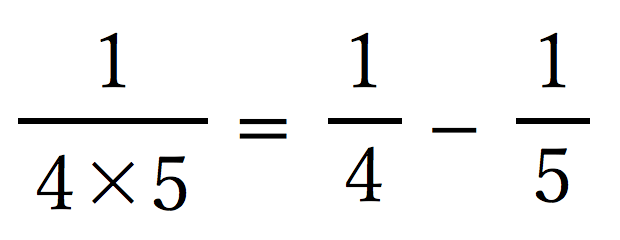 も同様に、
も同様に、

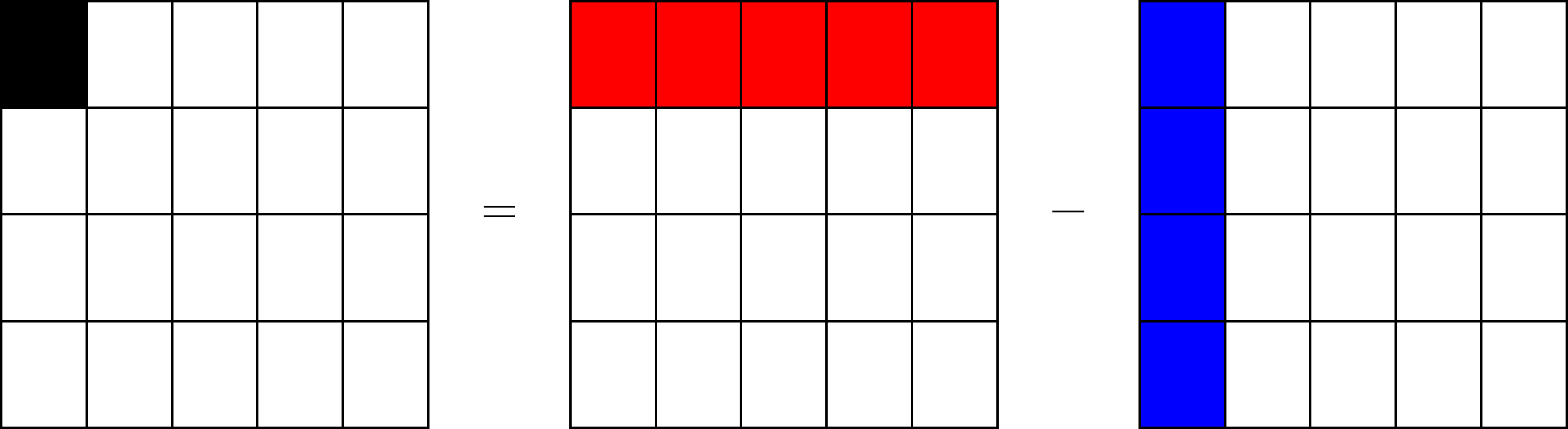
このような図で表せています。それぞれ、
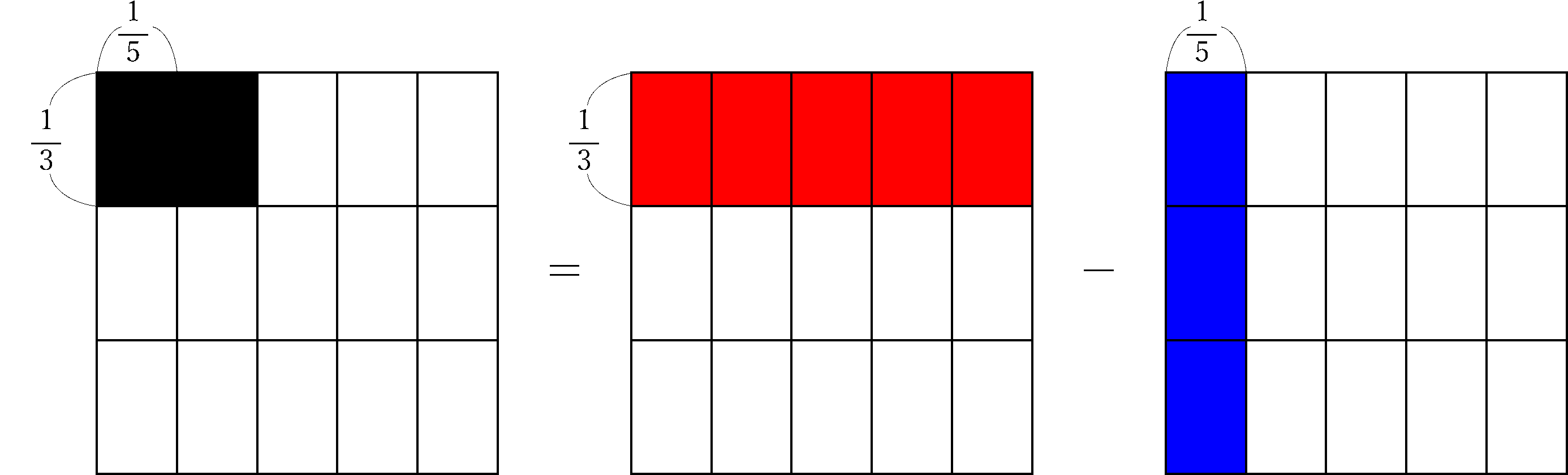
今度は、![]() について考えてみましょう。縦を3等分、
について考えてみましょう。縦を3等分、
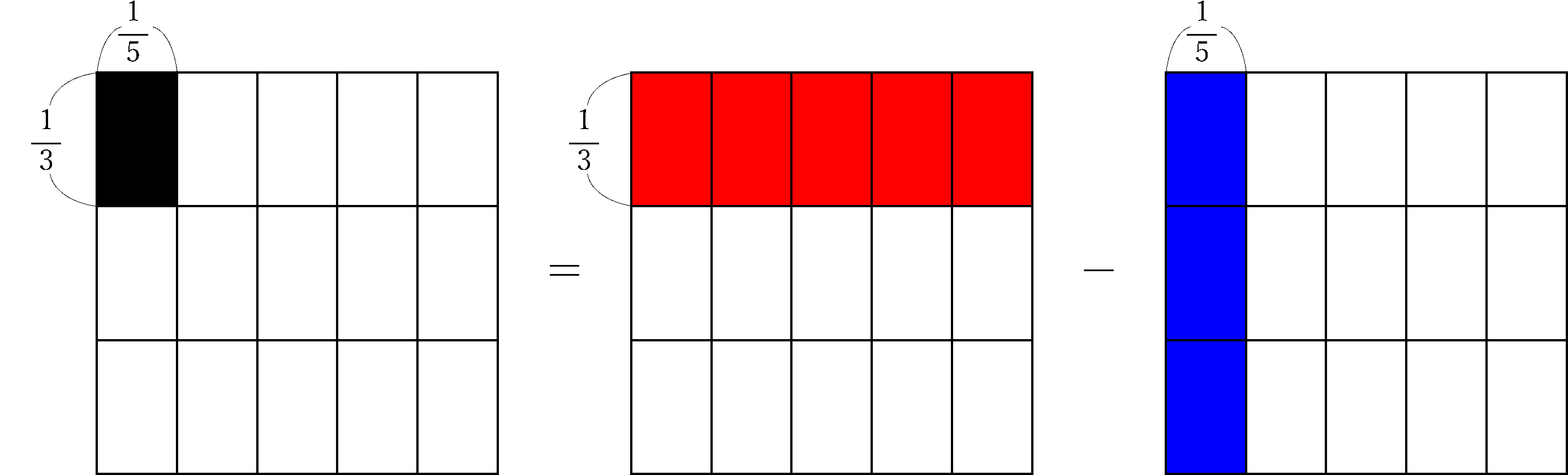
これまでと同じように、上のような図で考えれば…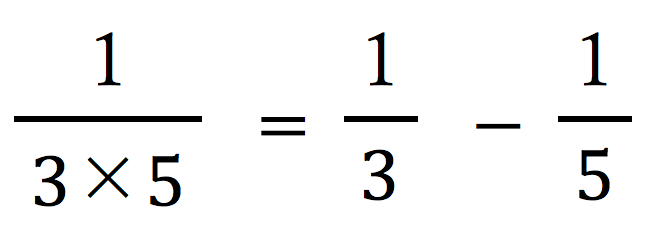
…
…
…
では、ありませんね!![]() を表している赤い長方形は小さい長方形5つ分、
を表している赤い長方形は小さい長方形5つ分、![]() を表している青い
を表している青い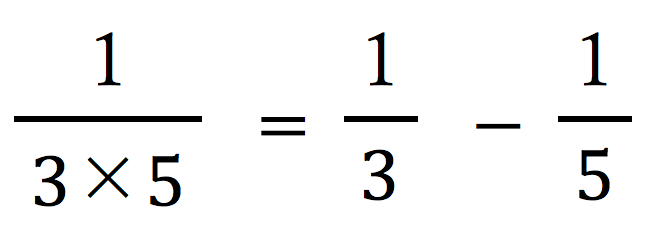
ではなく、
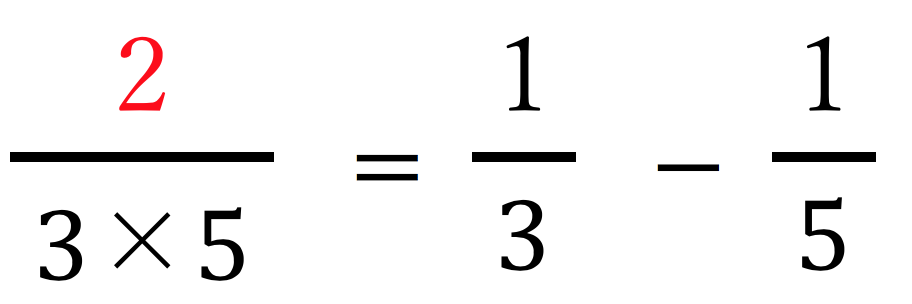
が正しいのです。
このように、分母同士の差が1になっている、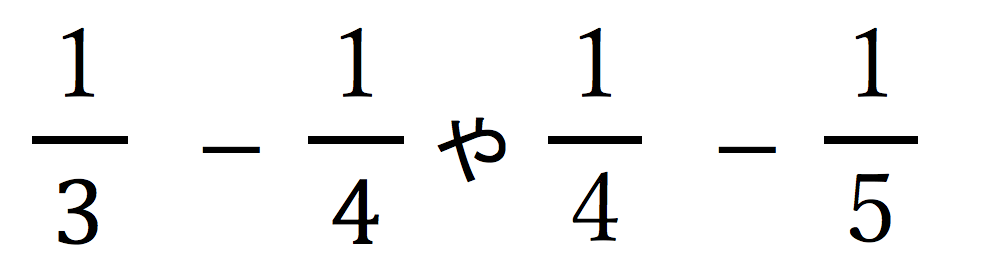 などとは様子が違っ
などとは様子が違っ
では、少しひねられたキセル算、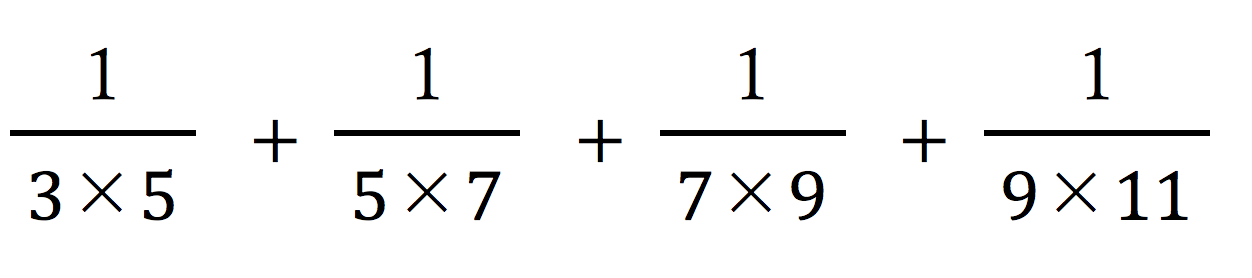
のような問題は、どう計算したら良いのでしょう?
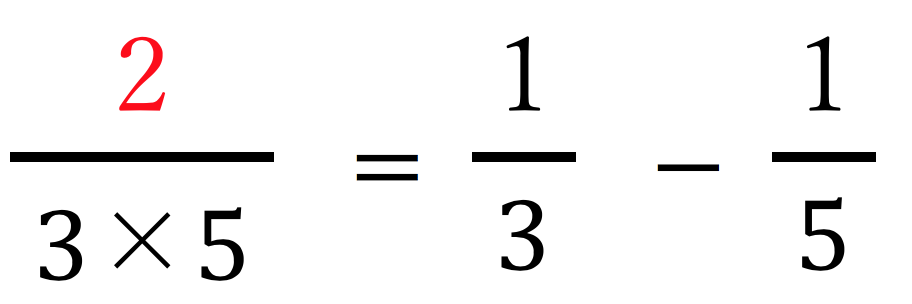
が正しいということは、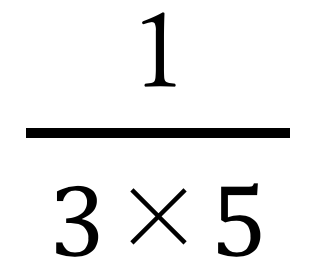 は、この値の半分。つまり、
は、この値の半分。つまり、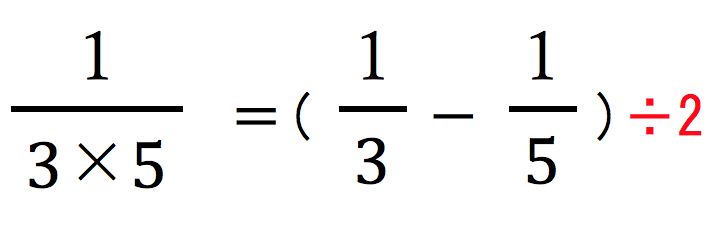 と表せます。
と表せます。
同じように、
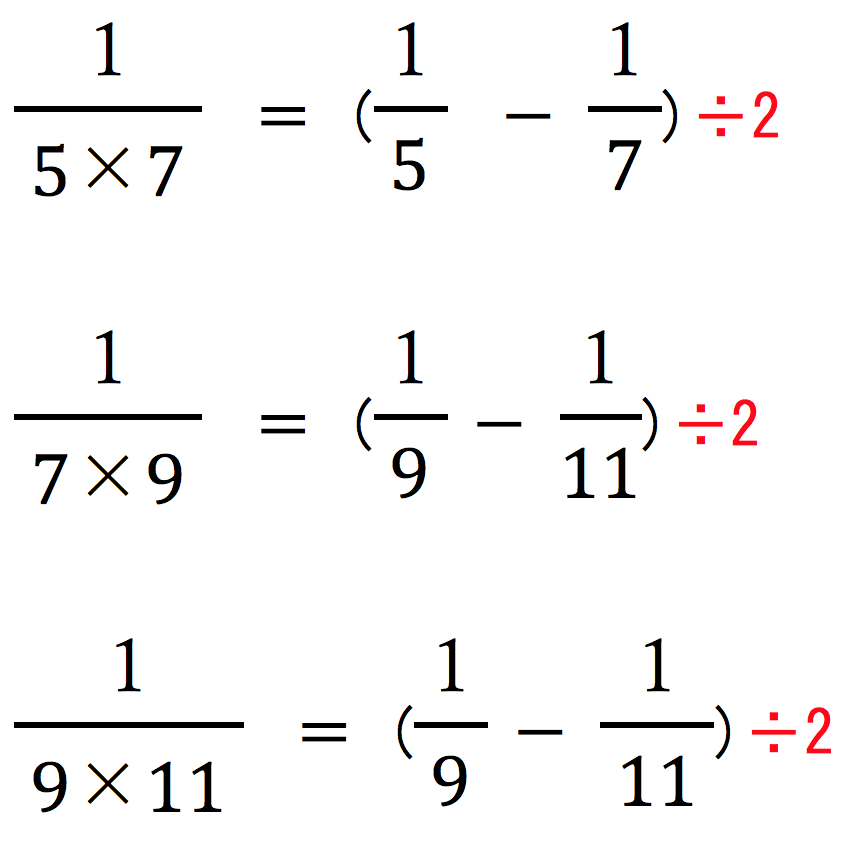
と変形できるので、
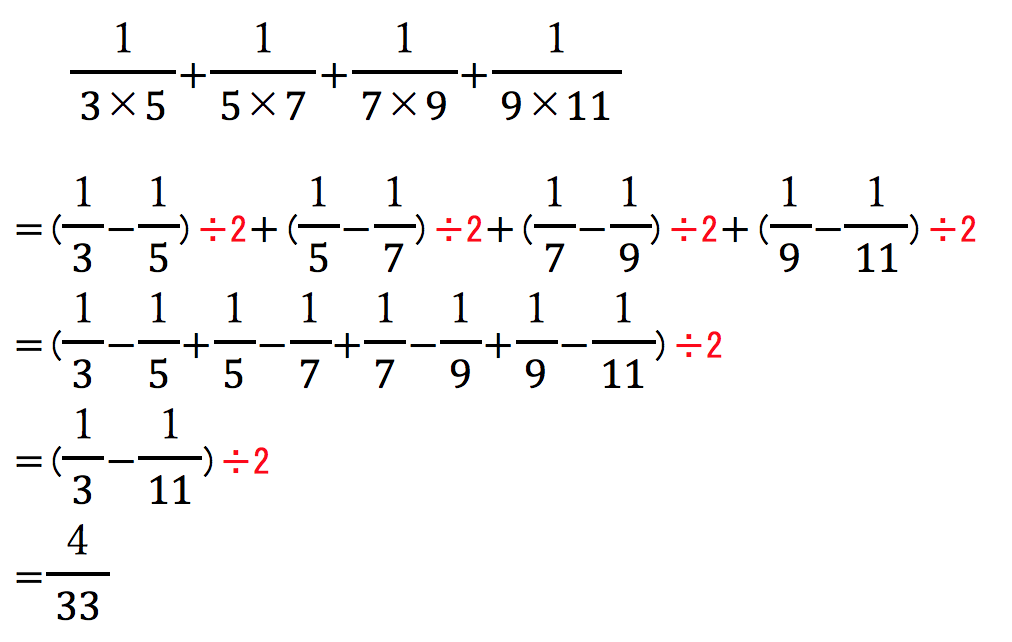
と、無事に計算できました!
キセル算では、計算のしくみや理由をきちんと理解しないままに、
ひねられてもきちんと対応できるように、
今回は、ここまで!















