【N進法】ホテルの部屋番号問題の解き方 令和大日本がんばろう

 

N進法を使う問題で、ホテルの部屋番号に関する問題をご紹介します。

例題1：あるホテルには、1号室から85号室まであります。
ただし、部屋番号に「4」と「9」の数字は使っていません。
例えば、1号室、2号室、3号室の次は5号室になります。8号室の次は10号室です。38号室の次は50号室になります。
このホテルには何部屋あるでしょうか？

このような問題です。
これは「4」と「9」という2種類の数字を使っていないので、八進法という考え方を使って解いていきます。
しかしこのまま解説しても面白くありませんので、もう一問例題を考えて、その後でこの問題に戻ってきたいと思います。

例題2：ドクター星のドクター星人からメッセージが届きました。ドクター星では地球のような十進法ではなく、八進法で数を数えていました。
使っている数字も地球のようなアラビア数字ではなく、ドクター星独自の数字を使っています。
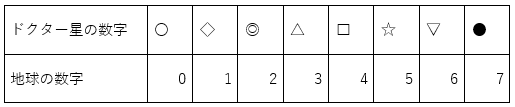
ドクター星の数字と地球の数字の翻訳表は以下の通りです。

 

ドクター星人から次のようなメッセージが届きました。
「◎☆□」
これは地球で使われている十進法に翻訳すると、いくつになるでしょうか？

この問題を考えていきましょう。
決して遊びではなく、冒頭の部屋番号の問題を解くためのステップとなる問題です。

まずは、宇宙語を翻訳するところから始めましょう。
宇宙語の「◎☆□」は地球の数字に置き換えると「254」となります。

次に、八進法から十進法に変換する作業をします。
今はまだ宇宙語から地球の数字に翻訳した段階ですので、この「254」は八進法の254です。
64×2+8×5+1×4＝172
が答えです。

解法の流れをおさらいすると
①宇宙数字を地球数字に置き換える
②八進法を十進法に置き換える

という２段階で解いています。

では、冒頭の例題1に戻るのですが、もう少しだけ寄り道をします。
例題1の文章表現だけ少し変えた問題を出題します。

例題3：ホテル星のホテル星人からメッセージが届きました。ホテル星では地球のような十進法ではなく、「4」と「9」以外の8種類の数字を使って、八進法で数を数えていました。
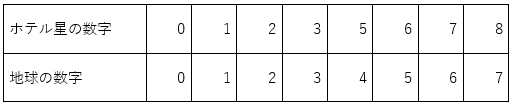
つまり下の表のように数字を使っていました。

 

ホテル星人から次のようなメッセージが届きました。
「85」
これは地球で使われている十進法に翻訳すると、いくつになるでしょうか？

このように表現を変えたらどうでしょうか？
先ほどのドクター星人の場合と同様の手順で解いていきましょう。

つまり、

ホテル数字の八進法→地球数字の八進法→地球数字の十進法

という2段階で置き換えていきます。

ホテル数字の「85」は上の表に従って地球数字に置き換えると「8→7」「5→4」ですので74になります。
これは八進法ですので、十進法に置き換えます。
8×7+1×4＝60
より、ホテル星人からのメッセージである「85」は私たちが普段使っている十進法に置き換えると60であることが分かりました。

さてお待たせしました。冒頭の例題1を再掲します。

例題1：あるホテルには、001号室から85号室まであります。
ただし、部屋番号に「4」と「9」の数字は使っていません。
例えば、1号室、2号室、3号室の次は5号室になります。8号室の次は10号室です。38号室の次は50号室になります。
このホテルには何部屋あるでしょうか？

この問題が、例題3のホテル星人の問題と同じだ！　と気づければもう大丈夫です。
生徒は自力で答えを出すことができますので、解説はここまでです。

まとめます。

「～と～の数字を使わない」という問題は、特殊なN進法です。今回のホテル問題の場合は特殊な八進法でした。

ここから二段階で変換します。

特殊なN進法→普通のN進法→十進法

の順番で置き換えます。

この根本原理が分かれば、もう怖くありません！
一見難しそうな問題も分解できれば攻略できます。

令和二年十月