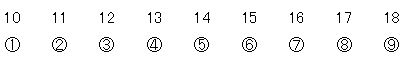先日、土偶に会いに行きました。
上野は国立博物館。
入場券は620円。
右手の東洋館には目もくれず、
土偶のいる本館に突撃。
広いですねぇ。
1Fと2F。
時代ごとに展示されています。
縄文時代の土器、
弥生時代の銅鐸、
古墳時代の埴輪、
飛鳥時代の仏像、
あれ、土偶は?
ないぞぉ。
「すみません。土偶はないんでしょうか…」
「本館ではなく、平成館にて展示しております」
なんと!
さすが土偶。
なかなか会えませんね。
いそいそと平成館に向かいます。
いました!ごたいめ~ん♪
実際にみた遮光器土偶は左脚部分が欠けていましたが。
縄文時代は、
紀元前14000年ごろから紀元前300年ごろまでとか。
14000 - 300 = 13700年間
長いですねぇ。
13700年間も縄文時代だったとはねぇ。
ちょっと待っったぁぁぁぁ~~~
13701年間ですよ!
へっ、どゆこと??
そこよく引っかかるんですよ。
算数でよくある間違い。
土偶と学ぶ数の個数。
では、いってみよー。
マジで?8じゃないの?
1から8までは何個の整数がありますか?
8個だよ!
当たり前ジャン。
数えてみましょう。
1 2 3 4 5 6 7 8
うん。8個ですね。
では次の問題。
10から18までは何個の整数がありますか?
8個だよ!
当たり前ジャン。
数えてみましょう。
はい、9個。
えっ?9個?
18 - 10 = 8
8個じゃないの?
でも9個だよなぁ。
ではここで土偶に登場してもらいましょう。
土偶と学ぶ
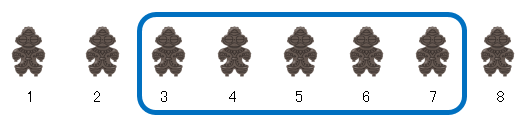
土偶が8個並んでいますね。
3番目の土偶から、7番目の土偶まで、
土偶は何個ありますか?
7 - 3 = 4
4個!
いや、それがダメなんだって。
3番目から7番目までを、青い枠で囲ってみましょう。
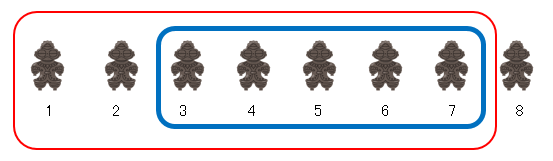
さらに、
1番目から7番目までを、赤い枠で囲ってみましょう。
赤い枠内に、土偶は何個ありますか?
1番目から7番目だから、、、7個。
青い枠内の土偶は、7個から2個引いて、
7 – 2 = 5
5個!
そうです。
3番目から7番目の土偶の個数は、
7 – 3 = 4
ではなく、
7 – 2 = 5
が正解なんですね。
じゃあなんで、
1から8までの整数の個数のときは、
8個でよかったのか。
それはね、
8 - 0 = 8
1からと言われたら、
自然と0を引いているので、
8個になったんです。
縄文式算数
もう大丈夫ですね。
100から500まで整数は何個ありますか?
という問題なら、
500 - 99=401
401個。
紀元前14000年から紀元前300年なら、
14000 - 299 = 13701
13701年間。
これぞ縄文式算数!
インド式には負けん。
気分はもう土偶ですね。
縄文時代サイコー!
今宵はここまで。
ではまた。