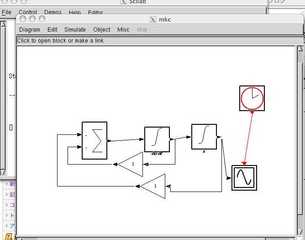
なんとか,MATLABでのSimlinkの機能がscicos()←関数としてScilabのウインドで走る
前回の運動方程式を変形してみて
d2/dt2 X= -K/M*X-C/M*dX/dt
となるから
加速度は積分して速度
速度は積分して位置へ
それらに係数を掛けて
足したのが加速度
という関係を表せばシミュレションは簡単にできる
図で 時計のマークはMATLABにはない
時間のシミュレションをするためのカウンタの役割と考えて良い
ともかく,グラフィカルにシミュレーションできる
目出たい
シミュレーションが合っているかどうかためしてみよう
三角印のゲインはそれぞれ K/M, C/Mを示すから
前回の値としては
k/M=2000000/1000000=2
C=0なので 0
として,初期値
つまりばねを引っ張って放すというシミュレーションができる
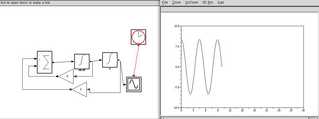
パラメータとして 初期値X=10として,10秒間の現象がシミュレートできた
C=0だから減衰はしない
この系の固有振動数は前回0.225Hzであった
10秒間には2.25回の波となるはずであり,グラフもそうなった
工学では,このようなチェックが重要である 大まかに現象がこうなるという見込みをつける
そうしないと,とんでもない間違いがあっても計算機が計算したから間違いない
などという思い込みをしてしまう
必ず,結果は疑ってみて,結果が妥当かどうか確認する癖をつけたいものだ
今回はここまで
でも,scicosがあれば有料のmatlab,simlinkも必要なくなるのか?
前回の運動方程式を変形してみて
d2/dt2 X= -K/M*X-C/M*dX/dt
となるから
加速度は積分して速度
速度は積分して位置へ
それらに係数を掛けて
足したのが加速度
という関係を表せばシミュレションは簡単にできる
図で 時計のマークはMATLABにはない
時間のシミュレションをするためのカウンタの役割と考えて良い
ともかく,グラフィカルにシミュレーションできる
目出たい
シミュレーションが合っているかどうかためしてみよう
三角印のゲインはそれぞれ K/M, C/Mを示すから
前回の値としては
k/M=2000000/1000000=2
C=0なので 0
として,初期値
つまりばねを引っ張って放すというシミュレーションができる

パラメータとして 初期値X=10として,10秒間の現象がシミュレートできた
C=0だから減衰はしない
この系の固有振動数は前回0.225Hzであった
10秒間には2.25回の波となるはずであり,グラフもそうなった
工学では,このようなチェックが重要である 大まかに現象がこうなるという見込みをつける
そうしないと,とんでもない間違いがあっても計算機が計算したから間違いない
などという思い込みをしてしまう
必ず,結果は疑ってみて,結果が妥当かどうか確認する癖をつけたいものだ
今回はここまで
でも,scicosがあれば有料のmatlab,simlinkも必要なくなるのか?