モデルの作成についてから続きである
シミュレーションの実行にあたって,モデリングがうまく行けば,80%から90%はその仕事が終わったと言って良い.非線形である場合には,解析手法の調整が大変であったりするが,モデルが出来ればそこからは早いのが一般的である.まあ,報告書などをまとめるというのに時間がかかるが,それは別としてである.
簡単な例題からScilabに試させてみよう
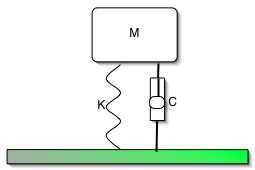
図のような一自由度系の簡単な振動系を考える.
数学モデルであるから
上下方向の自由度を表す変数をxとして
Md2x/dt2+Kx+Cdx/dt=0 ....(1)
となる d2x/dt2はxの2回微分 dx/dtは一回微分で,それぞれ加速度,速度を表すことは言うまでもない
モデルとしてxの運動を記述できたわけである.MATLABであればsimlinkを使って積分していけばxの値を計算してグラフに表すのは簡単である.さて,scilabにはどんかToolBoxがあるのか
まずここらへんを調べておかなければならない.
であるが今回は
その前に,基本的な特性がわかるかどうかやってみる
(1)式は,線形の振動方程式であり,その解x=...というのが
解析的に求まる.振動であるから固有振動数があり
それは ω=√K/M (rad/s)であることはわかっている
例えば M=1,000,000kg(=1000ton)とし,k=2000000(N/m)とすると

というようにscilabで計算できる(あたりまえ)
sqrtが√計算で%piがπを表す
ラジアン/sからHzに直しているわけである
私の扱っている機械が1000tくらいあり,それの固有振動数が,0.22Hzくらいであれば逆にこの程度のばね(剛性)をもっているということがわかる
方程式の解がわかっていたのでこんな計算で対象の振動系の特性=固有振動数を調べることができるのであるが,もうすこしシステムとして考えるとどうすれば良いのであろうか
先ほどのToolBoxを使うというのも手であるが(ToolBoxがあるかどうか,これから調べる),数値シミュレーションであれば,方程式が書ければ,それを一次方程式にしてみるということにより一般的になる場合がある.
そこで X=[x,dx/dt]Tというようにベクトルとして位置x,速度dx/dtを並べる
そうしてこれを行列式で表すと
dX/dt=AX
A=[0,1:-K/M,-c/M]というようになることがわかる
これをscilabで表現してみる
とういうか 行列Aを与えて,それの固有値を見てみる

となる(途中間違えている)
MATLABであれば固有値はeignであったがscilabの場合はspecであるそうな
今回はここまで
シミュレーションの実行にあたって,モデリングがうまく行けば,80%から90%はその仕事が終わったと言って良い.非線形である場合には,解析手法の調整が大変であったりするが,モデルが出来ればそこからは早いのが一般的である.まあ,報告書などをまとめるというのに時間がかかるが,それは別としてである.
簡単な例題からScilabに試させてみよう
図のような一自由度系の簡単な振動系を考える.
数学モデルであるから
上下方向の自由度を表す変数をxとして
Md2x/dt2+Kx+Cdx/dt=0 ....(1)
となる d2x/dt2はxの2回微分 dx/dtは一回微分で,それぞれ加速度,速度を表すことは言うまでもない
モデルとしてxの運動を記述できたわけである.MATLABであればsimlinkを使って積分していけばxの値を計算してグラフに表すのは簡単である.さて,scilabにはどんかToolBoxがあるのか
まずここらへんを調べておかなければならない.
であるが今回は
その前に,基本的な特性がわかるかどうかやってみる
(1)式は,線形の振動方程式であり,その解x=...というのが
解析的に求まる.振動であるから固有振動数があり
それは ω=√K/M (rad/s)であることはわかっている
例えば M=1,000,000kg(=1000ton)とし,k=2000000(N/m)とすると

というようにscilabで計算できる(あたりまえ)
sqrtが√計算で%piがπを表す
ラジアン/sからHzに直しているわけである
私の扱っている機械が1000tくらいあり,それの固有振動数が,0.22Hzくらいであれば逆にこの程度のばね(剛性)をもっているということがわかる
方程式の解がわかっていたのでこんな計算で対象の振動系の特性=固有振動数を調べることができるのであるが,もうすこしシステムとして考えるとどうすれば良いのであろうか
先ほどのToolBoxを使うというのも手であるが(ToolBoxがあるかどうか,これから調べる),数値シミュレーションであれば,方程式が書ければ,それを一次方程式にしてみるということにより一般的になる場合がある.
そこで X=[x,dx/dt]Tというようにベクトルとして位置x,速度dx/dtを並べる
そうしてこれを行列式で表すと
dX/dt=AX
A=[0,1:-K/M,-c/M]というようになることがわかる
これをscilabで表現してみる
とういうか 行列Aを与えて,それの固有値を見てみる

となる(途中間違えている)
MATLABであれば固有値はeignであったがscilabの場合はspecであるそうな
今回はここまで

















※コメント投稿者のブログIDはブログ作成者のみに通知されます