
太陽系に置き換えると太陽と木星のコンビでインターステラーオブジェクトをどれだけ捕まえれるか。捕獲した天体がどれだけの期間太陽系内で過ごすかという事。以下、機械翻訳。
連星系の3体目の捕獲、排出、および拘束された天体の人口統計
2020年12月10日に提出
概要
連星系による任意の速度の軽い物体の捕獲を研究します。太陽の彗星の捕獲のための結果の拡張
システムでは、軌道の分布に直接つながるキャプチャ断面積の単純な幾何学的特性を開発します
キャプチャされたオブジェクトのパラメータ。同じフレームワークを使用して、放出前のこれらの束縛軌道の寿命を調査し、
Öpik–Arnoldアプローチの簡略化されたバージョンは、よく一致する排出率の閉形式の推定値を容易に生成します。
数値実験で。詳細釣り合いの仮定がなければ、私たちの結果はクローズの特徴を明らかにします
捕獲と排出につながる遭遇。結果の応用として、連星系で捕獲された暗黒物質粒子の平衡の推定を示します。
キーワード:天体力学–連星:一般–惑星と衛星:動的進化と安定性
図1.左:テストの単一の3体キャプチャの数値シミュレーション
太陽-木星システムによる粒子。 右:キャプチャされたものの長期的な進化
オブジェクト、軌道パラメータの連続的な変化を示しています

図2.セクション2で想定されている構成と表記法。点線は𝐴𝐵システムの平面にあります。 表記は主にTorbett(1986)に従います。 オブジェクト𝐶、
速度v∞が無限大の場合、影付きの領域で初速度v1のオブジェクト𝐵と接近遭遇し、速度v2で遭遇を終了します。 ご了承ください
描かれたシステムのスケールでは、𝐶の軌道は𝐴による加速のために全体的に湾曲している必要があります。これは簡単にするために省略した機能です。
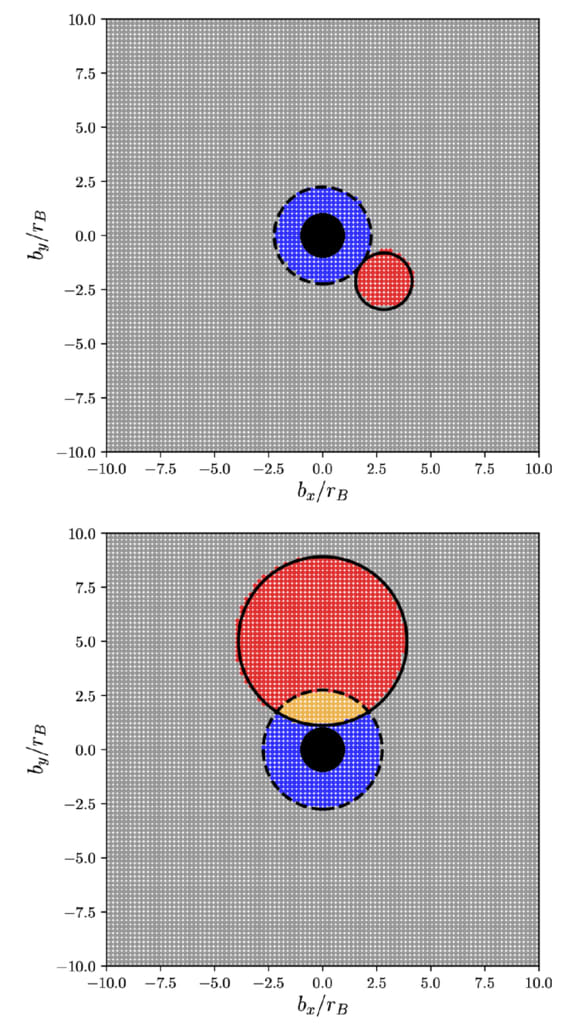
図3.数値積分によって決定された木星との接近遭遇の結果。𝑣∞= 20 km / s、𝛽1 = 𝜋 / 3、および𝜆1の2つの値
上のパネル、𝜆1 = 0、下のパネルでは、𝜆1 = 𝜋 / 2。各ポイントは
異なる衝突パラメータを使用した独立したシミュレーション。ポイントが表示されます
速度vに直交する衝突パラメータの平面内01、つまり、オブジェクト𝐵のフレーム内のオブジェクト𝐶の視点。角度座標
セクション2の処方箋によって修正されます。赤い点はオブジェクトのキャプチャを示します
𝐶、および灰色の点は、オブジェクト𝐶が出発後にバインド解除されたことを示します
接近遭遇地域。オレンジ色の点は、オブジェクト𝐶が木星が点質量に置き換えられた場合に捕獲されたが、代わりに苦しんだ
衝突。青い点は、キャプチャさえも生成しない衝突を示します 木星がある程度圧縮された場合。黒丸は分析を示します
式のキャプチャ領域の予測。 (11)、および破線の円は 式の衝突領域の予測。 (19)。図と比較してください。トーベットの4
(1986)。下のパネルでは、赤い点がごくわずかにシフトしていることに注意してください
分析予測の左側。このシフトは太陽の方向にあります 潮汐力の存在を知らせます。
連星系の3体目の捕獲、排出、および拘束された天体の人口統計
2020年12月10日に提出
概要
連星系による任意の速度の軽い物体の捕獲を研究します。太陽の彗星の捕獲のための結果の拡張
システムでは、軌道の分布に直接つながるキャプチャ断面積の単純な幾何学的特性を開発します
キャプチャされたオブジェクトのパラメータ。同じフレームワークを使用して、放出前のこれらの束縛軌道の寿命を調査し、
Öpik–Arnoldアプローチの簡略化されたバージョンは、よく一致する排出率の閉形式の推定値を容易に生成します。
数値実験で。詳細釣り合いの仮定がなければ、私たちの結果はクローズの特徴を明らかにします
捕獲と排出につながる遭遇。結果の応用として、連星系で捕獲された暗黒物質粒子の平衡の推定を示します。
キーワード:天体力学–連星:一般–惑星と衛星:動的進化と安定性
図1.左:テストの単一の3体キャプチャの数値シミュレーション
太陽-木星システムによる粒子。 右:キャプチャされたものの長期的な進化
オブジェクト、軌道パラメータの連続的な変化を示しています

図2.セクション2で想定されている構成と表記法。点線は𝐴𝐵システムの平面にあります。 表記は主にTorbett(1986)に従います。 オブジェクト𝐶、
速度v∞が無限大の場合、影付きの領域で初速度v1のオブジェクト𝐵と接近遭遇し、速度v2で遭遇を終了します。 ご了承ください
描かれたシステムのスケールでは、𝐶の軌道は𝐴による加速のために全体的に湾曲している必要があります。これは簡単にするために省略した機能です。

図3.数値積分によって決定された木星との接近遭遇の結果。𝑣∞= 20 km / s、𝛽1 = 𝜋 / 3、および𝜆1の2つの値
上のパネル、𝜆1 = 0、下のパネルでは、𝜆1 = 𝜋 / 2。各ポイントは
異なる衝突パラメータを使用した独立したシミュレーション。ポイントが表示されます
速度vに直交する衝突パラメータの平面内01、つまり、オブジェクト𝐵のフレーム内のオブジェクト𝐶の視点。角度座標
セクション2の処方箋によって修正されます。赤い点はオブジェクトのキャプチャを示します
𝐶、および灰色の点は、オブジェクト𝐶が出発後にバインド解除されたことを示します
接近遭遇地域。オレンジ色の点は、オブジェクト𝐶が木星が点質量に置き換えられた場合に捕獲されたが、代わりに苦しんだ
衝突。青い点は、キャプチャさえも生成しない衝突を示します 木星がある程度圧縮された場合。黒丸は分析を示します
式のキャプチャ領域の予測。 (11)、および破線の円は 式の衝突領域の予測。 (19)。図と比較してください。トーベットの4
(1986)。下のパネルでは、赤い点がごくわずかにシフトしていることに注意してください
分析予測の左側。このシフトは太陽の方向にあります 潮汐力の存在を知らせます。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます