
ガス惑星の内部構造を解明するために2百万気圧以上の環境での水素とヘリウムの混ざり具合のシミュレーションを行った。以下、機械翻訳。
木星と土星にヘリウムが降った直接の証拠
概要
温度および圧力条件下での水素-ヘリウム混合物の不混和性
惑星の内部の様子は、巨大ガス惑星の構造を理解するために非常に重要です(例、木星と土星)。
このような極限状態での探査実験は困難を伴いますが、水素の混合挙動を解明するために理論シミュレーションが大きく依存しています。
そしてヘリウム。 ここでは、機械学習による分子加速による手法を開発します。
動的シミュレーションにより、水素とヘリウムの物理的分離を定量化します。
惑星内部の状態。 開発工法により非相溶ラインを実現
1.5 Mbar を超える圧力で以前よりも大幅に高い分離温度が得られます。
理論的なデータですが、実験による推定値によりよく一致します。 私たちの結果は、
H-He の混合が大部分で起こる木星と土星の構造
内部半径、つまり木星では 27.5%、土星では 48.3%。 これは H-He の直接的な証拠です。
不混和層はヘリウムレインの形成をサポートし、ヘリウムの減少を説明します。
木星と土星の大気。
巨大惑星の重力は、私たちの太陽系の形成に重要な役割を果たしています。
木星と土星は、太陽の惑星系の中で最大かつ最も重い巨大ガス惑星です。 現在
木星と土星のモデルは、両方の惑星の構造が組成において類似していることを示唆しています。
目に見える雲の頂上、気体水素、液体水素、金属水素の層が含まれています。
おそらく岩だらけのコア。 ヘリウムは、存在量は異なりますが、水素の 3 つの層すべてに存在します。
ヘリウムと水素の質量密度の合計に対するヘリウムの質量密度の比は 0.238±0.054 です。
の中に木星の大気、0.18~0.255 土星の場合、どちらも推定値よりも決定的に低い
原始太陽ヘリウムの質量分率 (0.275±0.16)。 観察されたヘリウムの減少は、次の原因によって引き起こされると考えられています。
惑星の内部で起こる水素とヘリウムの混合。 ヘリウムの沈殿
より深い層に向かうにつれて、対流を通じて大気中のヘリウムが減少します。 沈没
ヘリウムは、重力位置エネルギーを熱エネルギーに交換することにより、
土星の過剰な明るさに電力を供給する追加のエネルギー源。 したがって、溶解度の完全な図は、
惑星の P-T 条件における水素中のヘリウムは、木星の正確なモデリングに非常に必要です。
土星や他の巨大ガス惑星も同様です。
H-He のレーザーによる衝撃圧縮による巨大惑星モデリングに関する最近の実験
混合物、木星内部の下に H-He 分離の広い領域 (半径範囲の約 15%) が明らかになった
条件。 ただし、以前の第一原理シミュレーション 9 ~ 13 は、より低い分離を示しています。
実験と比較して温度が低く、不混和領域が小さい。 特にデミックスは、
さまざまな理論モデルによって予測される気温は、木星の断熱線のどちらかの側に位置します。
そして土星は2,000Kのオーダーの大きな差異があります。 このような矛盾は完全に
惑星の内部構造のさまざまなモデル。 分離範囲に加えて、分離
惑星モデリングには強度も重要です - 非経験的な計算は過剰な分離を示唆しています
土星の冷却時間が太陽系の寿命より長くなる可能性がある。 理論的には、
混和範囲は通常、混合のギブズ自由エネルギー (ΔG) に基づいて決定されますが、
理論のレベル (非理想的なエントロピー、交換相関関数の選択) はわずかに利益をもたらします。
異なる結果。 一方、物理的分離プロセスは分離において重要な役割を果たします。
水素とヘリウムの影響は考えられますが、これまでの研究では考慮されていませんでした。 この目的のために、私たちは以下を提供します
H-He の物理的分離を定量化し、混和範囲を直接決定する新しい方法
分離プロセスから。 評価を改善するための非平衡アプローチも紹介します。
大規模な系 (約 27,000 原子) の ΔG を計算し、それを使用して混和性を取得します。
ΔG の以前の密度汎関数理論 (DFT) 評価は通常、システム内で実行されます。
すべてのヘリウム部分で十分な混合を確保するために、少数の原子 (数十から数百) を使用します。
そしてP-T条件。 これは従来の計算方法が平衡状態を参照しているためであり、
一方、大規模な系では、特定のヘリウム存在量のギブズ自由エネルギーを表現することはできません。
平衡化中に分離が起こります。 非経験的に分子平衡に達することの難しさ
大規模システムのダイナミクス (MD) シミュレーションにも注目してください。 解像度が低い上に小さい
システムには無視できない熱変動が発生する傾向があり、自由エネルギーの差が不鮮明になる可能性があります。
異なる構成間で。 この問題に対処する 1 つの方法は、統計的サンプリングを可能にするのに十分な数の原子を同時に維持しながら、
第一原理品質。 極限状態の物質を含めた効果的な取り組みが深部で行われた
最近習ったこと15–17。 この研究では、MD シミュレーションは、以下を使用して大幅にスケールアップ (27,000 原子まで) されています。
位置エネルギー面の機械学習表現。 私たちはディープラーニングの可能性を構築しました
(DLP)18 は、van der を使用した強く制約され適切に規範化された (SCAN) 汎関数 19 に基づいています。
rVV1020 からの Waals (vdW) 相互作用。 このスキームは、「両方の長所」を備えた機能として選ばれています。
SCAN は短距離および中距離のインタラクションをキャプチャし、rVV10 は長距離の vdW を記述します。
インタラクション21。 SCAN + rVV10 の組み合わせは、1 kcal/mol よりも優れた精度を有することが示されています。
MP2+ΔCCSD(T) の結果をベンチマークするため、潜在的な潜在的な特性の微妙な特徴を再現できます。
エネルギー面。 可能性とそのベンチマークの詳細については、補足情報を参照してください。
注1.
H-He 混合物の分離挙動は、DLP 加速 MD シミュレーションで捕捉されます。
ただし、MD 軌道の厳密な分析は、視覚的観察を超えて定量化する必要があります。
He が乏しいゾーンと He が豊富なゾーンでの分離。 直感的な平均場法、つまり計算と
システムの小さな部分領域の熱力学特性を平均すると、常に不安定で収束しない結果が得られます。 部分領域を個別に扱うため、部分領域間の相関は無視されます。
そして変動は平滑化されます。 これは、極端に偏ったものを扱う場合にはさらに問題になります。
実際の惑星条件下での組成。 したがって、再重み付けに基づいてアプローチを設計しました。
H-He の分離の範囲を定量化するための「近傍の原子」の条件付き確率 (Pcond)
混合物。 この方法は、体液中の無秩序を測定する方法と同様の統計的戦略に従います。
条件付きエントロピーを使用した混合23。 特定の種類の原子が出現する確率を表にすることで、系内の各原子の近くに存在するため、前述の現象を回避できます。
制限を考慮し、混合と分離のためのより正確な数値基準を取得します。 これの検証は、方法と平均場法との比較については、補足情報注 2 に記載されています。
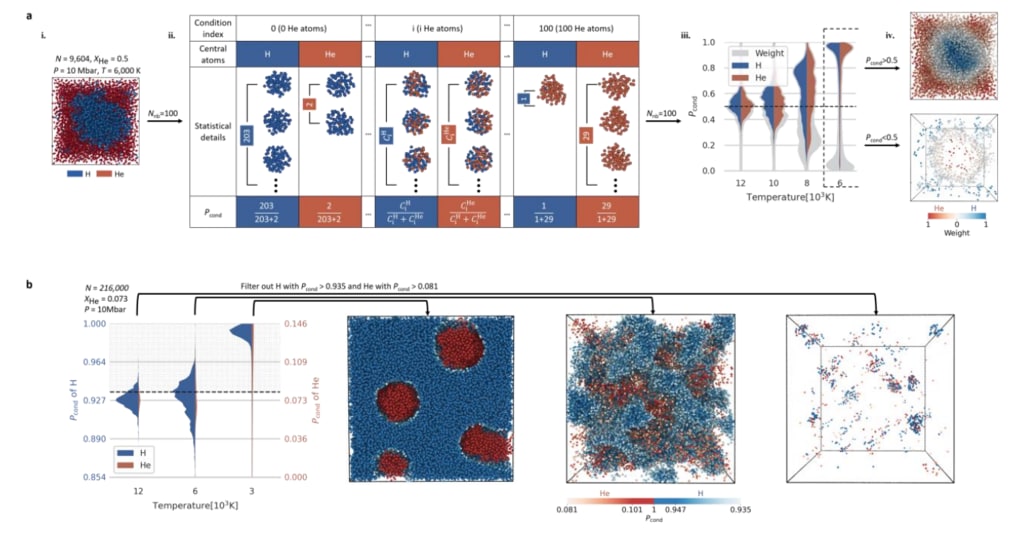
図 1. 再重み付けされた条件付き確率の概略図と利用法。 a, 再重み付けされた値の導出
分子動力学軌道からの条件付き確率。 ステップⅰからⅡまでは、aの近傍です。
中心原子は、最も近い Nnb 周囲原子によって定義されます。 ステップ ii では、すべての近隣が分類されます
すべての原子が水素であることからすべての原子がヘリウムであるまでの原子組成に基づいています。
近傍の各クラスの水素/ヘリウムの Pcond は、この近傍の近傍の確率です。
クラスは水素/ヘリウムを中心としており、その合計は 1 でなければなりません。ステップ ⅲ は、Pcond がどのように計算されるかを示しています。
分布は温度によって変化します。 XHe = 0.5 のシステムの場合、Pcond 値は以下より大きいか小さい
0.5 は、原子がそれ自体または他の元素が豊富な領域にあることを示します。 中心対称のグレー
分布の背後にある影は、次の場合の Pcond 値に対応する各原子の重みを表します。
数えています。 ⅳは、6,000 K ケースの再重み付け分類結果を示しています。 各原子の色は次のことを示します。
その重さ。 b, 極限での再重み付け条件付き確率分類の利用例
偏った組成 ( XHe = 0.073 )。 3 つのシステムを異なる圧力で同じ圧力で準備します。
気温。 各系のすべての原子の Pcond 値を取得した後、Pcond 値を持つヘリウム原子
0.081 より大きい、および 0.935 より大きい Pcond 値を持つ水素原子は、潜在的な H-He の分離の可視化。
この方法の主な概念は、各原子の条件付き確率 (Pcond) を決定することです。
Nnb の最近隣 (近傍) の原子組成に基づくシステム内。 すべての原子
各カテゴリに割り当てられた重みを使用して、条件付き確率によって分類されます。 とともに
分類され再重み付けされた結果 (図 1a)、x1 と x2 は直接計算できます。
{ x1 = N(He He-poor)/ N(He He-poor)+N(H He-poor)
x2 = N(He He-rich)/ N(He He-rich)+N(H He-rich) (1)
値 Δx = x2 − x1
Heが豊富なゾーンとHeが少ないゾーンにおけるヘリウムの存在量の差を表します。
これは非混和性の尺度として使用されます (Δx を使用した非混和性の定義の方法を参照)。
図 1b は、非混和性、弱さを示すための XHe = 0.073 の 3 つの代表的な例を示しています。
この方法を使用して決定される非混和系と混和系。 混和系(12,000Kと2Mbar)、濾過された水素原子とヘリウム原子は数が少なく集まっており、その相を示しています。
分離は起こらず、むしろ対応する領域が大きな変動を示します。 対照的に、
同じ Pcond でフィルタリングされた不混和系は、相分離が蔓延していることを示しています。
シミュレーションボックス。
再重み付けされた条件付き確率を使用して、混合と
LAMMPS24パッケージを使用して計算された大きなH-He混合物のMD軌道における分離挙動
DLP を使用 (シミュレーションの詳細については「方法」を参照)。 システムが動作した後に得られる長時間の軌跡
到達した平衡は、各システムの不混和性の程度を取得するための入力として使用されます。 複数
27,000 原子のシミュレーションで計算された XHe = 0.073 および 0.089 を含むヘリウム存在量が使用されます。
ボックスと XHe = 0.2、0.357、0.5、0.643、0.8、0.91、9,604 原子シミュレーション ボックス。 MD
さまざまな温度と圧力でシミュレーションを実行して、混和図を作成します。
合計 407 の MD 軌道が生成されます。 以前に公開された結果と比較するには9,13、 私たちは
自由計算のための熱力学積分を使用して、4 Mbar および 10 Mbar での混和線も計算しました。
エネルギー ∆G を 64 原子系として計算すると、
∆G(XHe) = G(XHe) − XHeG(1) − (1 − XHe)G(0)。 (2)
x1 と x2 の値は、共通接線構築を ∆G に適用することで決定できます。 の
計算された ∆G と以前の研究の結果 13 との対応する比較は、次の表に示されています。
メソッドセクション。
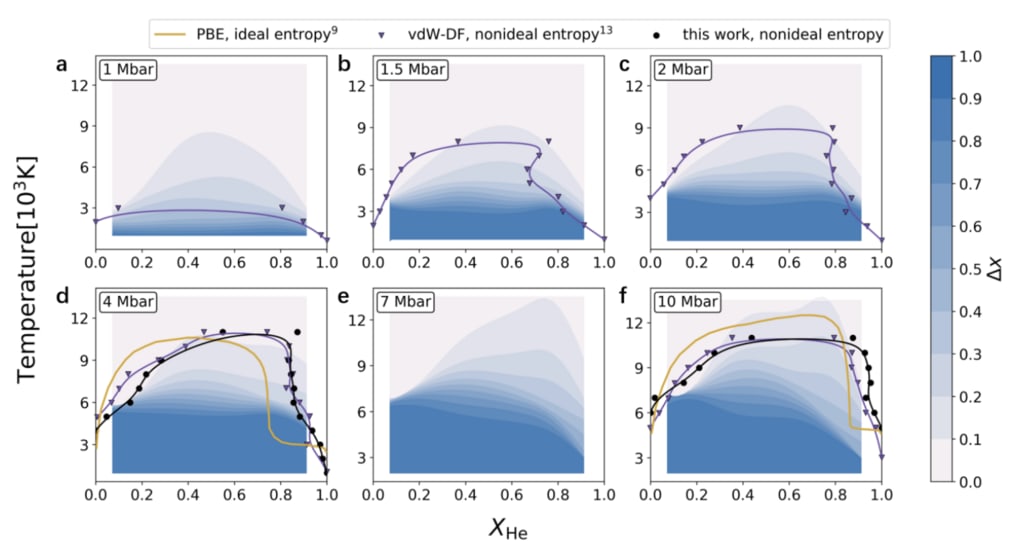
図 2. H-He の混和図。 a、b、c、d、e、f は、圧力 1、1.5、2、4、7、10 に対応します。
ムバール。 色分けされた領域は、再重み付けされた条件式を使用して取得されたさまざまな ∆x ドメインを表します。
分類確率法。 記号と実線は、次の条件によって決定される混和性の境界です。
ΔG の負の曲率。
図 2 に、H-He 混合物のさまざまな組成にわたる混和性図を示します。
異なる圧力で計算されます。 非混和性の尺度 Δx は、0 から均等に分割されます (最小値)。
混和しない) から 1 (最も混和しない)。 4 および 10 Mbar での混和線 (黒い点) が計算されます。
64 原子系の熱力学的積分を使用して以前の研究と比較します。 私たちの結果
vdW-DF と非理想エントロピーを使用して得られた結果と良好な一致を示しています、 とともに
混和線は、He リッチゾーンで高温側にわずかにシフトしています。 この傾向はさらに
PBE および理想エントロピーを使用して得られた結果と比較すると明らかです9。 これらのシフトは、エントロピーの非理想的な効果の結果、He が乏しいゾーンでの分離温度が低下します13
Heリッチゾーンで弱い陽子対を捕捉し、より高い分離温度をもたらします。
さらに、Δx プロファイルは、複数の要因によって引き起こされる H-He 非混和性のかなり複雑な状況を明らかにします。
温度、圧力、原子組成などの要因。 各 Δx ドメインの境界は次のとおりです。
XHe の関数として示され、5 次多項式回帰を使用して平滑化されます。 これらの境界線
中央が盛り上がる一般的な傾向を示しています。 これは、一定の温度で温度が上昇することを示唆しています。
圧力により H-He の混合が起こりますが、中間の XHe 領域で必要な温度はより高くなります。
両端の場合よりも。 さらに、温度誘起混合は XHe に関して対称ではありません。
– Heが少ない領域とHeが豊富な領域では異なる勾配を持っています。 圧力が増加すると、混合性ギャップが増加します
広がり、不混和性が高まります。 ただし、システムが完了すると、変化は徐々に遅くなります。
7Mbarに達しました。 10 Mbar で得られた混和性図では、前者よりもはるかに小さい変化が見られます。
水素とヘリウムの非混和性は、ヘリウムの存在量に非常に敏感であることが観察されています。
惑星の状態。 非常に弱い混和性ギャップによってさえ分離が開始されると、
ヘリウムはプロセスを加速します。 ヘリウムのゆっくりとした沈降が十分な速度に達すると、集中すると、より強い分離が引き起こされる可能性があります。

図 3. 混合率図、ΔG、および木星と土星の影響。 a、混和性図
さまざまなヘリウムの存在量。 XHe = 0.073 の不混和線の下の領域は、
Δx の値。0.0163 は非混和性の閾値と見なされます (「方法」を参照)。 黄色一色と
ピンクの線は、木星と土星の計算された断熱距離であり、以前の結果、木星については黄色の点線 25 と点線 26、土星についてはピンクの点線 26 と点線 27 と並べて表示されます。 によると
以前の研究28–33、3,000 K 未満の白い領域は、水素金属化の推定段階を表します。
b、ヤジンスキーの等価性から木星と土星のヘリウム存在量の周りの∆G。 5つのグラフは、5 つの P-T ポイントで計算された 0.073 を中心とするズームイン存在量領域の ΔG に対応します。 青色は安定領域を表し、赤色は不安定領域および準安定領域を表します。
木星と土星にヘリウムが降った直接の証拠
概要
温度および圧力条件下での水素-ヘリウム混合物の不混和性
惑星の内部の様子は、巨大ガス惑星の構造を理解するために非常に重要です(例、木星と土星)。
このような極限状態での探査実験は困難を伴いますが、水素の混合挙動を解明するために理論シミュレーションが大きく依存しています。
そしてヘリウム。 ここでは、機械学習による分子加速による手法を開発します。
動的シミュレーションにより、水素とヘリウムの物理的分離を定量化します。
惑星内部の状態。 開発工法により非相溶ラインを実現
1.5 Mbar を超える圧力で以前よりも大幅に高い分離温度が得られます。
理論的なデータですが、実験による推定値によりよく一致します。 私たちの結果は、
H-He の混合が大部分で起こる木星と土星の構造
内部半径、つまり木星では 27.5%、土星では 48.3%。 これは H-He の直接的な証拠です。
不混和層はヘリウムレインの形成をサポートし、ヘリウムの減少を説明します。
木星と土星の大気。
巨大惑星の重力は、私たちの太陽系の形成に重要な役割を果たしています。
木星と土星は、太陽の惑星系の中で最大かつ最も重い巨大ガス惑星です。 現在
木星と土星のモデルは、両方の惑星の構造が組成において類似していることを示唆しています。
目に見える雲の頂上、気体水素、液体水素、金属水素の層が含まれています。
おそらく岩だらけのコア。 ヘリウムは、存在量は異なりますが、水素の 3 つの層すべてに存在します。
ヘリウムと水素の質量密度の合計に対するヘリウムの質量密度の比は 0.238±0.054 です。
の中に木星の大気、0.18~0.255 土星の場合、どちらも推定値よりも決定的に低い
原始太陽ヘリウムの質量分率 (0.275±0.16)。 観察されたヘリウムの減少は、次の原因によって引き起こされると考えられています。
惑星の内部で起こる水素とヘリウムの混合。 ヘリウムの沈殿
より深い層に向かうにつれて、対流を通じて大気中のヘリウムが減少します。 沈没
ヘリウムは、重力位置エネルギーを熱エネルギーに交換することにより、
土星の過剰な明るさに電力を供給する追加のエネルギー源。 したがって、溶解度の完全な図は、
惑星の P-T 条件における水素中のヘリウムは、木星の正確なモデリングに非常に必要です。
土星や他の巨大ガス惑星も同様です。
H-He のレーザーによる衝撃圧縮による巨大惑星モデリングに関する最近の実験
混合物、木星内部の下に H-He 分離の広い領域 (半径範囲の約 15%) が明らかになった
条件。 ただし、以前の第一原理シミュレーション 9 ~ 13 は、より低い分離を示しています。
実験と比較して温度が低く、不混和領域が小さい。 特にデミックスは、
さまざまな理論モデルによって予測される気温は、木星の断熱線のどちらかの側に位置します。
そして土星は2,000Kのオーダーの大きな差異があります。 このような矛盾は完全に
惑星の内部構造のさまざまなモデル。 分離範囲に加えて、分離
惑星モデリングには強度も重要です - 非経験的な計算は過剰な分離を示唆しています
土星の冷却時間が太陽系の寿命より長くなる可能性がある。 理論的には、
混和範囲は通常、混合のギブズ自由エネルギー (ΔG) に基づいて決定されますが、
理論のレベル (非理想的なエントロピー、交換相関関数の選択) はわずかに利益をもたらします。
異なる結果。 一方、物理的分離プロセスは分離において重要な役割を果たします。
水素とヘリウムの影響は考えられますが、これまでの研究では考慮されていませんでした。 この目的のために、私たちは以下を提供します
H-He の物理的分離を定量化し、混和範囲を直接決定する新しい方法
分離プロセスから。 評価を改善するための非平衡アプローチも紹介します。
大規模な系 (約 27,000 原子) の ΔG を計算し、それを使用して混和性を取得します。
ΔG の以前の密度汎関数理論 (DFT) 評価は通常、システム内で実行されます。
すべてのヘリウム部分で十分な混合を確保するために、少数の原子 (数十から数百) を使用します。
そしてP-T条件。 これは従来の計算方法が平衡状態を参照しているためであり、
一方、大規模な系では、特定のヘリウム存在量のギブズ自由エネルギーを表現することはできません。
平衡化中に分離が起こります。 非経験的に分子平衡に達することの難しさ
大規模システムのダイナミクス (MD) シミュレーションにも注目してください。 解像度が低い上に小さい
システムには無視できない熱変動が発生する傾向があり、自由エネルギーの差が不鮮明になる可能性があります。
異なる構成間で。 この問題に対処する 1 つの方法は、統計的サンプリングを可能にするのに十分な数の原子を同時に維持しながら、
第一原理品質。 極限状態の物質を含めた効果的な取り組みが深部で行われた
最近習ったこと15–17。 この研究では、MD シミュレーションは、以下を使用して大幅にスケールアップ (27,000 原子まで) されています。
位置エネルギー面の機械学習表現。 私たちはディープラーニングの可能性を構築しました
(DLP)18 は、van der を使用した強く制約され適切に規範化された (SCAN) 汎関数 19 に基づいています。
rVV1020 からの Waals (vdW) 相互作用。 このスキームは、「両方の長所」を備えた機能として選ばれています。
SCAN は短距離および中距離のインタラクションをキャプチャし、rVV10 は長距離の vdW を記述します。
インタラクション21。 SCAN + rVV10 の組み合わせは、1 kcal/mol よりも優れた精度を有することが示されています。
MP2+ΔCCSD(T) の結果をベンチマークするため、潜在的な潜在的な特性の微妙な特徴を再現できます。
エネルギー面。 可能性とそのベンチマークの詳細については、補足情報を参照してください。
注1.
H-He 混合物の分離挙動は、DLP 加速 MD シミュレーションで捕捉されます。
ただし、MD 軌道の厳密な分析は、視覚的観察を超えて定量化する必要があります。
He が乏しいゾーンと He が豊富なゾーンでの分離。 直感的な平均場法、つまり計算と
システムの小さな部分領域の熱力学特性を平均すると、常に不安定で収束しない結果が得られます。 部分領域を個別に扱うため、部分領域間の相関は無視されます。
そして変動は平滑化されます。 これは、極端に偏ったものを扱う場合にはさらに問題になります。
実際の惑星条件下での組成。 したがって、再重み付けに基づいてアプローチを設計しました。
H-He の分離の範囲を定量化するための「近傍の原子」の条件付き確率 (Pcond)
混合物。 この方法は、体液中の無秩序を測定する方法と同様の統計的戦略に従います。
条件付きエントロピーを使用した混合23。 特定の種類の原子が出現する確率を表にすることで、系内の各原子の近くに存在するため、前述の現象を回避できます。
制限を考慮し、混合と分離のためのより正確な数値基準を取得します。 これの検証は、方法と平均場法との比較については、補足情報注 2 に記載されています。

図 1. 再重み付けされた条件付き確率の概略図と利用法。 a, 再重み付けされた値の導出
分子動力学軌道からの条件付き確率。 ステップⅰからⅡまでは、aの近傍です。
中心原子は、最も近い Nnb 周囲原子によって定義されます。 ステップ ii では、すべての近隣が分類されます
すべての原子が水素であることからすべての原子がヘリウムであるまでの原子組成に基づいています。
近傍の各クラスの水素/ヘリウムの Pcond は、この近傍の近傍の確率です。
クラスは水素/ヘリウムを中心としており、その合計は 1 でなければなりません。ステップ ⅲ は、Pcond がどのように計算されるかを示しています。
分布は温度によって変化します。 XHe = 0.5 のシステムの場合、Pcond 値は以下より大きいか小さい
0.5 は、原子がそれ自体または他の元素が豊富な領域にあることを示します。 中心対称のグレー
分布の背後にある影は、次の場合の Pcond 値に対応する各原子の重みを表します。
数えています。 ⅳは、6,000 K ケースの再重み付け分類結果を示しています。 各原子の色は次のことを示します。
その重さ。 b, 極限での再重み付け条件付き確率分類の利用例
偏った組成 ( XHe = 0.073 )。 3 つのシステムを異なる圧力で同じ圧力で準備します。
気温。 各系のすべての原子の Pcond 値を取得した後、Pcond 値を持つヘリウム原子
0.081 より大きい、および 0.935 より大きい Pcond 値を持つ水素原子は、潜在的な H-He の分離の可視化。
この方法の主な概念は、各原子の条件付き確率 (Pcond) を決定することです。
Nnb の最近隣 (近傍) の原子組成に基づくシステム内。 すべての原子
各カテゴリに割り当てられた重みを使用して、条件付き確率によって分類されます。 とともに
分類され再重み付けされた結果 (図 1a)、x1 と x2 は直接計算できます。
{ x1 = N(He He-poor)/ N(He He-poor)+N(H He-poor)
x2 = N(He He-rich)/ N(He He-rich)+N(H He-rich) (1)
値 Δx = x2 − x1
Heが豊富なゾーンとHeが少ないゾーンにおけるヘリウムの存在量の差を表します。
これは非混和性の尺度として使用されます (Δx を使用した非混和性の定義の方法を参照)。
図 1b は、非混和性、弱さを示すための XHe = 0.073 の 3 つの代表的な例を示しています。
この方法を使用して決定される非混和系と混和系。 混和系(12,000Kと2Mbar)、濾過された水素原子とヘリウム原子は数が少なく集まっており、その相を示しています。
分離は起こらず、むしろ対応する領域が大きな変動を示します。 対照的に、
同じ Pcond でフィルタリングされた不混和系は、相分離が蔓延していることを示しています。
シミュレーションボックス。
再重み付けされた条件付き確率を使用して、混合と
LAMMPS24パッケージを使用して計算された大きなH-He混合物のMD軌道における分離挙動
DLP を使用 (シミュレーションの詳細については「方法」を参照)。 システムが動作した後に得られる長時間の軌跡
到達した平衡は、各システムの不混和性の程度を取得するための入力として使用されます。 複数
27,000 原子のシミュレーションで計算された XHe = 0.073 および 0.089 を含むヘリウム存在量が使用されます。
ボックスと XHe = 0.2、0.357、0.5、0.643、0.8、0.91、9,604 原子シミュレーション ボックス。 MD
さまざまな温度と圧力でシミュレーションを実行して、混和図を作成します。
合計 407 の MD 軌道が生成されます。 以前に公開された結果と比較するには9,13、 私たちは
自由計算のための熱力学積分を使用して、4 Mbar および 10 Mbar での混和線も計算しました。
エネルギー ∆G を 64 原子系として計算すると、
∆G(XHe) = G(XHe) − XHeG(1) − (1 − XHe)G(0)。 (2)
x1 と x2 の値は、共通接線構築を ∆G に適用することで決定できます。 の
計算された ∆G と以前の研究の結果 13 との対応する比較は、次の表に示されています。
メソッドセクション。

図 2. H-He の混和図。 a、b、c、d、e、f は、圧力 1、1.5、2、4、7、10 に対応します。
ムバール。 色分けされた領域は、再重み付けされた条件式を使用して取得されたさまざまな ∆x ドメインを表します。
分類確率法。 記号と実線は、次の条件によって決定される混和性の境界です。
ΔG の負の曲率。
図 2 に、H-He 混合物のさまざまな組成にわたる混和性図を示します。
異なる圧力で計算されます。 非混和性の尺度 Δx は、0 から均等に分割されます (最小値)。
混和しない) から 1 (最も混和しない)。 4 および 10 Mbar での混和線 (黒い点) が計算されます。
64 原子系の熱力学的積分を使用して以前の研究と比較します。 私たちの結果
vdW-DF と非理想エントロピーを使用して得られた結果と良好な一致を示しています、 とともに
混和線は、He リッチゾーンで高温側にわずかにシフトしています。 この傾向はさらに
PBE および理想エントロピーを使用して得られた結果と比較すると明らかです9。 これらのシフトは、エントロピーの非理想的な効果の結果、He が乏しいゾーンでの分離温度が低下します13
Heリッチゾーンで弱い陽子対を捕捉し、より高い分離温度をもたらします。
さらに、Δx プロファイルは、複数の要因によって引き起こされる H-He 非混和性のかなり複雑な状況を明らかにします。
温度、圧力、原子組成などの要因。 各 Δx ドメインの境界は次のとおりです。
XHe の関数として示され、5 次多項式回帰を使用して平滑化されます。 これらの境界線
中央が盛り上がる一般的な傾向を示しています。 これは、一定の温度で温度が上昇することを示唆しています。
圧力により H-He の混合が起こりますが、中間の XHe 領域で必要な温度はより高くなります。
両端の場合よりも。 さらに、温度誘起混合は XHe に関して対称ではありません。
– Heが少ない領域とHeが豊富な領域では異なる勾配を持っています。 圧力が増加すると、混合性ギャップが増加します
広がり、不混和性が高まります。 ただし、システムが完了すると、変化は徐々に遅くなります。
7Mbarに達しました。 10 Mbar で得られた混和性図では、前者よりもはるかに小さい変化が見られます。
水素とヘリウムの非混和性は、ヘリウムの存在量に非常に敏感であることが観察されています。
惑星の状態。 非常に弱い混和性ギャップによってさえ分離が開始されると、
ヘリウムはプロセスを加速します。 ヘリウムのゆっくりとした沈降が十分な速度に達すると、集中すると、より強い分離が引き起こされる可能性があります。

図 3. 混合率図、ΔG、および木星と土星の影響。 a、混和性図
さまざまなヘリウムの存在量。 XHe = 0.073 の不混和線の下の領域は、
Δx の値。0.0163 は非混和性の閾値と見なされます (「方法」を参照)。 黄色一色と
ピンクの線は、木星と土星の計算された断熱距離であり、以前の結果、木星については黄色の点線 25 と点線 26、土星についてはピンクの点線 26 と点線 27 と並べて表示されます。 によると
以前の研究28–33、3,000 K 未満の白い領域は、水素金属化の推定段階を表します。
b、ヤジンスキーの等価性から木星と土星のヘリウム存在量の周りの∆G。 5つのグラフは、5 つの P-T ポイントで計算された 0.073 を中心とするズームイン存在量領域の ΔG に対応します。 青色は安定領域を表し、赤色は不安定領域および準安定領域を表します。
c. 影響
木星と土星の場合は、aから。 破線で囲まれた部分は(左)のH-He分離層です。
木星と(右)土星。 青の深さは、青の強度を測定する Δx の値を表します。
H-He 相分離。
図 3a は、現在および以前に公開された結果との混和性図を示しています。 の
原始太陽ヘリウム存在量 (XHe = 0.089) で計算された非混和性ラインがより高い方にシフト
温度を以前の理論的結果と比較したところ11-13、最も近い結果となっています。
実験による推定8
。 ただし、以前の計算では異なるヘリウム存在量が使用され、
実験は注目すべきである。 惑星の断熱は、sJ = 7.613 のエントロピーを使用して計算されます。
木星では kB/原子 25,26、土星では sS = 7.357 kB/原子 26,34。 計算された分離温度 (黒色)
と白い点)は、圧力が 0.5 Mbar から 2 Mbar に増加すると急激に増加します。
水素金属化が始まり、その後平坦になって緩やかな傾斜になります。 この傾向は DFT で示されるものと同じです
計算12、13と実験8。 混和図と断熱図によれば、木星が入ることになる
圧力 1.09 (±0.03) Mbar、温度 5,440 (±50) K における混合性ギャップ。土星の場合、値は 0.93 (±0.03) Mbar および 4,720 (±50) K です。木星の分離領域は約 10,000 K で終了します。
圧力が 10 Mbar (この研究で考慮された最高圧力) のとき、土星はまだ混和状態にあります。
ギャップ。
構造解析から推測される混和性ギャップは非常に広い熱力学的範囲に及びますが、非混和性の強さは比較的弱いです。 これは、ヘリウムの沈降が原因である可能性があることを意味します。
長くて微妙なプロセス。 図 3a では、XHe = 0.089 に対して計算された非混和性ラインは、次の値に対応します。
原始太陽のヘリウムの存在量。 圧力が 1 Mbar を超えると、この不混和線は顕著になります。
XHe = 0.073 よりも高く、He が乏しい領域での Δx の正の傾きと一致しています (図 2)。
原始太陽ヘリウム存在量におけるさまざまな表面温度の等エントロープに基づく14
、計算された
XHe の不混和線 = 0.089 は、土星における H-He 相分離の開始が約 0.746 であることを示唆しています。
ギル。 早期の始まりと段階的な蓄積により、土星は重要な段階を経験する可能性があります
十分な量的変化の後に分離するのに対し、木星でははるかに長い時間を必要とします。 の
原始太陽ヘリウム存在量で計算された混和図は拡張データ図 3 に示されています。
エネルギーの観点を得るために、同じサイズのシステム (27,000 個) を使用して ΔG を計算しました。
5 つの圧力 (0.5、2、4、7、10 Mbar) と温度におけるヘリウム存在量領域のズームイン
5,000 K (図 3b)。 ズームイン領域には、惑星ヘリウム存在量 (XHe = 0.073、プラス記号) が含まれています。
および 8 つの隣接する点 (円)。 計算では、仮想可積分に対する Jarzynski の等式 35 を使用します。
システム36、これにより、分離前の非平衡状態におけるギブズ自由エネルギーの計算が可能になります。
大規模システムでは (ΔG の計算方法を参照)。 0.5 Mbar では、ΔG 曲線上のすべての点が
正の曲率 (二次導関数)。これは、状態が分離せずに安定していることを示唆しています。 2 Mbar では、
小さな負の曲率が ΔG に現れ、デミックスの発生を示します。 分離領域は、
共通接線構造によって決定され、不安定領域と準安定領域 (赤色) に分けられます。
図3bの領域)。 4 Mbar では、ΔG 曲線は依然として下降傾向を示していますが、負の曲率は
相分離が蔓延していることが非常に明白になります。 7 Mbar で、ΔG 曲線が上昇し始め、
制約 ∆G(0) = ∆G(1) = 0 (式 2) に従うと、システムが安定する最小値が少なくとも 2 つ存在します。
10 Mbar では、ΔG 曲線が正の値に上昇し、システム内に強い分離が存在することを示します。
これらの結果は、ΔG の曲率の変化と分離を相関させます。 相分離が最初に現れる
局所的な負の曲率領域で、徐々に進行します
線の形状が進化するにつれて変化します。
これらの結果は、ΔG の曲率の変化と分離を相関させます。 相分離が最初に現れる
負の曲率の局所的な領域では、線の形状が進化するにつれて徐々に進行します。
計算された混和図と惑星モデルを組み合わせる3、内部を導き出しました
木星と土星の構造(図3c)。 木星では、ヘリウムの液滴が存在する水素の液体層
凝縮水と雨は半径の 0.572 ~ 0.847 の間にあると推定されます。 計算された
この層の開始点は実験による推定値 (0.84) に非常に近いです
8 より深い結末がある一方で
組成補正された実験推定値よりも高いポイント (0.68)8。 この不一致の原因は、
理論と実験によって予測される分離温度の異なる挙動(図3a)。 一方、
実験8では、分離温度は2 Mbarを超えて一定に保たれます。
、ゆっくりではありますが継続的に増加しています
理論的には。 土星では、分離層は半径の 0.194 ~ 0.677 の間にあると推定されています。
土星の半径方向の距離のほぼ半分にヘリウムの雨が降ることを示しています。
要約すると、第一原理から H-He 不混和性の直接的な証拠が得られます。 の
機械学習による構造解析により大規模な MD シミュレーションが加速され、新たなシミュレーションが確立されます。
木星と土星の惑星条件下での水素とヘリウムの混和図。 の
水素とヘリウムの不混和性は、温度、圧力、および温度に強く依存することが示されています。
混合物の原子組成。 混和性ギャップは、ギブスの自由エネルギーを使用して再計算されます。
(ΔG) を同じサイズのシステムと混合することで、構造解析が強化されます。 に基づく
その結果、私たちは木星と土星の H-He 分離メカニズムに関する新しい仮説を提案します。
惑星の初期段階での段階的なヘリウムの蓄積によるヘリウム存在量の微妙な増加
この形成により、H-He 相分離が開始される可能性があります。 このプロセスは雨の形成に似ています
集まった雲の中の水滴。 わずかに大きい非混和性とより低い断熱温度
土星の内部では、このプロセスがより起こりやすくなります。 対照的に、木星ではこの前堆積の速度が遅く、断熱温度が高いため、さらなる堆積の可能性が減少します。
分離。

拡張データ 図 1. 非混和性の定義の図。 破線は式です。 5 機能
適切なδでフィッティングします。 黒い中空の円は、20,000 個の軌道からなるランダムに構築された軌道の結果です。
フレーム。 黒い十字は、MD シミュレーションのランダムにシャッフルされた軌跡の結果です。 外側はピンク
領域は系に 9,604 個の原子が含まれる場所を表し、内側の紫色の領域は系が存在する場所です。
27,000個の原子が含まれています。 どちらの色付き領域でも、明るい色から暗い色までが再重み付けの効果を表しています。 木星と土星のヘリウム存在量におけるランダムに構築された軌道の分布は、
差し込み図のオレンジ色の KDE プロット。 黒い縦線はヘリウムの応用例です
P = 2 Mbar に沿って木星と土星が豊富に存在します。 Δx 値を非理想混合系の 𝜇 + 3𝜎 と比較することにより、12,000 K と 8,000 K では系が混合されているのに対し、7,000 K では、6,000 K および 5,000 K のシステムはデミックスしています。
木星と土星の場合は、aから。 破線で囲まれた部分は(左)のH-He分離層です。
木星と(右)土星。 青の深さは、青の強度を測定する Δx の値を表します。
H-He 相分離。
図 3a は、現在および以前に公開された結果との混和性図を示しています。 の
原始太陽ヘリウム存在量 (XHe = 0.089) で計算された非混和性ラインがより高い方にシフト
温度を以前の理論的結果と比較したところ11-13、最も近い結果となっています。
実験による推定8
。 ただし、以前の計算では異なるヘリウム存在量が使用され、
実験は注目すべきである。 惑星の断熱は、sJ = 7.613 のエントロピーを使用して計算されます。
木星では kB/原子 25,26、土星では sS = 7.357 kB/原子 26,34。 計算された分離温度 (黒色)
と白い点)は、圧力が 0.5 Mbar から 2 Mbar に増加すると急激に増加します。
水素金属化が始まり、その後平坦になって緩やかな傾斜になります。 この傾向は DFT で示されるものと同じです
計算12、13と実験8。 混和図と断熱図によれば、木星が入ることになる
圧力 1.09 (±0.03) Mbar、温度 5,440 (±50) K における混合性ギャップ。土星の場合、値は 0.93 (±0.03) Mbar および 4,720 (±50) K です。木星の分離領域は約 10,000 K で終了します。
圧力が 10 Mbar (この研究で考慮された最高圧力) のとき、土星はまだ混和状態にあります。
ギャップ。
構造解析から推測される混和性ギャップは非常に広い熱力学的範囲に及びますが、非混和性の強さは比較的弱いです。 これは、ヘリウムの沈降が原因である可能性があることを意味します。
長くて微妙なプロセス。 図 3a では、XHe = 0.089 に対して計算された非混和性ラインは、次の値に対応します。
原始太陽のヘリウムの存在量。 圧力が 1 Mbar を超えると、この不混和線は顕著になります。
XHe = 0.073 よりも高く、He が乏しい領域での Δx の正の傾きと一致しています (図 2)。
原始太陽ヘリウム存在量におけるさまざまな表面温度の等エントロープに基づく14
、計算された
XHe の不混和線 = 0.089 は、土星における H-He 相分離の開始が約 0.746 であることを示唆しています。
ギル。 早期の始まりと段階的な蓄積により、土星は重要な段階を経験する可能性があります
十分な量的変化の後に分離するのに対し、木星でははるかに長い時間を必要とします。 の
原始太陽ヘリウム存在量で計算された混和図は拡張データ図 3 に示されています。
エネルギーの観点を得るために、同じサイズのシステム (27,000 個) を使用して ΔG を計算しました。
5 つの圧力 (0.5、2、4、7、10 Mbar) と温度におけるヘリウム存在量領域のズームイン
5,000 K (図 3b)。 ズームイン領域には、惑星ヘリウム存在量 (XHe = 0.073、プラス記号) が含まれています。
および 8 つの隣接する点 (円)。 計算では、仮想可積分に対する Jarzynski の等式 35 を使用します。
システム36、これにより、分離前の非平衡状態におけるギブズ自由エネルギーの計算が可能になります。
大規模システムでは (ΔG の計算方法を参照)。 0.5 Mbar では、ΔG 曲線上のすべての点が
正の曲率 (二次導関数)。これは、状態が分離せずに安定していることを示唆しています。 2 Mbar では、
小さな負の曲率が ΔG に現れ、デミックスの発生を示します。 分離領域は、
共通接線構造によって決定され、不安定領域と準安定領域 (赤色) に分けられます。
図3bの領域)。 4 Mbar では、ΔG 曲線は依然として下降傾向を示していますが、負の曲率は
相分離が蔓延していることが非常に明白になります。 7 Mbar で、ΔG 曲線が上昇し始め、
制約 ∆G(0) = ∆G(1) = 0 (式 2) に従うと、システムが安定する最小値が少なくとも 2 つ存在します。
10 Mbar では、ΔG 曲線が正の値に上昇し、システム内に強い分離が存在することを示します。
これらの結果は、ΔG の曲率の変化と分離を相関させます。 相分離が最初に現れる
局所的な負の曲率領域で、徐々に進行します
線の形状が進化するにつれて変化します。
これらの結果は、ΔG の曲率の変化と分離を相関させます。 相分離が最初に現れる
負の曲率の局所的な領域では、線の形状が進化するにつれて徐々に進行します。
計算された混和図と惑星モデルを組み合わせる3、内部を導き出しました
木星と土星の構造(図3c)。 木星では、ヘリウムの液滴が存在する水素の液体層
凝縮水と雨は半径の 0.572 ~ 0.847 の間にあると推定されます。 計算された
この層の開始点は実験による推定値 (0.84) に非常に近いです
8 より深い結末がある一方で
組成補正された実験推定値よりも高いポイント (0.68)8。 この不一致の原因は、
理論と実験によって予測される分離温度の異なる挙動(図3a)。 一方、
実験8では、分離温度は2 Mbarを超えて一定に保たれます。
、ゆっくりではありますが継続的に増加しています
理論的には。 土星では、分離層は半径の 0.194 ~ 0.677 の間にあると推定されています。
土星の半径方向の距離のほぼ半分にヘリウムの雨が降ることを示しています。
要約すると、第一原理から H-He 不混和性の直接的な証拠が得られます。 の
機械学習による構造解析により大規模な MD シミュレーションが加速され、新たなシミュレーションが確立されます。
木星と土星の惑星条件下での水素とヘリウムの混和図。 の
水素とヘリウムの不混和性は、温度、圧力、および温度に強く依存することが示されています。
混合物の原子組成。 混和性ギャップは、ギブスの自由エネルギーを使用して再計算されます。
(ΔG) を同じサイズのシステムと混合することで、構造解析が強化されます。 に基づく
その結果、私たちは木星と土星の H-He 分離メカニズムに関する新しい仮説を提案します。
惑星の初期段階での段階的なヘリウムの蓄積によるヘリウム存在量の微妙な増加
この形成により、H-He 相分離が開始される可能性があります。 このプロセスは雨の形成に似ています
集まった雲の中の水滴。 わずかに大きい非混和性とより低い断熱温度
土星の内部では、このプロセスがより起こりやすくなります。 対照的に、木星ではこの前堆積の速度が遅く、断熱温度が高いため、さらなる堆積の可能性が減少します。
分離。

拡張データ 図 1. 非混和性の定義の図。 破線は式です。 5 機能
適切なδでフィッティングします。 黒い中空の円は、20,000 個の軌道からなるランダムに構築された軌道の結果です。
フレーム。 黒い十字は、MD シミュレーションのランダムにシャッフルされた軌跡の結果です。 外側はピンク
領域は系に 9,604 個の原子が含まれる場所を表し、内側の紫色の領域は系が存在する場所です。
27,000個の原子が含まれています。 どちらの色付き領域でも、明るい色から暗い色までが再重み付けの効果を表しています。 木星と土星のヘリウム存在量におけるランダムに構築された軌道の分布は、
差し込み図のオレンジ色の KDE プロット。 黒い縦線はヘリウムの応用例です
P = 2 Mbar に沿って木星と土星が豊富に存在します。 Δx 値を非理想混合系の 𝜇 + 3𝜎 と比較することにより、12,000 K と 8,000 K では系が混合されているのに対し、7,000 K では、6,000 K および 5,000 K のシステムはデミックスしています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます