
ミマスとリングで平均運動共鳴によりリング内に波が起こる。以下、機械翻訳。
ミマス 5:3 屈曲波で自己重力の力学が目覚める: 線形理論の修正
要約
衛星ミマスは、放射状に伝播するリングの歪みである曲げ波を発射します。
自己重力を通して、土星の輪との5:3の内部垂直共鳴で。 私たちは、
次の効果を含む線形屈曲波理論 (Shu et al. 1983) の修正
衛星の自己重力は波の中の粒子上で目覚めます。 次のように扱うと、それが示されます。
硬い場合、これらの後流は粒子の追加層を生成し、その数密度は比例します。
歪んだリングの傾きの大きさに応じて変化します。 レイトレーシング コードを使用して、
Shuらの予測と一致する。 (1983) と 60 個の恒星掩蔽が観測されました。
カッシーニ紫外イメージング分光器 (UVIS) を使用して、粒子の余分な層が存在することを発見しました。
摂動曲げ波モデルの UVIS に対するかなりの説明力があります。
データセット。 私たちの最良のモデルは、ミマスの最も矛盾した驚くべき機能を説明します
5:3 ベンディングウェーブ。 高高度の掩蔽の場合の信号の強化
リングの開き角度と予想よりも大きな粘度、ν = 576 cm^2/s です。
密度波から計算された粘度の 2 倍より大きくなります (Tiscareno et al. 2007)。 これは示しています
自己重力伴流は角運動量を垂直方向に輸送するのに効果的である可能性がある
乱れたディスク。 隣接する密度波と比較すると (Tiscareno et al. 2007)、
表面質量密度の予想値より低い値、σ = 36.7 g/cm^2
、これは次のことを示唆しています
強化された粘性相互作用により、物質が周囲の領域に輸送されている可能性があります。
キーワード: 土星、惑星環、天力学、恒星食、土星の衛星
1. はじめに
屈曲波 (BW) は、摂動によって引き起こされる円盤 (円形で薄い質量面) の歪みです。
自己重力によって伝播する円盤に対して垂直です。 歪んだ円盤は天体物理学のいたるところに存在しており、
若い星 (Epstein-Martin et al. 2022)、ブラックホール (Thomas et al. 2021)、およびその周囲で発見される
惑星 (Shu et al. 1983) については、膨大な量の観測が利用可能です。 ワープは限られた範囲でしか理解されていませんが (たとえば、Nelson & Tremaine 1995 を参照)、ワープは次の場合に発生することが知られています。
面外の力は、中心体の周りを周回する円盤を乱します。 土星の輪の場合、傾いた軌道を持つ衛星がある周波数で輪の粒子を乱すときに面外力が発生します。
これは、土星からのある半径方向の距離におけるこれらの粒子の垂直運動の有理数倍と一致します。
(マレーとダーモット、2000)。 これらの共鳴の多くは土星の環の中で発生します。
土星の中心から131902kmの衛星ミマスによる5:3の垂直共鳴。 放射状のカット
理想的な屈曲波を図 1 の上のパネルに示します。
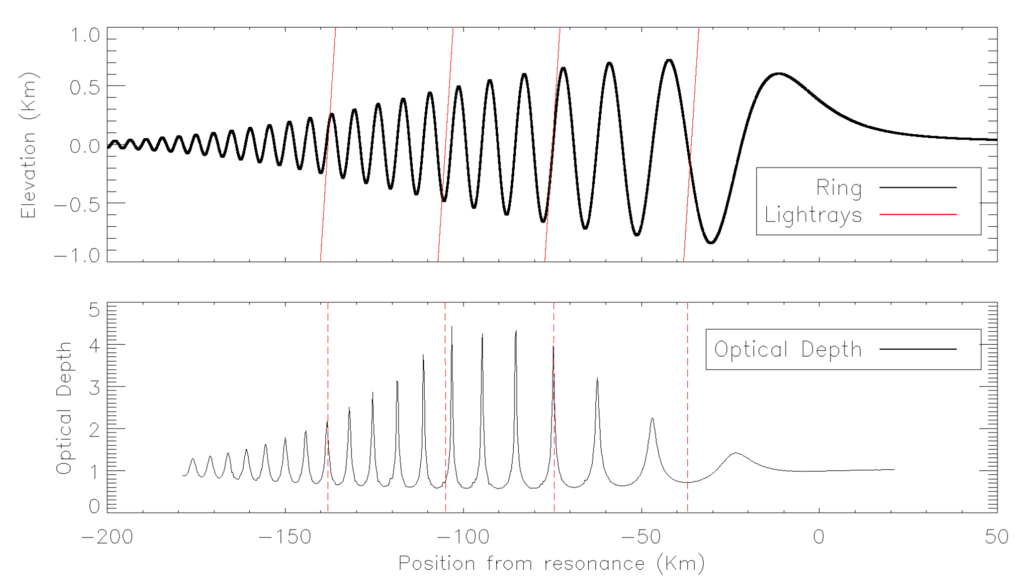
図 1. 垂直変位 (上のパネル) と見かけの光学的深さ (下のパネル) の理論的予測
SCLによると。 上部パネルの赤い光線はリングを透過する光線を表しており、
各光線に対してプローブされた対応する光学的深さは、下部パネルの赤い破線でマークされています。 の
平均リング平面と入射光線の間の角度は B = 26°です
(軸は同じではないことに注意してください
スケール)、半径方向と平面に投影された光線との間の角度は ϕ = 0 です。
。 見える
光線がリングの傾斜(図のピークに相当)と一致するときに、より多くの物質をどのように通過するか
光学的深さ)、および斜面(谷に相当する)に垂直に移動するときに材料を通過する量が少なくなります。
光学的深さ)。
Shu、Cuzzi、および Lissauer (1983) (以下、SCL) は、屈曲波の存在を最初に確認しました。
Bertin & Mark (1980) によって開発された歪んだ銀河の理論を適用し、分析することにより、リング内で
ボイジャー I からの画像。弱い曲げ波については SCL 理論に一般的に同意しましたが、
ミマス 5:3 BW は適合するのが難しいことがわかりました。 その後、Lissauer ら。 (1984) この特定の波に焦点を当て、
同様の方法を使用して粘度の値を取得しました。 掩蔽を利用した波の一般的研究
ボイジャーの偏光計からの解析はその後、エスポジトらによって行われました。 (1983)、Gresh et al。 (1986)は
低開口角電波掩蔽を使用した屈曲波に焦点を当てた広範な研究。 どちらも管理されていない
Mimas 5:3 BW の形状を説明するために、Gresh et al. (1986) は、減衰メカニズムが
この波には修正が必要です。 理論面では、Chakrabarti (1988、1989) は半径方向せん断を考慮しました。
Mimas 5:3 BW の減衰機構として粒子の分散を調整しましたが、粘度に関しては一貫性のない結果が得られました。 これらの取り組みはすべてボイジャーの観測に基づいています。 ただし、カッシーニのデータはまだ
屈曲波の理論を改善するために使用されます。
図 1 は、恒星掩蔽によって測定されるリングの光学的深さに BW がどのように影響するかを示しています。
(これは、リングによって覆われている星の測光測定値です) リングが次のように動作すると仮定します。
SCL理論によって予測されています。 下のパネルの赤い破線は、対応する光学深度を示しています。
上部パネルの光線に対して: 光線が最も大きいときに光学的深さの最大値 (最小値) が発生します。
局所的に歪んだリングに対して平行(垂直)。 カッシーニ掩蔽 (図 2 と 3) を見ると、
そしてGreshらと比較することによって。 (1986) では、SCL を比較するときに現れる 3 つの問題を特定しました。
データを使用して:
(1) 波形プロファイル。
波の形態の予測が不十分であることは、図 2 で観察できます。
UVIS によって測定された γ-ペガサス星掩蔽の光学的深さ (赤線) と SCL 理論との比較
(黒い線)。 掩蔽の有効開口角は Beff = Tan−1 として定義されます。
(tan B/cos ϕ) ここで
B は平均リング平面と入射光線の間の角度、ϕ は半径方向の角度です。
方向と平面に投影された光線 (Gresh et al. 1986 を参照)。 Beff が低いほど、高い
光学的深さの変化。 図 1 に示すように、この光学的深さの山と谷は次のように依存します。
星への視線に対するリングの傾き、または傾き。 の過剰予測
図 2 に見られる -80 km までの光学深さのピーク内部は、SCL 理論がこれを過大評価していることを示唆しています。
傾斜。
SCL はまた、フラット リングに対するディスクの光学的深さのすべての変動は、単にリングのみによって引き起こされると予測しています。
リングの傾きによって。 したがって、視線がリングに対して垂直である掩蔽では、
光学的深さの変動が予想されます。 しかし、図 3 の左側のパネルでは、データはそうではないことを示しています。
(リングに対して) ほぼ垂直な掩蔽は依然として光学的深さの対称的な変化を示します。
これは、リング内の粒子の断片化によって引き起こされる可能性のある追加の物質層が BW 内に生成されていることを示唆しています (Gresh et al. 1986)。
図 3 の右パネルは、この光学的深さのピークの位置と全体の形状を示しています。
強調は、波の最大傾きの理論的予測と相関しています (黒く塗りつぶされます)。
これは、この断片化が
リングの傾斜が急な場所ほど高くなります。 この研究では、私たちは、次のようなもっともらしい物理メカニズムを提案します。
は、この追加の粒子層と、波の傾きとの明らかな相関関係を説明しています。
これは、可視粒子間の比較として、粒子の余分な層がヘイズとして説明できることを示唆しています。
赤外線マッピング分光計 (VIMS) と UVIS データ (表 1 を参照) は、微量の物質の存在を示しています。
検出器からの赤外線光を回折させて赤外線を増加させるサブミリメートルサイズの粒子の量
光学的深さ (Jerousek et al. 2016)。 通常はサブミリ粒子であるため、これはAリングでは珍しい光景です。
急速に降着してより大きな粒子になり (Bodrova et al. 2012; Harbison et al. 2013)、
BW 領域における物質の破壊を説明する SCL 理論の修正。
(2) 共鳴に近い波長。
図 2 は、理論上の波長が後の波頭 (この波) ではかなりうまく機能することを示しています。
プロットでは左に伝播します)、共鳴付近の観測値とは異なります。Gresh で見られる結果です。
他。 (1986年)。 図 3 と表 1 で示唆されている追加の粒子層は、半径方向の変化を引き起こす可能性があります。
表面密度 - 局所波長に影響を与える (SCL; Lehmann et al. 2019) - または形状を変更する
最初の光学的深さのピーク。 これらの効果は、観察された波長の不一致を説明するのに役立つ可能性があります。
ミマス 5:3 屈曲波で自己重力の力学が目覚める: 線形理論の修正
要約
衛星ミマスは、放射状に伝播するリングの歪みである曲げ波を発射します。
自己重力を通して、土星の輪との5:3の内部垂直共鳴で。 私たちは、
次の効果を含む線形屈曲波理論 (Shu et al. 1983) の修正
衛星の自己重力は波の中の粒子上で目覚めます。 次のように扱うと、それが示されます。
硬い場合、これらの後流は粒子の追加層を生成し、その数密度は比例します。
歪んだリングの傾きの大きさに応じて変化します。 レイトレーシング コードを使用して、
Shuらの予測と一致する。 (1983) と 60 個の恒星掩蔽が観測されました。
カッシーニ紫外イメージング分光器 (UVIS) を使用して、粒子の余分な層が存在することを発見しました。
摂動曲げ波モデルの UVIS に対するかなりの説明力があります。
データセット。 私たちの最良のモデルは、ミマスの最も矛盾した驚くべき機能を説明します
5:3 ベンディングウェーブ。 高高度の掩蔽の場合の信号の強化
リングの開き角度と予想よりも大きな粘度、ν = 576 cm^2/s です。
密度波から計算された粘度の 2 倍より大きくなります (Tiscareno et al. 2007)。 これは示しています
自己重力伴流は角運動量を垂直方向に輸送するのに効果的である可能性がある
乱れたディスク。 隣接する密度波と比較すると (Tiscareno et al. 2007)、
表面質量密度の予想値より低い値、σ = 36.7 g/cm^2
、これは次のことを示唆しています
強化された粘性相互作用により、物質が周囲の領域に輸送されている可能性があります。
キーワード: 土星、惑星環、天力学、恒星食、土星の衛星
1. はじめに
屈曲波 (BW) は、摂動によって引き起こされる円盤 (円形で薄い質量面) の歪みです。
自己重力によって伝播する円盤に対して垂直です。 歪んだ円盤は天体物理学のいたるところに存在しており、
若い星 (Epstein-Martin et al. 2022)、ブラックホール (Thomas et al. 2021)、およびその周囲で発見される
惑星 (Shu et al. 1983) については、膨大な量の観測が利用可能です。 ワープは限られた範囲でしか理解されていませんが (たとえば、Nelson & Tremaine 1995 を参照)、ワープは次の場合に発生することが知られています。
面外の力は、中心体の周りを周回する円盤を乱します。 土星の輪の場合、傾いた軌道を持つ衛星がある周波数で輪の粒子を乱すときに面外力が発生します。
これは、土星からのある半径方向の距離におけるこれらの粒子の垂直運動の有理数倍と一致します。
(マレーとダーモット、2000)。 これらの共鳴の多くは土星の環の中で発生します。
土星の中心から131902kmの衛星ミマスによる5:3の垂直共鳴。 放射状のカット
理想的な屈曲波を図 1 の上のパネルに示します。

図 1. 垂直変位 (上のパネル) と見かけの光学的深さ (下のパネル) の理論的予測
SCLによると。 上部パネルの赤い光線はリングを透過する光線を表しており、
各光線に対してプローブされた対応する光学的深さは、下部パネルの赤い破線でマークされています。 の
平均リング平面と入射光線の間の角度は B = 26°です
(軸は同じではないことに注意してください
スケール)、半径方向と平面に投影された光線との間の角度は ϕ = 0 です。
。 見える
光線がリングの傾斜(図のピークに相当)と一致するときに、より多くの物質をどのように通過するか
光学的深さ)、および斜面(谷に相当する)に垂直に移動するときに材料を通過する量が少なくなります。
光学的深さ)。
Shu、Cuzzi、および Lissauer (1983) (以下、SCL) は、屈曲波の存在を最初に確認しました。
Bertin & Mark (1980) によって開発された歪んだ銀河の理論を適用し、分析することにより、リング内で
ボイジャー I からの画像。弱い曲げ波については SCL 理論に一般的に同意しましたが、
ミマス 5:3 BW は適合するのが難しいことがわかりました。 その後、Lissauer ら。 (1984) この特定の波に焦点を当て、
同様の方法を使用して粘度の値を取得しました。 掩蔽を利用した波の一般的研究
ボイジャーの偏光計からの解析はその後、エスポジトらによって行われました。 (1983)、Gresh et al。 (1986)は
低開口角電波掩蔽を使用した屈曲波に焦点を当てた広範な研究。 どちらも管理されていない
Mimas 5:3 BW の形状を説明するために、Gresh et al. (1986) は、減衰メカニズムが
この波には修正が必要です。 理論面では、Chakrabarti (1988、1989) は半径方向せん断を考慮しました。
Mimas 5:3 BW の減衰機構として粒子の分散を調整しましたが、粘度に関しては一貫性のない結果が得られました。 これらの取り組みはすべてボイジャーの観測に基づいています。 ただし、カッシーニのデータはまだ
屈曲波の理論を改善するために使用されます。
図 1 は、恒星掩蔽によって測定されるリングの光学的深さに BW がどのように影響するかを示しています。
(これは、リングによって覆われている星の測光測定値です) リングが次のように動作すると仮定します。
SCL理論によって予測されています。 下のパネルの赤い破線は、対応する光学深度を示しています。
上部パネルの光線に対して: 光線が最も大きいときに光学的深さの最大値 (最小値) が発生します。
局所的に歪んだリングに対して平行(垂直)。 カッシーニ掩蔽 (図 2 と 3) を見ると、
そしてGreshらと比較することによって。 (1986) では、SCL を比較するときに現れる 3 つの問題を特定しました。
データを使用して:
(1) 波形プロファイル。
波の形態の予測が不十分であることは、図 2 で観察できます。
UVIS によって測定された γ-ペガサス星掩蔽の光学的深さ (赤線) と SCL 理論との比較
(黒い線)。 掩蔽の有効開口角は Beff = Tan−1 として定義されます。
(tan B/cos ϕ) ここで
B は平均リング平面と入射光線の間の角度、ϕ は半径方向の角度です。
方向と平面に投影された光線 (Gresh et al. 1986 を参照)。 Beff が低いほど、高い
光学的深さの変化。 図 1 に示すように、この光学的深さの山と谷は次のように依存します。
星への視線に対するリングの傾き、または傾き。 の過剰予測
図 2 に見られる -80 km までの光学深さのピーク内部は、SCL 理論がこれを過大評価していることを示唆しています。
傾斜。
SCL はまた、フラット リングに対するディスクの光学的深さのすべての変動は、単にリングのみによって引き起こされると予測しています。
リングの傾きによって。 したがって、視線がリングに対して垂直である掩蔽では、
光学的深さの変動が予想されます。 しかし、図 3 の左側のパネルでは、データはそうではないことを示しています。
(リングに対して) ほぼ垂直な掩蔽は依然として光学的深さの対称的な変化を示します。
これは、リング内の粒子の断片化によって引き起こされる可能性のある追加の物質層が BW 内に生成されていることを示唆しています (Gresh et al. 1986)。
図 3 の右パネルは、この光学的深さのピークの位置と全体の形状を示しています。
強調は、波の最大傾きの理論的予測と相関しています (黒く塗りつぶされます)。
これは、この断片化が
リングの傾斜が急な場所ほど高くなります。 この研究では、私たちは、次のようなもっともらしい物理メカニズムを提案します。
は、この追加の粒子層と、波の傾きとの明らかな相関関係を説明しています。
これは、可視粒子間の比較として、粒子の余分な層がヘイズとして説明できることを示唆しています。
赤外線マッピング分光計 (VIMS) と UVIS データ (表 1 を参照) は、微量の物質の存在を示しています。
検出器からの赤外線光を回折させて赤外線を増加させるサブミリメートルサイズの粒子の量
光学的深さ (Jerousek et al. 2016)。 通常はサブミリ粒子であるため、これはAリングでは珍しい光景です。
急速に降着してより大きな粒子になり (Bodrova et al. 2012; Harbison et al. 2013)、
BW 領域における物質の破壊を説明する SCL 理論の修正。
(2) 共鳴に近い波長。
図 2 は、理論上の波長が後の波頭 (この波) ではかなりうまく機能することを示しています。
プロットでは左に伝播します)、共鳴付近の観測値とは異なります。Gresh で見られる結果です。
他。 (1986年)。 図 3 と表 1 で示唆されている追加の粒子層は、半径方向の変化を引き起こす可能性があります。
表面密度 - 局所波長に影響を与える (SCL; Lehmann et al. 2019) - または形状を変更する
最初の光学的深さのピーク。 これらの効果は、観察された波長の不一致を説明するのに役立つ可能性があります。
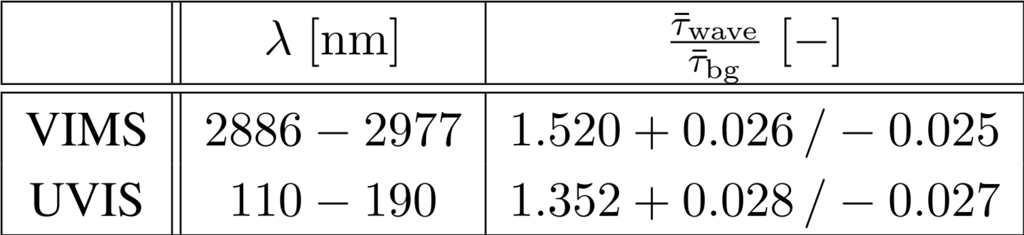
表 1. VIMS および UVIS 機器によって撮影された、さそり座αの赤外線と紫外線の同時掩蔽。
VIMS の光学深さは UVIS と比較して 13% 大きいです。 τbg については、131600 ~ 131700 km のデータを平均しました。
τwave については、131862 km から 131762 km までのデータを平均しました。
VIMS の光学深さは UVIS と比較して 13% 大きいです。 τbg については、131600 ~ 131700 km のデータを平均しました。
τwave については、131862 km から 131762 km までのデータを平均しました。

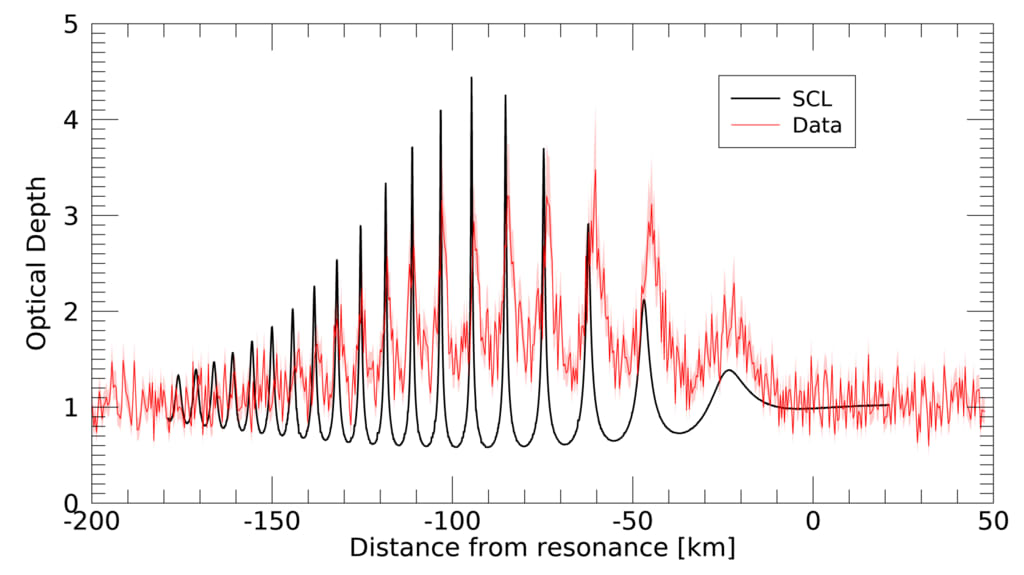
図 2. γ-ペガサスの掩蔽を比較します (rev 32I、B = 20.3◦、ベフ = 26°) カッシーニ (赤) から見た
標準的な屈曲波理論 (黒)。 半径131,902kmで共鳴が起こり波が伝播
土星に向かって(プロットの左側)。 3 つの大きな矛盾が見られます: (1) SCL 理論は、ピークを過剰予測します。
光学的深度が低く、谷を過小予測します。 (2) 最初の 3 サイクルでは波長が一致しません。 (3) 理論
ピークはまだ-150 km付近に現れると予測されているため、波が減衰する速度を過小予測していますが、観測された波は
その前にノイズに埋もれてしまいます。 Lissauer らの粘度 ν = 260 cm2/s を使用します。 (1984) の分析
この波とTiscarenoら。 (2007) によるプロメテウス 11:12 密度波の分析。
(3) 粘度。
リングの粘度は、図に見られる光学的深さプロファイルのピークの形状と振幅を制御します。
図 2. 粘性相互作用によりリング粒子の垂直方向の変位が減少します。 それによって、今度は
リングの傾斜と視線が一致する点での最大消光。 言い換えれば、
光学的深さパターンのピーク振幅は粘度に依存します。 図 2 の SCL モデル (黒線)
ピークの多い光学的深さプロファイルと、観察された変動を超えて伝播する波を予測します
データに見られます (赤い線)。 これは、減衰の流体せん断の説明が不十分であること、および/または
以前の Mimas 5:3 BW 研究 (Lissauer et al. 1984; Gresh et al. 1986) および Cassini によって示唆された値
密度波の研究 (Tiscareno et al. 2007) では、この波を説明するには低すぎます。 それにもかかわらず、観察された
光学的深さのピークと波の減衰の速さは、現在の理論が波の領域に拡散するエネルギーと運動量の量を過小予測していることを示しています。 この拡散の欠落は、次の原因によって引き起こされる可能性があります。
図 3 で示唆されている追加の粒子層を生成するメカニズムと同じです。
3 つの問題はすべて、カッシーニのリング掩蔽データを使用して詳しく調べることができます。 カッシーニがミマ星を観測
UVIS 高速光度計 (HSP) (Esposito et al. 2004) を使用した 217 回の掩蔽で 5:3 BW
これら 130 は、屈曲波によるデータの変化を検出するのに十分な高い S/N 比を持っています。
さらに、Cassini データを使用して、Colwell et al. (2006) は自己重力航跡の存在を確認しました。
周期的に凝集し、典型的な A 粒子よりも 10 ~ 100 倍大きい粒子の細長い塊。
リング粒子(〜 1 m)(Jerousek et al. 2016; Salo et al. 2018)。 自己重力覚醒を追加した結果
SCL 理論への影響は、関連するトルクに剛体として反応するという仮定を介してセクション 2 で導き出されます。
天体。 ここで我々は、通常の掩蔽で見られる追加の光学的深度信号を説明するメカニズムを提示します。
セクション §3 では、透過モデル、使用される 60 個の UVIS 掩蔽の選択基準について説明します。
データがどのように削減されたか。 セクション §4 では、レイ トレーシング コードについて説明します。 セクション §5 で比較します。
屈曲波モデルをデータに当てはめた後、セクション 6 で説明します。
このモデルは上記の問題を解決します。 セクション §7 で結論を要約します。
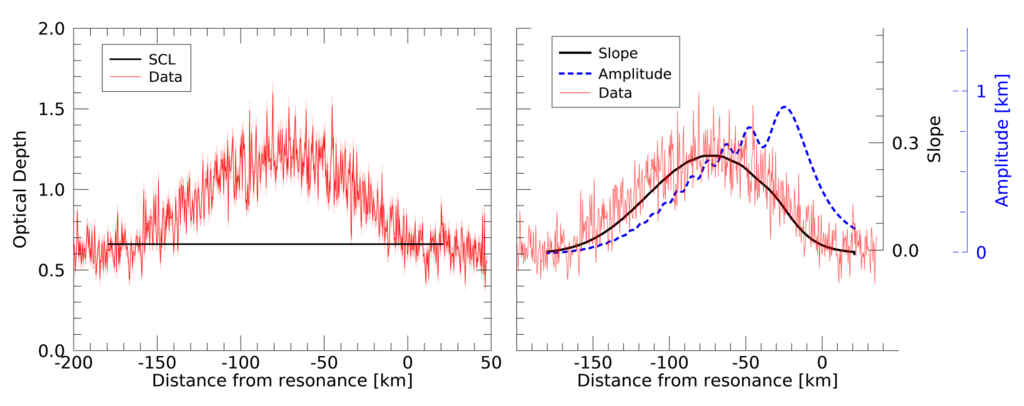
図 3. 左のパネル: β-ケンタウリの掩蔽を比較します (rev85I、B = 66.7◦、ベフ = 87°) (赤く点灯)、
SCLモデル(ソリッドバック)。 エラーバーは、プロットの背景に薄赤色の塗りつぶされた曲線として表示されます。 の
SCL 理論は均一な光学的深さを予測します。 ただし、データは、中心を中心とした光学的深さの対称的な上昇を示しています。
共鳴から−80km。 右パネル: β-Centauri の同じ光学深度プロファイル (赤色の実線) が、β-Centauri の光学深度プロファイルと比較されています。
理論的 (SCL 理論) の波の最大傾き (黒の実線) と波の振幅 (青の破線)
粘度 566 cm2/s、リング表面密度 σ = 36.3 g/cm2; これらの値は、この論文で紹介されているモデル。
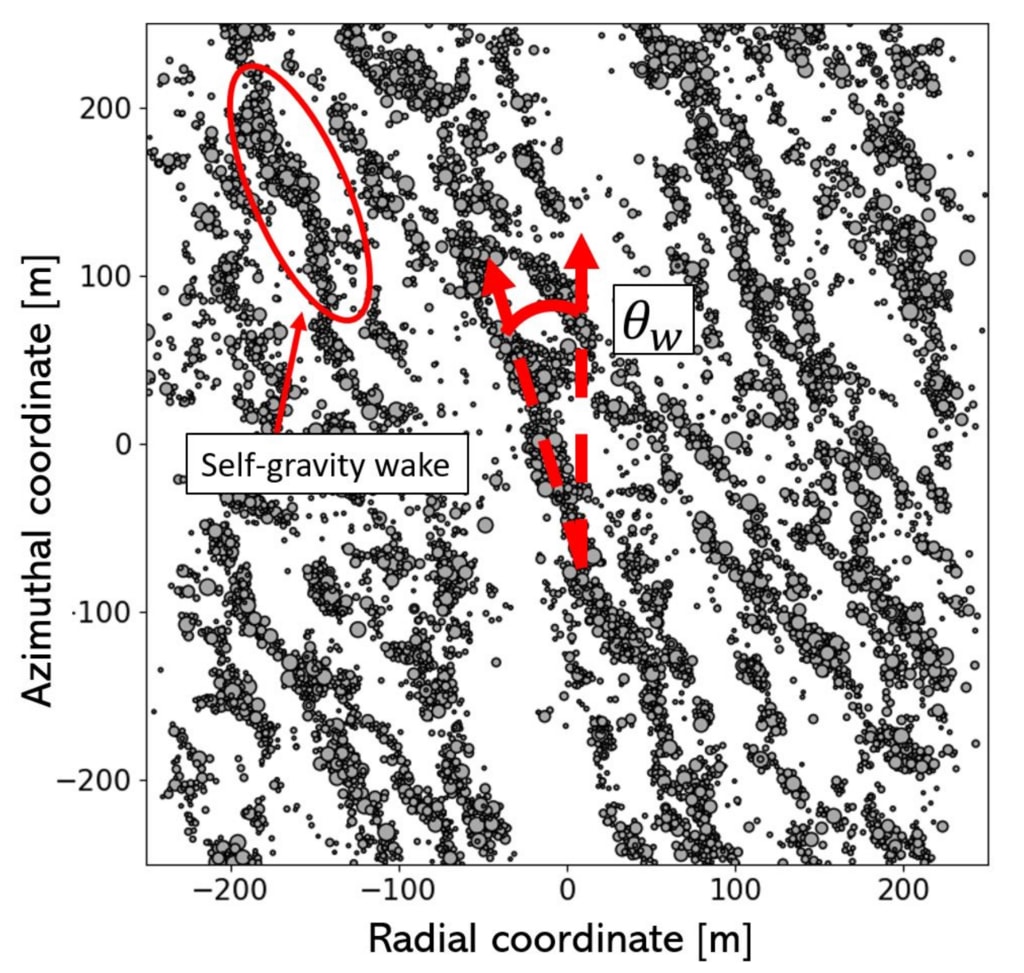
図 4. シアーシート REBOUND の例で生成されたシアーボックス シミュレーションにおける自己重力ウェイクのスナップショット
(Rein & Liu 2012)、視覚化のみを目的としています。 赤で囲まれた部分には、指向性のある自己重力の航跡が見られます。 我々はできる
また、それらは方位角に対して角度 θw を指す傾向があることもわかります。
2. 自己重力後流と屈曲波
自己重力後流は、方位角から角度 θw の細長い構造を持つ粒子の塊です。
これらは、ケプラーせん断に抗して自己重力によって一緒に保持されます (図 4 を参照)。
構成粒子は、相対距離の変更に対する抵抗を示します (Δrij ≈ 0) (Daisaka & Ida 1999;ルーら。 2018)。
言い換えれば、航跡内の粒子は一貫した動きを示し、航跡は一定の速度を維持します。
1 軌道周期の時間スケールでの形状と方向の一貫性 (Karjalainen & Salo 2004)。 自己重力
航跡は、銀河系の文脈で非軸対称の擾乱として初めて仮説が立てられました (Toomre 1964)。
回転ディスクの自己重力とそのせん断の相互作用によって生成されます。 彼らが最初に提案したのは、
Colombo et al. によるリングに存在します。 (1976)、および Dones & Porco (1989)、および Dunn et al. (2004) は、ボイジャー画像と超大型アレイ観測に対するそれらの影響をそれぞれモデル化し、裏付けました。 彼らはいた
惑星環はサロ (1992) によって初めて数値モデル化され、コルウェルの土星の環で検出されました。
他。 (2006) UVIS 掩蔽の光学的深さにおける方位角の非対称性として。
SCL 線形屈曲波理論では、リングが滑らかで密度が均一であるとみなします。
これらの構造は力学では考慮されていませんでした。 自己重力覚醒の影響を研究するために、
少なくとも波が波内で 1 波長進むのにかかる時間の間は、それらは堅いままであると仮定します。
フレームは航跡と共回転し、これは約 1 軌道周期です (以下の式 5 を参照)。 少なくとも一部の自己重力航跡は、その期間にわたって一緒に留まることが予想されます (Karjalainen & Salo 2004): シミュレーションでも
多くの軌道周期の可能性のある寿命を示唆しています (Michibashi et al. 2015)。
BW 内では、後流は方向 (θq) に影響を与えるさまざまなトルクを受けます。
'、図 5 を参照)
波に合わせて高度 (z) に振動します。 これらのトルクとその回転運動への影響
航跡はセクション §2.1 で計算されます。 航跡が方向を変えるにつれて、航跡が
後流の中心からある程度の距離にある粒子は、後流との垂直速度に差が生じます。
周囲のリング粒子 (予想される SCL の垂直方向の動きに従うと想定されます)、その結果、
相対速度が 1 cm/s 程度の衝突で、航跡の表面に存在する物質が放出されます。 の
得られるヘイズの予測特性については、セクション §2.2 で説明します。

図 5. 曲げ波 (縮尺どおり) とこの作業で使用される 2 つの基準系。 右側のフレームは、
共鳴を中心とし (共鳴時 x = 0)、共回転し、プライムされていない軸 ( ^x, y, ^ z ) によって定義されますが、オイラー
航跡上のフレーム (左上) は、共鳴から距離 r にある自己重力航跡の質量中心の中心にあります。
そしてそれはプライムされた座標 (x^′、ええ』、^z')。 ここでは角度 θq も表します。
' =Rωq'dt ここで ωq' はq の周りの回転の角速度』-軸 ここで q』×でもいい』、y'、またはz』(航跡の主軸)。 の
プライム軸とプライムされていない軸が揃っている場合、角度は 0 になります。

図 13. ヘイズ モデル (表 4 の 3 行目、黒の実線) と SCL モデル (緑の破線、同じパラメータ)
図 12 と同様) (a) β-ケンタウリ (rev77I)、(b) κ-ケンタウリ (rev35E)、(c) α-ヴァージニスの掩蔽 (赤線) と比較
(rev232E)、(d) ϵ-カシオペヤ座 (rev104I)、(e) η-ループス (rev34E)、および (f) κ-おおいぬ座 (rev168I)。 エラーバーは次のとおりです。
プロットの背景に薄赤色の塗りつぶされた曲線として表示されます。 上の行には方位角掩蔽があります
(cos ϕ < 1)、下の行の放射状掩蔽 (cos ϕ > 1)、高、中、低 B 角度 (左から右へ)。
高い Beff 掩蔽の場合、SCL 理論は波全体にわたって不変の光学的深さを予測しますが、代わりに
データは、共鳴から-80kmを中心とした光学的深さの対称的な上昇を示しています。 私たちのモデルは両方を再現します
ピークの位置とガウス様の強調の幅。 ただし、これらのピークの振幅は
私たちのモデルが予測するように、開口角 B によって変化しません。方位角掩蔽の場合、光学式の B によるスケーリング
深度が速すぎるため、モデルは強化のピークを過小予測 (a) し、わずかに過大予測 (c) します。
放射状オカルトでは、スケーリングはうまく機能します。 ヘイズモデルは、
低ベフ掩蔽のデータ。
6. ディスカッション
SCL モデルによって予測された光学的深さとカッシーニ UVIS によって測定された光学的深さの間の相違
および Voyager I (Gresh et al. 1986) は、理論に対する我々の修正によって部分的に対処されました (図12)。 自己重力伴流によって放出されるヘイズ粒子を追加すると、波のプロファイルが変化し、導入部 (§1) の問題 (1) が解決され、可能性が大幅に改善されます (表 4)。 ほとんど
モデルの説明力は、追加の粒子層の存在によってもたらされます。
ただし、図 13 は、観察されたヘイズの光学的深さが方位角輝度非対称性を示していることを示しています。
(ϕ依存性)。 もやは自己重力の後流から来ると仮説を立てていることを考えると(原因は
フラットリングの光学的深さのφ依存性の場合)、観察された異方性はそれらから継承される可能性があります。
この異方性を説明できるようにモデルを改良するには、次の図に示されているダイナミクスをより詳細に分析します。
セクション§2 が必要です。 自己重力航跡が BW 内で優先方向を持ち、ヘイズが存在する場合
前記航跡から生じるヘイズは異方性を示す。 次に、それと比較することができます
動的モデルの追加テストとしての観察。 暫定的に、図 9 は次のことを示唆しています。
方位角方向は優先方向である可能性がありますが、アトラクターを決定するにはさらなる分析が必要です
BW の航跡のローテーションで。
図 12 は、観測された波の減衰長に対するヘイズ モデルの適合により、比較的高い値が得られることを示しています。
動粘度、序論 (§1) の問題 (3) に部分的に対処します。 最適な粘度値
隣接する密度波から得られる粘度の 2 倍以上 (Tiscareno et al. 2007)、Gresh et al. の上部誤差範囲の外に収まります。 (1986) および Esposito ら。 (1983年)。 私たちは自分の価値を比較します
図 14 の文献との比較
図 14. 屈曲波領域付近でさまざまな著者が作成したリングの粘度の測定。
Mimas BW を使用して行われた測定値は 131.9 Mm です。 この論文で計算された値は、
塗りつぶされた三角形。 この研究の値は、より反復的な値 ν = 280 cm2/s よりもかなり高くなります。 私たちの
測定値は Gresh らの誤差範囲の外側にあります。 (1986) および Esposito ら。 (1983) (Tiscareno et al. 2007 および
リサウアーら。 1984 年にはエラーバーは含まれていませんでした)。 エスポジトら。 (1983)、Gresh et al. (1986)、ティスカレノら。 (2007) と
リサウアーら。 (1984) 推定には 1 つの掩蔽 (または画像) を使用していました。 この作業では、60 個のオカルトを使用します。
さまざまなジオメトリ。
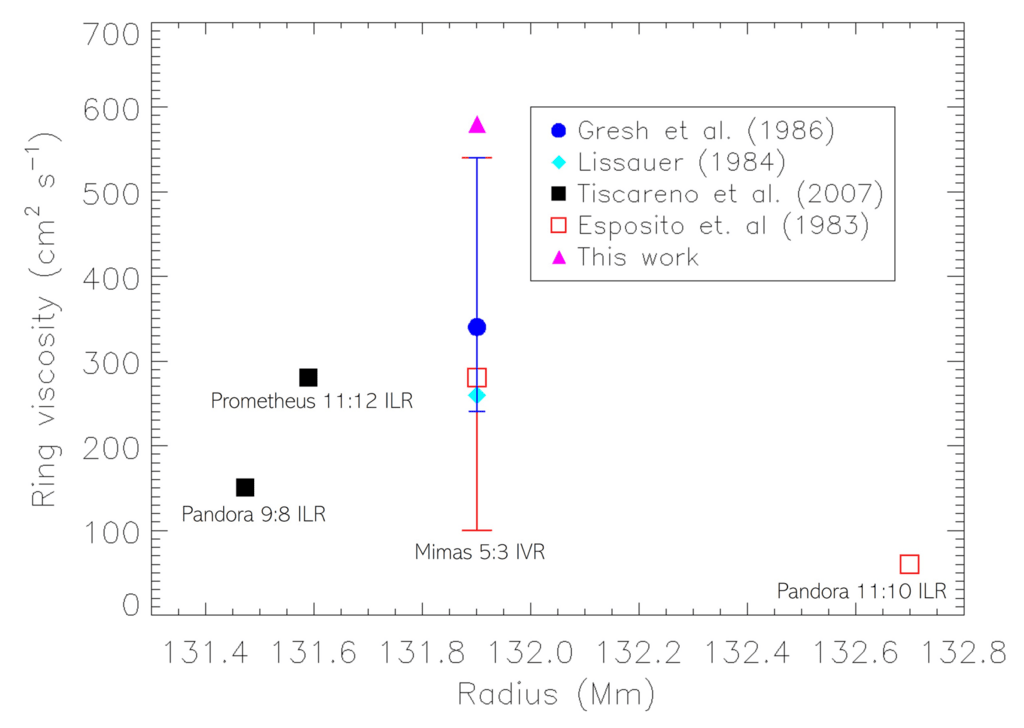
図 14 は、Gresh らの研究結果を示しています。 (1986)、Lissauer et al. (1984)、Esposito et al. (1983) を測定した
私たちの研究で最も適合した値よりも低い粘度。 エスポジトら。 (1983) は δScorpii の 1 つの掩蔽を使用しましたが、Gresh et al. (1986) は、地球の 1 つの低角電波掩蔽 (2 つの周波数) を使用しました。
リサウアーら。 (1984) 隆起リングによって投影される影の画像を使用して、波列がどこにあるかを推定しました。
終了しました。 この研究では、より高い解像度 (400 m 対 2 km) で 60 個の掩蔽を使用します。 信号対雑音比も
γ-ペガサスやβ-ケンタウリなどのより明るい光源を観察しているため、平均してより高くなります。
粘度が低い理由は 2 つあります。 最初のものは、データのノイズと空間解像度に関係します。サイクルが見えなかったため、すべてのサイクルに適合しませんでした。
完全な波列を作成して、減衰長 ξD に適合させようとした粘度を見つけます。これは、次の点です。
波の振幅は e 倍になります。 このアプローチは、SCL 理論が次のような場合に機能します。
この BW には適切ですが、表 4 の最初の行と図 12 に示すように、完全ではないことがわかります。
13. これにより、2 番目の理由、追加の光学深度に対する適切なモデルが存在しないことがわかります。 それなし
ヘイズの粘度の値は、12 のすべてのピークを過小予測します。
グレシュら。 (1986)、掩蔽は非常に低角度であったため、ピークの光学的深さは次のようにみなされました。
無限大(波の傾きと視野角がほぼ同じ)、つまりほぼ一致します。
図 12 では、SCL モデルのフィットにおける不足減衰が確認できます。
谷よりも山の方が顕著です。 要約すると、Gresh et al. (1986)、Lissauer et al. (1984)
およびエスポジトら。 (1983) 粘度値はこの研究で示唆されている値よりも低いです。なぜなら、私たちの掩蔽では波列の後半部分がノイズとその予測から明確に区別できるからです。
減衰長は SCL 理論に依存します。
それにもかかわらず、Gresh et al. の値は次のとおりです。 (1986) この地域で計算された値は、ティスカレノの値よりもまだ高い
他。 (2007) カッシーニ データを使用した 11:12 プロメテウス密度波の分析から計算
は、SCL が適切な弱い曲げ波を調べています (ただし、Tiscareno et al. 2007 は、
プロメテウス 11:12 にはいくつかの非線形性が示されていますが、彼の結果が不正確であると期待するだけでは十分ではありません。
その領域の粘度の他の推定値との一貫性)。 Tiscarenoらと一致するために。
(2007) 次に、BW 自体が密度波と同じように粘度を増加させることを考慮する必要があります。
ない。
問題 (3) にさらに対処するには、航跡の回転に対する波の逆反応を考慮する必要があります。
なぜなら、航跡波相互作用を含めることは、波の減衰長に影響を与えると予想できるからです。
理論。 この追加の散逸を含める方法は、衝突による力の影響を考慮することです (式 1)。
16) 航跡の垂直方向の動きに注意してください。 現在のモデルでは、衝突は南北に発生するとみなされます。
航跡のフレーム内で対称: 同量の粒子が上からと下から航跡に衝突します。
以下では、正味垂直力はゼロになります。 これはおそらく真実ではなく、非弾性航跡波は
衝突は、航跡の垂直運動、および一般にリング粒子の垂直運動の正味の減衰を引き起こすであろう。
この効果を含めていないため、モデルでは高い値を持つことで余分な散逸が考慮されます。
SCL 項の動粘度で、垂直衝突の粘性効果がモデル化されます。
単純に Fvisc/m = νdz/dx ˙ (m は影響を受ける粒子の質量) によって計算されます。 しかし、私たちの単純な
衝突モデルは、傾斜や衝突する質量に依存する、より複雑な相互作用を示唆しています。
自己重力の航跡と航跡のサイズについて。 この粘性力とその後の計算
SCL の波形プロファイルの変更は将来の作業に残されています。
リングと衛星の間の角運動量の保存は、粘性が原因であることを示しています。
というのは、リングの広がりと波を減衰させるものは単純には関係ないかもしれないからである。
(Tajeddine 他、2017)。 ただし、両方の場合の運動量輸送が次の運動によって支配される場合、
自己重力が目覚め、より高い減衰粘度はより効率的な運動量輸送と密接に関係します
その地域では。 次に、ミマス 5:3 の BW は比較的強い (リング内で 2 番目に強い BW) 一方で、自己重力後流により、リングは共鳴時にエネルギーの流入を輸送し、連続波を形成することができます。
この余分な散逸にもかかわらず、ミマス 5:3 BW の傾きは依然として約 15°です。
したがって、次のように推測できます。
自己重力の後流による粘度の増加がなければ、リングに亀裂が入り、
タイタン 0:-1 ノード BW (Nicholson & Hedman 2016) や原始惑星で見られるものと同様のギャップ
円盤は星の傾きに合わせて位置がずれています (Rowther et al. 2022)。 いつ(どの坂で)の理論もなく、
しかし、どの程度の粘性輸送効率で歪んだディスクが壊れるかについては、まだ推測の域を出ません。 アン
カッシーニデータを使用してタイタン 0:-1 ノード BW をモデル化する試みは、リフトの一般理論に光を当てる可能性があります。
円盤に歪みが生じます。
波内のより効率的な角運動量輸送も、拡散を引き起こしている可能性があります。
材料を隣接する領域に送り込みます。 Tiscareno らによって測定された値を考えてみましょう。 (2007)の
プロメテウス 12:11 波の平均表面質量密度。これは土星に比べて約 100 km 近いところにあります。
ミマス 5:3 BW。 平均測定面密度値は σ = 46.1 g/cm2 です。
。 これは以下に対応します
最適な BW 値と比較すると 25% の増加 (Gresh らの値と比較すると 24% の増加)。
1986 年の最適値)。 この密度波の非線形な性質により、密度波の局所的な値が変化する可能性があります。
表面密度 (Borderies et al. 1986) ですが、プロメテウス 12:11 はこの効果が十分に強いわけではありません。
20%以上変更します。 では、なぜこの領域で σ が増加するのでしょうか? 考えられる説明は、密度波は、密度変化現象であるというその性質上、σ の信頼性の低い尺度であるということです。
これでは、測定値が BW 値を過大評価している理由が説明できません。 もう一つのよりもっともらしい
これは、BW 領域の粘度が高いために材料の移動が発生しているためであると考えられます。 地方
粘度の半径方向の増加(減少)は、表面の局所的な減少(増加)に対応することが示されています。
原始惑星系円盤の密度 (Lyra, W. et al. 2015)。 粘度の変化が急激すぎると、
円盤内の渦の成長を刺激する可能性のある不安定性 (Papaloizou & Pringle 1985)。 これがある間、
ここでは当てはまりませんが、屈曲波領域の粘度の増加が表面積の減少を引き起こしている可能性があります。
そこの密度が増加し、それに対応して近くの領域も増加します。
ΦセオリーとΦobsの値を比較すると、波の理論的な位相がほぼ一致していることがわかります。
(表2)。 〜20°の位相差を持つ波が多く存在する中、
、これは予想されることです
半径方向ベクトルまたは共振位置のいずれかにおける半径方向のオフセットが 10 km、誤差が 1 ◦であることで
ミマスの経度は、理論と観測の間で 25°の位相差が生じる可能性があることを意味します。
それにもかかわらず、2 つの星は 90° を超える位相のオフセットを示しています。
: AlpVir(210)I および BetCMa(276)E。 注記
位相のオフセットが補正されると、分散関係はこれらのオカルトに対して適切に機能することがわかります。 それ
これは 40 回の掩蔽のうち 2 回しか起こらないので、提案するのをためらっています。
これほど大きなものを動かすメカニズム
オフセット。 一方、オフセットは、これらの半径方向のオフセットにおけるより大きな系統誤差によるものである可能性があります。
特定の掩蔽。
使用される SCL 分散関係は、波の最初のピークの位置を改善しませんが (導入 §1 の問題 (2))、ほとんどの掩蔽ではかなりうまく機能します (図 13 を参照)。 さらに、
光学的深さのピークのより広い形状により、最初のピークの不一致の一部が部分的に軽減されます。
それにもかかわらず、分散関係が最初の 1 回目だけでなく破綻している 2 つの低角掩蔽が見つかりました。
AlpCMa(274)E と AlpCMa(281)I。 分散関係の差の考えられる原因は、リングの表面質量密度の半径方向の変化である可能性があります。 を使用することで、
等方性モデルの適合値 β = 1.39、方程式 β = Σ0σ ̄ヘイズ (§2.2) を介して、σ ̄ヘイズ = 1 cm2 と仮定します。
最大ヘイズ表面質量密度は 0.4 g/cm2 と推定され、これはリングの最適適合率の約 1% です。
表面質量密度。 したがって、ヘイズの存在は、SCL の分散関係と一致します。
波全体にわたって一定の表面質量密度を仮定しており、それ自体は、波が存在するという証拠ではありません。
リングの密度に大きな変化が見られます。
それにもかかわらず、ヘイズ粒子の平均断面積がより大きい場合 (10 cm、ただし、これは
表 1 が示唆するものとは反対) であり、放射状に変化します (より大きな粒子が放出されるとき、
傾きが大きい) 表面密度に 5 ~ 10% のゆっくりとした半径方向の変化が依然として存在する可能性があり、影響を与える可能性があります。
低ベフ角掩蔽では分散関係が顕著になります。 ウェイクウェーブを組み込むことに注意してください
曲げ波動方程式の相互作用も波の分散関係を変える可能性があります。
共鳴付近の予測波長が改善されます。
ミマス 5:3 BW をより深く理解することで、地球上の他の問題に対処するのに役立ちます。
リング科学。 まず、ミマス 5:3 密度波の説明のつかない高粘度について考えてみましょう (Borderies et al.
1986)。 この粘性の原因は、自己重力伴流の回転にも関連している可能性があります。 ローカル増加
表面密度の変化により、その場所での局所的なせん断速度が低下し、後流がその位置を調整するときに回転する可能性があります。
ピッチ角 (図 7 を参照)。 せん断速度の変化による回転は、従来の回転よりも緩やかになりますが、
この研究で説明されているように、この密度波で見られる局所粘度の増加に寄与する可能性があります。 第二に、
Tiscarenoらによって設定されたパズルを考えてみましょう。 (2013b) Iapetus -1:0 BW 用。 このBWは外側に伝播します
「内側の A リング エッジ」と呼ばれる光学的深さの突然の増加によって。歴史的に、研究者は
は、この光学的深さの増加を表面密度 σ の増加として解釈しました。 ただし、σは波の分散関係にも影響しており、イアペタス -1:0 BWの波長ではそのような急激な変化は見られません。
このエッジが、自己重力がどれほど不安定であるかを考慮して、自己重力が目覚めて形成を開始する点に対応する場合
後流は BW 内の垂直摂動によるものであり、粒子の曇りは光学的傾斜に寄与する可能性があります。
奥行きが増す。 これらの問題に剛体バーとヘイズ モデルを適切に適用することは、今後の作業として残されています。
7. 結論
我々は、剛体自己重力の導入の必然的な結果が線形曲げを引き起こすことを示しました。
波動理論は、屈曲波が振幅に比例する追加の粒子層を生成するというものです。
斜面の。 たとえ、航跡の一部が、
曲げ波、この破壊は依然として同じ層のヘイズ粒子を作成します。
航跡とリングの間の速度は、その特徴的な垂直速度に匹敵します。
波が伝播するにつれて粒子が発生します。
レイ トレーシング コードを使用して、この追加信号をテストしたところ、追加の粒子層が
Shu、Cuzzi、およびCuzziと比較して、BWのカッシーニUVIS掩蔽に対するかなりの説明力
リサウアー (1983)。 私たちの最良のモデルは、ミマス 5:3 の最も矛盾した驚くべき機能を説明しています。
BW; つまり、通常の掩蔽と予想よりも大きな掩蔽の場合の信号の強化です。
粘度、ν = 576 cm2/s、密度波から計算された粘度よりも 2 倍以上大きくなります。 これ
自己重力後流が垂直方向に隙間が開くのを防ぐのに特に効果的であることを示しています。
乱れたディスク。
自己重力後流の剛体バーモデルは、曲げの場合だけでなく成功することが証明されました
波だけでなくフラットリングでも同様です。これは、後流が同じピッチ角で整列する傾向があることを示しています。
相互の自己重力。 したがって、これは、航跡の平均ピッチ角が全体を通して同じである理由を説明できます。
表面質量密度や土星からの距離などのリングの特性が変化しても、A リングと B リングは変化します。
かなりその中にあります。 剛体バーモデルは、動きを調査するための分析ツールとして使用できます。
密度波などの摂動環境では自己重力が目覚めます。
Mimas 5:3 BW の Cassini UVIS データセットの説明は改善されましたが、
現在の屈曲波理論には依然として問題があり、一貫した方法で修正する方法を提案します。
この論文の結果とともに。 理論的な分散関係は最初のサイクルで破綻する傾向があることがわかりました。
場合によっては、波列全体で失敗します。 この理由は、自己重力ウェイクの動きが波の伝播に及ぼす反作用である可能性があります。 この効果を含めることで、
理論をさらに改善するための道として提案されています。
標準的な屈曲波理論 (黒)。 半径131,902kmで共鳴が起こり波が伝播
土星に向かって(プロットの左側)。 3 つの大きな矛盾が見られます: (1) SCL 理論は、ピークを過剰予測します。
光学的深度が低く、谷を過小予測します。 (2) 最初の 3 サイクルでは波長が一致しません。 (3) 理論
ピークはまだ-150 km付近に現れると予測されているため、波が減衰する速度を過小予測していますが、観測された波は
その前にノイズに埋もれてしまいます。 Lissauer らの粘度 ν = 260 cm2/s を使用します。 (1984) の分析
この波とTiscarenoら。 (2007) によるプロメテウス 11:12 密度波の分析。
(3) 粘度。
リングの粘度は、図に見られる光学的深さプロファイルのピークの形状と振幅を制御します。
図 2. 粘性相互作用によりリング粒子の垂直方向の変位が減少します。 それによって、今度は
リングの傾斜と視線が一致する点での最大消光。 言い換えれば、
光学的深さパターンのピーク振幅は粘度に依存します。 図 2 の SCL モデル (黒線)
ピークの多い光学的深さプロファイルと、観察された変動を超えて伝播する波を予測します
データに見られます (赤い線)。 これは、減衰の流体せん断の説明が不十分であること、および/または
以前の Mimas 5:3 BW 研究 (Lissauer et al. 1984; Gresh et al. 1986) および Cassini によって示唆された値
密度波の研究 (Tiscareno et al. 2007) では、この波を説明するには低すぎます。 それにもかかわらず、観察された
光学的深さのピークと波の減衰の速さは、現在の理論が波の領域に拡散するエネルギーと運動量の量を過小予測していることを示しています。 この拡散の欠落は、次の原因によって引き起こされる可能性があります。
図 3 で示唆されている追加の粒子層を生成するメカニズムと同じです。
3 つの問題はすべて、カッシーニのリング掩蔽データを使用して詳しく調べることができます。 カッシーニがミマ星を観測
UVIS 高速光度計 (HSP) (Esposito et al. 2004) を使用した 217 回の掩蔽で 5:3 BW
これら 130 は、屈曲波によるデータの変化を検出するのに十分な高い S/N 比を持っています。
さらに、Cassini データを使用して、Colwell et al. (2006) は自己重力航跡の存在を確認しました。
周期的に凝集し、典型的な A 粒子よりも 10 ~ 100 倍大きい粒子の細長い塊。
リング粒子(〜 1 m)(Jerousek et al. 2016; Salo et al. 2018)。 自己重力覚醒を追加した結果
SCL 理論への影響は、関連するトルクに剛体として反応するという仮定を介してセクション 2 で導き出されます。
天体。 ここで我々は、通常の掩蔽で見られる追加の光学的深度信号を説明するメカニズムを提示します。
セクション §3 では、透過モデル、使用される 60 個の UVIS 掩蔽の選択基準について説明します。
データがどのように削減されたか。 セクション §4 では、レイ トレーシング コードについて説明します。 セクション §5 で比較します。
屈曲波モデルをデータに当てはめた後、セクション 6 で説明します。
このモデルは上記の問題を解決します。 セクション §7 で結論を要約します。

図 3. 左のパネル: β-ケンタウリの掩蔽を比較します (rev85I、B = 66.7◦、ベフ = 87°) (赤く点灯)、
SCLモデル(ソリッドバック)。 エラーバーは、プロットの背景に薄赤色の塗りつぶされた曲線として表示されます。 の
SCL 理論は均一な光学的深さを予測します。 ただし、データは、中心を中心とした光学的深さの対称的な上昇を示しています。
共鳴から−80km。 右パネル: β-Centauri の同じ光学深度プロファイル (赤色の実線) が、β-Centauri の光学深度プロファイルと比較されています。
理論的 (SCL 理論) の波の最大傾き (黒の実線) と波の振幅 (青の破線)
粘度 566 cm2/s、リング表面密度 σ = 36.3 g/cm2; これらの値は、この論文で紹介されているモデル。

図 4. シアーシート REBOUND の例で生成されたシアーボックス シミュレーションにおける自己重力ウェイクのスナップショット
(Rein & Liu 2012)、視覚化のみを目的としています。 赤で囲まれた部分には、指向性のある自己重力の航跡が見られます。 我々はできる
また、それらは方位角に対して角度 θw を指す傾向があることもわかります。
2. 自己重力後流と屈曲波
自己重力後流は、方位角から角度 θw の細長い構造を持つ粒子の塊です。
これらは、ケプラーせん断に抗して自己重力によって一緒に保持されます (図 4 を参照)。
構成粒子は、相対距離の変更に対する抵抗を示します (Δrij ≈ 0) (Daisaka & Ida 1999;ルーら。 2018)。
言い換えれば、航跡内の粒子は一貫した動きを示し、航跡は一定の速度を維持します。
1 軌道周期の時間スケールでの形状と方向の一貫性 (Karjalainen & Salo 2004)。 自己重力
航跡は、銀河系の文脈で非軸対称の擾乱として初めて仮説が立てられました (Toomre 1964)。
回転ディスクの自己重力とそのせん断の相互作用によって生成されます。 彼らが最初に提案したのは、
Colombo et al. によるリングに存在します。 (1976)、および Dones & Porco (1989)、および Dunn et al. (2004) は、ボイジャー画像と超大型アレイ観測に対するそれらの影響をそれぞれモデル化し、裏付けました。 彼らはいた
惑星環はサロ (1992) によって初めて数値モデル化され、コルウェルの土星の環で検出されました。
他。 (2006) UVIS 掩蔽の光学的深さにおける方位角の非対称性として。
SCL 線形屈曲波理論では、リングが滑らかで密度が均一であるとみなします。
これらの構造は力学では考慮されていませんでした。 自己重力覚醒の影響を研究するために、
少なくとも波が波内で 1 波長進むのにかかる時間の間は、それらは堅いままであると仮定します。
フレームは航跡と共回転し、これは約 1 軌道周期です (以下の式 5 を参照)。 少なくとも一部の自己重力航跡は、その期間にわたって一緒に留まることが予想されます (Karjalainen & Salo 2004): シミュレーションでも
多くの軌道周期の可能性のある寿命を示唆しています (Michibashi et al. 2015)。
BW 内では、後流は方向 (θq) に影響を与えるさまざまなトルクを受けます。
'、図 5 を参照)
波に合わせて高度 (z) に振動します。 これらのトルクとその回転運動への影響
航跡はセクション §2.1 で計算されます。 航跡が方向を変えるにつれて、航跡が
後流の中心からある程度の距離にある粒子は、後流との垂直速度に差が生じます。
周囲のリング粒子 (予想される SCL の垂直方向の動きに従うと想定されます)、その結果、
相対速度が 1 cm/s 程度の衝突で、航跡の表面に存在する物質が放出されます。 の
得られるヘイズの予測特性については、セクション §2.2 で説明します。

図 5. 曲げ波 (縮尺どおり) とこの作業で使用される 2 つの基準系。 右側のフレームは、
共鳴を中心とし (共鳴時 x = 0)、共回転し、プライムされていない軸 ( ^x, y, ^ z ) によって定義されますが、オイラー
航跡上のフレーム (左上) は、共鳴から距離 r にある自己重力航跡の質量中心の中心にあります。
そしてそれはプライムされた座標 (x^′、ええ』、^z')。 ここでは角度 θq も表します。
' =Rωq'dt ここで ωq' はq の周りの回転の角速度』-軸 ここで q』×でもいい』、y'、またはz』(航跡の主軸)。 の
プライム軸とプライムされていない軸が揃っている場合、角度は 0 になります。

図 13. ヘイズ モデル (表 4 の 3 行目、黒の実線) と SCL モデル (緑の破線、同じパラメータ)
図 12 と同様) (a) β-ケンタウリ (rev77I)、(b) κ-ケンタウリ (rev35E)、(c) α-ヴァージニスの掩蔽 (赤線) と比較
(rev232E)、(d) ϵ-カシオペヤ座 (rev104I)、(e) η-ループス (rev34E)、および (f) κ-おおいぬ座 (rev168I)。 エラーバーは次のとおりです。
プロットの背景に薄赤色の塗りつぶされた曲線として表示されます。 上の行には方位角掩蔽があります
(cos ϕ < 1)、下の行の放射状掩蔽 (cos ϕ > 1)、高、中、低 B 角度 (左から右へ)。
高い Beff 掩蔽の場合、SCL 理論は波全体にわたって不変の光学的深さを予測しますが、代わりに
データは、共鳴から-80kmを中心とした光学的深さの対称的な上昇を示しています。 私たちのモデルは両方を再現します
ピークの位置とガウス様の強調の幅。 ただし、これらのピークの振幅は
私たちのモデルが予測するように、開口角 B によって変化しません。方位角掩蔽の場合、光学式の B によるスケーリング
深度が速すぎるため、モデルは強化のピークを過小予測 (a) し、わずかに過大予測 (c) します。
放射状オカルトでは、スケーリングはうまく機能します。 ヘイズモデルは、
低ベフ掩蔽のデータ。
6. ディスカッション
SCL モデルによって予測された光学的深さとカッシーニ UVIS によって測定された光学的深さの間の相違
および Voyager I (Gresh et al. 1986) は、理論に対する我々の修正によって部分的に対処されました (図12)。 自己重力伴流によって放出されるヘイズ粒子を追加すると、波のプロファイルが変化し、導入部 (§1) の問題 (1) が解決され、可能性が大幅に改善されます (表 4)。 ほとんど
モデルの説明力は、追加の粒子層の存在によってもたらされます。
ただし、図 13 は、観察されたヘイズの光学的深さが方位角輝度非対称性を示していることを示しています。
(ϕ依存性)。 もやは自己重力の後流から来ると仮説を立てていることを考えると(原因は
フラットリングの光学的深さのφ依存性の場合)、観察された異方性はそれらから継承される可能性があります。
この異方性を説明できるようにモデルを改良するには、次の図に示されているダイナミクスをより詳細に分析します。
セクション§2 が必要です。 自己重力航跡が BW 内で優先方向を持ち、ヘイズが存在する場合
前記航跡から生じるヘイズは異方性を示す。 次に、それと比較することができます
動的モデルの追加テストとしての観察。 暫定的に、図 9 は次のことを示唆しています。
方位角方向は優先方向である可能性がありますが、アトラクターを決定するにはさらなる分析が必要です
BW の航跡のローテーションで。
図 12 は、観測された波の減衰長に対するヘイズ モデルの適合により、比較的高い値が得られることを示しています。
動粘度、序論 (§1) の問題 (3) に部分的に対処します。 最適な粘度値
隣接する密度波から得られる粘度の 2 倍以上 (Tiscareno et al. 2007)、Gresh et al. の上部誤差範囲の外に収まります。 (1986) および Esposito ら。 (1983年)。 私たちは自分の価値を比較します
図 14 の文献との比較
図 14. 屈曲波領域付近でさまざまな著者が作成したリングの粘度の測定。
Mimas BW を使用して行われた測定値は 131.9 Mm です。 この論文で計算された値は、
塗りつぶされた三角形。 この研究の値は、より反復的な値 ν = 280 cm2/s よりもかなり高くなります。 私たちの
測定値は Gresh らの誤差範囲の外側にあります。 (1986) および Esposito ら。 (1983) (Tiscareno et al. 2007 および
リサウアーら。 1984 年にはエラーバーは含まれていませんでした)。 エスポジトら。 (1983)、Gresh et al. (1986)、ティスカレノら。 (2007) と
リサウアーら。 (1984) 推定には 1 つの掩蔽 (または画像) を使用していました。 この作業では、60 個のオカルトを使用します。
さまざまなジオメトリ。

図 14 は、Gresh らの研究結果を示しています。 (1986)、Lissauer et al. (1984)、Esposito et al. (1983) を測定した
私たちの研究で最も適合した値よりも低い粘度。 エスポジトら。 (1983) は δScorpii の 1 つの掩蔽を使用しましたが、Gresh et al. (1986) は、地球の 1 つの低角電波掩蔽 (2 つの周波数) を使用しました。
リサウアーら。 (1984) 隆起リングによって投影される影の画像を使用して、波列がどこにあるかを推定しました。
終了しました。 この研究では、より高い解像度 (400 m 対 2 km) で 60 個の掩蔽を使用します。 信号対雑音比も
γ-ペガサスやβ-ケンタウリなどのより明るい光源を観察しているため、平均してより高くなります。
粘度が低い理由は 2 つあります。 最初のものは、データのノイズと空間解像度に関係します。サイクルが見えなかったため、すべてのサイクルに適合しませんでした。
完全な波列を作成して、減衰長 ξD に適合させようとした粘度を見つけます。これは、次の点です。
波の振幅は e 倍になります。 このアプローチは、SCL 理論が次のような場合に機能します。
この BW には適切ですが、表 4 の最初の行と図 12 に示すように、完全ではないことがわかります。
13. これにより、2 番目の理由、追加の光学深度に対する適切なモデルが存在しないことがわかります。 それなし
ヘイズの粘度の値は、12 のすべてのピークを過小予測します。
グレシュら。 (1986)、掩蔽は非常に低角度であったため、ピークの光学的深さは次のようにみなされました。
無限大(波の傾きと視野角がほぼ同じ)、つまりほぼ一致します。
図 12 では、SCL モデルのフィットにおける不足減衰が確認できます。
谷よりも山の方が顕著です。 要約すると、Gresh et al. (1986)、Lissauer et al. (1984)
およびエスポジトら。 (1983) 粘度値はこの研究で示唆されている値よりも低いです。なぜなら、私たちの掩蔽では波列の後半部分がノイズとその予測から明確に区別できるからです。
減衰長は SCL 理論に依存します。
それにもかかわらず、Gresh et al. の値は次のとおりです。 (1986) この地域で計算された値は、ティスカレノの値よりもまだ高い
他。 (2007) カッシーニ データを使用した 11:12 プロメテウス密度波の分析から計算
は、SCL が適切な弱い曲げ波を調べています (ただし、Tiscareno et al. 2007 は、
プロメテウス 11:12 にはいくつかの非線形性が示されていますが、彼の結果が不正確であると期待するだけでは十分ではありません。
その領域の粘度の他の推定値との一貫性)。 Tiscarenoらと一致するために。
(2007) 次に、BW 自体が密度波と同じように粘度を増加させることを考慮する必要があります。
ない。
問題 (3) にさらに対処するには、航跡の回転に対する波の逆反応を考慮する必要があります。
なぜなら、航跡波相互作用を含めることは、波の減衰長に影響を与えると予想できるからです。
理論。 この追加の散逸を含める方法は、衝突による力の影響を考慮することです (式 1)。
16) 航跡の垂直方向の動きに注意してください。 現在のモデルでは、衝突は南北に発生するとみなされます。
航跡のフレーム内で対称: 同量の粒子が上からと下から航跡に衝突します。
以下では、正味垂直力はゼロになります。 これはおそらく真実ではなく、非弾性航跡波は
衝突は、航跡の垂直運動、および一般にリング粒子の垂直運動の正味の減衰を引き起こすであろう。
この効果を含めていないため、モデルでは高い値を持つことで余分な散逸が考慮されます。
SCL 項の動粘度で、垂直衝突の粘性効果がモデル化されます。
単純に Fvisc/m = νdz/dx ˙ (m は影響を受ける粒子の質量) によって計算されます。 しかし、私たちの単純な
衝突モデルは、傾斜や衝突する質量に依存する、より複雑な相互作用を示唆しています。
自己重力の航跡と航跡のサイズについて。 この粘性力とその後の計算
SCL の波形プロファイルの変更は将来の作業に残されています。
リングと衛星の間の角運動量の保存は、粘性が原因であることを示しています。
というのは、リングの広がりと波を減衰させるものは単純には関係ないかもしれないからである。
(Tajeddine 他、2017)。 ただし、両方の場合の運動量輸送が次の運動によって支配される場合、
自己重力が目覚め、より高い減衰粘度はより効率的な運動量輸送と密接に関係します
その地域では。 次に、ミマス 5:3 の BW は比較的強い (リング内で 2 番目に強い BW) 一方で、自己重力後流により、リングは共鳴時にエネルギーの流入を輸送し、連続波を形成することができます。
この余分な散逸にもかかわらず、ミマス 5:3 BW の傾きは依然として約 15°です。
したがって、次のように推測できます。
自己重力の後流による粘度の増加がなければ、リングに亀裂が入り、
タイタン 0:-1 ノード BW (Nicholson & Hedman 2016) や原始惑星で見られるものと同様のギャップ
円盤は星の傾きに合わせて位置がずれています (Rowther et al. 2022)。 いつ(どの坂で)の理論もなく、
しかし、どの程度の粘性輸送効率で歪んだディスクが壊れるかについては、まだ推測の域を出ません。 アン
カッシーニデータを使用してタイタン 0:-1 ノード BW をモデル化する試みは、リフトの一般理論に光を当てる可能性があります。
円盤に歪みが生じます。
波内のより効率的な角運動量輸送も、拡散を引き起こしている可能性があります。
材料を隣接する領域に送り込みます。 Tiscareno らによって測定された値を考えてみましょう。 (2007)の
プロメテウス 12:11 波の平均表面質量密度。これは土星に比べて約 100 km 近いところにあります。
ミマス 5:3 BW。 平均測定面密度値は σ = 46.1 g/cm2 です。
。 これは以下に対応します
最適な BW 値と比較すると 25% の増加 (Gresh らの値と比較すると 24% の増加)。
1986 年の最適値)。 この密度波の非線形な性質により、密度波の局所的な値が変化する可能性があります。
表面密度 (Borderies et al. 1986) ですが、プロメテウス 12:11 はこの効果が十分に強いわけではありません。
20%以上変更します。 では、なぜこの領域で σ が増加するのでしょうか? 考えられる説明は、密度波は、密度変化現象であるというその性質上、σ の信頼性の低い尺度であるということです。
これでは、測定値が BW 値を過大評価している理由が説明できません。 もう一つのよりもっともらしい
これは、BW 領域の粘度が高いために材料の移動が発生しているためであると考えられます。 地方
粘度の半径方向の増加(減少)は、表面の局所的な減少(増加)に対応することが示されています。
原始惑星系円盤の密度 (Lyra, W. et al. 2015)。 粘度の変化が急激すぎると、
円盤内の渦の成長を刺激する可能性のある不安定性 (Papaloizou & Pringle 1985)。 これがある間、
ここでは当てはまりませんが、屈曲波領域の粘度の増加が表面積の減少を引き起こしている可能性があります。
そこの密度が増加し、それに対応して近くの領域も増加します。
ΦセオリーとΦobsの値を比較すると、波の理論的な位相がほぼ一致していることがわかります。
(表2)。 〜20°の位相差を持つ波が多く存在する中、
、これは予想されることです
半径方向ベクトルまたは共振位置のいずれかにおける半径方向のオフセットが 10 km、誤差が 1 ◦であることで
ミマスの経度は、理論と観測の間で 25°の位相差が生じる可能性があることを意味します。
それにもかかわらず、2 つの星は 90° を超える位相のオフセットを示しています。
: AlpVir(210)I および BetCMa(276)E。 注記
位相のオフセットが補正されると、分散関係はこれらのオカルトに対して適切に機能することがわかります。 それ
これは 40 回の掩蔽のうち 2 回しか起こらないので、提案するのをためらっています。
これほど大きなものを動かすメカニズム
オフセット。 一方、オフセットは、これらの半径方向のオフセットにおけるより大きな系統誤差によるものである可能性があります。
特定の掩蔽。
使用される SCL 分散関係は、波の最初のピークの位置を改善しませんが (導入 §1 の問題 (2))、ほとんどの掩蔽ではかなりうまく機能します (図 13 を参照)。 さらに、
光学的深さのピークのより広い形状により、最初のピークの不一致の一部が部分的に軽減されます。
それにもかかわらず、分散関係が最初の 1 回目だけでなく破綻している 2 つの低角掩蔽が見つかりました。
AlpCMa(274)E と AlpCMa(281)I。 分散関係の差の考えられる原因は、リングの表面質量密度の半径方向の変化である可能性があります。 を使用することで、
等方性モデルの適合値 β = 1.39、方程式 β = Σ0σ ̄ヘイズ (§2.2) を介して、σ ̄ヘイズ = 1 cm2 と仮定します。
最大ヘイズ表面質量密度は 0.4 g/cm2 と推定され、これはリングの最適適合率の約 1% です。
表面質量密度。 したがって、ヘイズの存在は、SCL の分散関係と一致します。
波全体にわたって一定の表面質量密度を仮定しており、それ自体は、波が存在するという証拠ではありません。
リングの密度に大きな変化が見られます。
それにもかかわらず、ヘイズ粒子の平均断面積がより大きい場合 (10 cm、ただし、これは
表 1 が示唆するものとは反対) であり、放射状に変化します (より大きな粒子が放出されるとき、
傾きが大きい) 表面密度に 5 ~ 10% のゆっくりとした半径方向の変化が依然として存在する可能性があり、影響を与える可能性があります。
低ベフ角掩蔽では分散関係が顕著になります。 ウェイクウェーブを組み込むことに注意してください
曲げ波動方程式の相互作用も波の分散関係を変える可能性があります。
共鳴付近の予測波長が改善されます。
ミマス 5:3 BW をより深く理解することで、地球上の他の問題に対処するのに役立ちます。
リング科学。 まず、ミマス 5:3 密度波の説明のつかない高粘度について考えてみましょう (Borderies et al.
1986)。 この粘性の原因は、自己重力伴流の回転にも関連している可能性があります。 ローカル増加
表面密度の変化により、その場所での局所的なせん断速度が低下し、後流がその位置を調整するときに回転する可能性があります。
ピッチ角 (図 7 を参照)。 せん断速度の変化による回転は、従来の回転よりも緩やかになりますが、
この研究で説明されているように、この密度波で見られる局所粘度の増加に寄与する可能性があります。 第二に、
Tiscarenoらによって設定されたパズルを考えてみましょう。 (2013b) Iapetus -1:0 BW 用。 このBWは外側に伝播します
「内側の A リング エッジ」と呼ばれる光学的深さの突然の増加によって。歴史的に、研究者は
は、この光学的深さの増加を表面密度 σ の増加として解釈しました。 ただし、σは波の分散関係にも影響しており、イアペタス -1:0 BWの波長ではそのような急激な変化は見られません。
このエッジが、自己重力がどれほど不安定であるかを考慮して、自己重力が目覚めて形成を開始する点に対応する場合
後流は BW 内の垂直摂動によるものであり、粒子の曇りは光学的傾斜に寄与する可能性があります。
奥行きが増す。 これらの問題に剛体バーとヘイズ モデルを適切に適用することは、今後の作業として残されています。
7. 結論
我々は、剛体自己重力の導入の必然的な結果が線形曲げを引き起こすことを示しました。
波動理論は、屈曲波が振幅に比例する追加の粒子層を生成するというものです。
斜面の。 たとえ、航跡の一部が、
曲げ波、この破壊は依然として同じ層のヘイズ粒子を作成します。
航跡とリングの間の速度は、その特徴的な垂直速度に匹敵します。
波が伝播するにつれて粒子が発生します。
レイ トレーシング コードを使用して、この追加信号をテストしたところ、追加の粒子層が
Shu、Cuzzi、およびCuzziと比較して、BWのカッシーニUVIS掩蔽に対するかなりの説明力
リサウアー (1983)。 私たちの最良のモデルは、ミマス 5:3 の最も矛盾した驚くべき機能を説明しています。
BW; つまり、通常の掩蔽と予想よりも大きな掩蔽の場合の信号の強化です。
粘度、ν = 576 cm2/s、密度波から計算された粘度よりも 2 倍以上大きくなります。 これ
自己重力後流が垂直方向に隙間が開くのを防ぐのに特に効果的であることを示しています。
乱れたディスク。
自己重力後流の剛体バーモデルは、曲げの場合だけでなく成功することが証明されました
波だけでなくフラットリングでも同様です。これは、後流が同じピッチ角で整列する傾向があることを示しています。
相互の自己重力。 したがって、これは、航跡の平均ピッチ角が全体を通して同じである理由を説明できます。
表面質量密度や土星からの距離などのリングの特性が変化しても、A リングと B リングは変化します。
かなりその中にあります。 剛体バーモデルは、動きを調査するための分析ツールとして使用できます。
密度波などの摂動環境では自己重力が目覚めます。
Mimas 5:3 BW の Cassini UVIS データセットの説明は改善されましたが、
現在の屈曲波理論には依然として問題があり、一貫した方法で修正する方法を提案します。
この論文の結果とともに。 理論的な分散関係は最初のサイクルで破綻する傾向があることがわかりました。
場合によっては、波列全体で失敗します。 この理由は、自己重力ウェイクの動きが波の伝播に及ぼす反作用である可能性があります。 この効果を含めることで、
理論をさらに改善するための道として提案されています。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます