天王星を傾ける：衝突対自転公転共鳴

天王星の自転軸が傾いてるのは地球質量の原始惑星が衝突した説に異を唱えるマイグレーションによる自転公転共鳴で傾いた説です。９８度全ては傾けられないので衝突と共鳴のハイブリッド説です。以下、機械翻訳。
天王星を傾ける：衝突対自転公転共鳴
2020年4月30日に提出
この論文では、惑星の起源が太陽に近いと仮定して、天王星の98°傾斜が永年の自転公転共鳴の副産物であったかどうかを調査します。この位置では、天王星のスピン歳差運動周波数は土星の向こうにある別の惑星と共鳴するのに十分な速さです。数値積分を使用して、過去のさまざまな太陽系構成で共鳴捕獲が可能であることを示しますが、惑星を90°オーダーに傾斜させるのに必要なタイムスケールは〜10＾8年です。不快に長いタイムスパン。条件が理想的である場合、共鳴キックは～ 10 ^7年で惑星をかなりの40°に傾ける可能性があります。
また、天王星の大きな傾斜の起源に関する衝突仮説を再検討します。インパクターから与えられた角運動量を合計して惑星を構築する新しい衝突コードを使用して、複数の影響を検討します。ガス降着は惑星の回転角運動量の未知の、しかしおそらく大きな部分を与えるので、傾斜した、傾いた、回転している、および回転していない惑星の異なる衝突モデルを比較します。惑星の現在のスピン状態を説明するには、合計で1 M ⊕の 2つの衝突で十分であることがわかります 。最後に、ハイブリッドモデルを調査し、衝突モデルの顕著な改善のために、共鳴により〜 40° の傾斜が生じる必要があることを示します。

図1.天王星の自転軸を表す3つの量の計算された相対誤差。 ここで、ωは単位です
天王星の回転軸の方向を指すベクトル。 は惑星の傾斜であり、φは惑星の回転です
昇順ノードの経度。 システムに含まれるのはすべてであるため、すべての量は時間とともに一定でなければなりません
太陽と天王星。 ここに示されているレベルの数値誤差は、目的に応じて十分に低くなっています。


図2.レゾナンスキャプチャ。 上部のパネルは、天王星の傾斜の経時変化を示しています。 真ん中
パネルは、共振位置を示す破線で歳差周波数の変化を示しています。
下部のパネルには、共振角度（Ψ）が表示されます。 t≈150 Myrの垂直の実線は、
海王星は現在の場所に30 auで到達します。 このシミュレーションでは、t = 0.05 Gyrで共振が確立されます。
ネプチューンが≈24 auであり、t = 0.85 auで壊れ、ネプチューンが≈120 auである。 海王星の停止
30 auでは、この捕獲が天王星の極端な傾斜のおそらく半分を占める可能性があることがわかりました。 ここ、天王星
現在の赤道半径で、aU = 7 auにあります。 海王星の傾きは現在の2倍に設定されています　共振を強化するiN = 4°での値。


図3.図2に対応する極座標プロット。海王星は断熱的にうまく移動しています。
限定。 ここでの短い周期の振動は極の歳差運動率であり、長い振動は
それ自体がより高い傾斜（右）に移動している平衡点に関する平衡。 赤い点線の円は、一定の傾斜のポイントを15°の増分で表します。


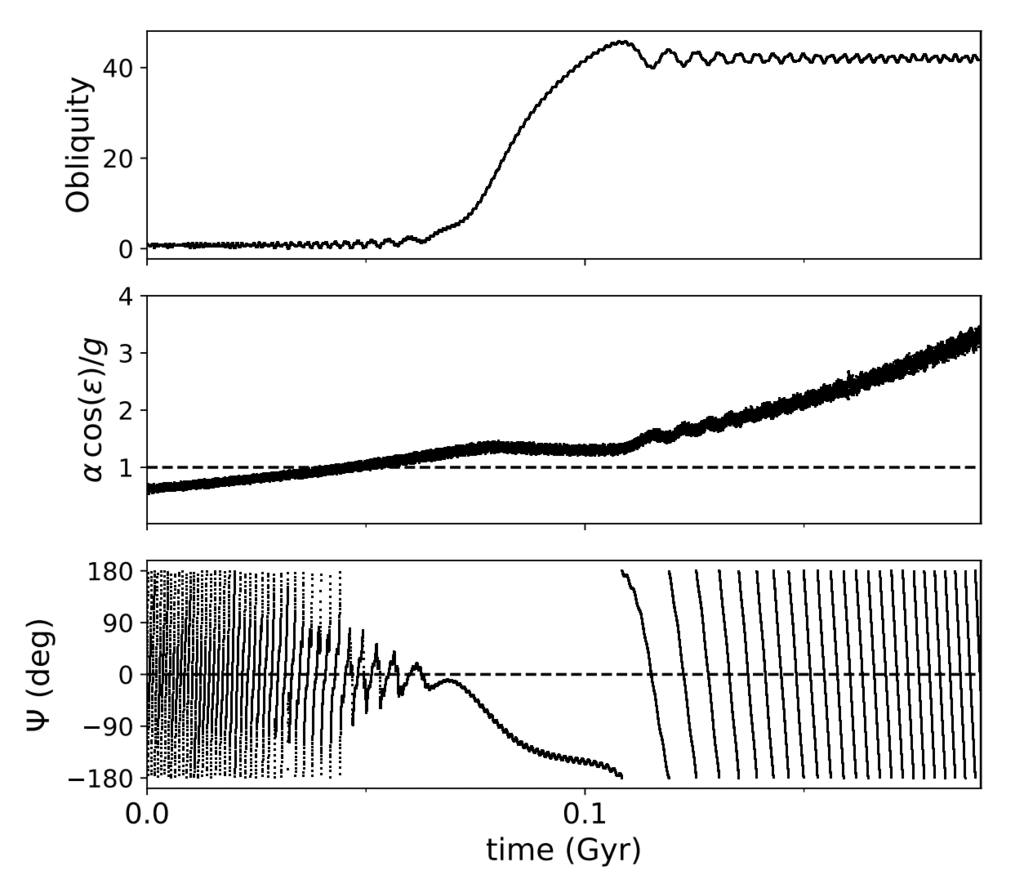
図4.振幅が特に大きい40°のレゾナンスキック。 ここで海王星は急速に移住しています
平均速度は0.068 au / Myrで、天王星の半径は現在のサイズです。 木星、土星、天王星現在より10％太陽に近い位置にあり、海王星は4°の傾きを持っています。


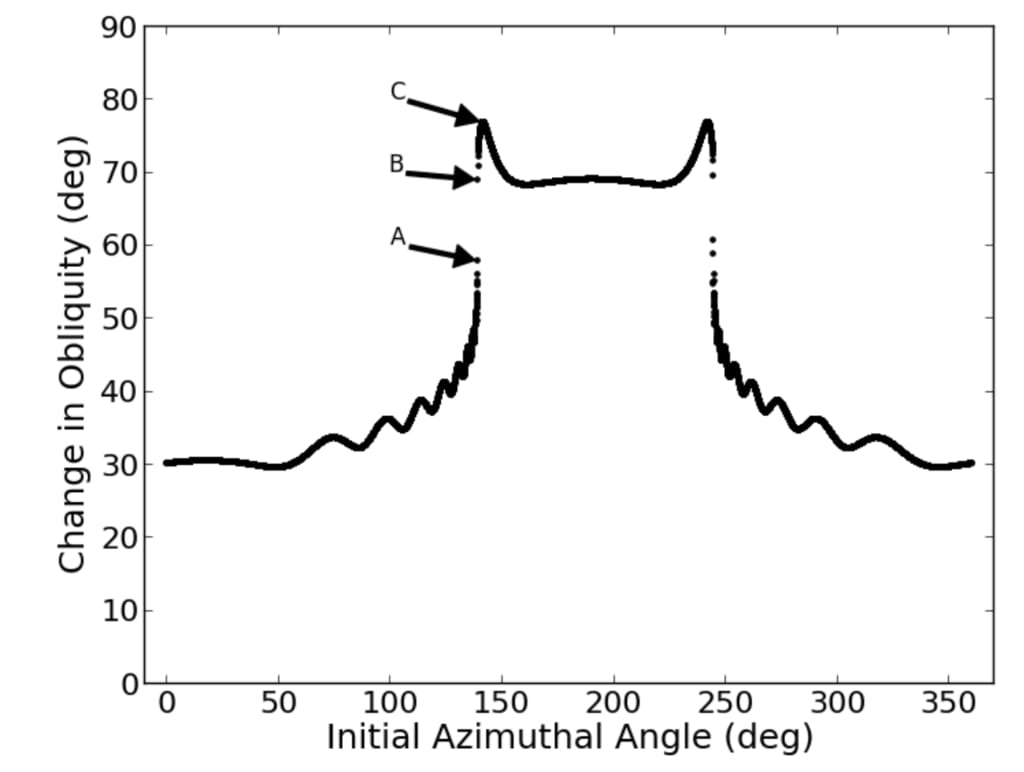
図5.この図は、天王星の初期方位角の関数としての傾斜の変化を示しています。
= 1°、iN = 8°、システムは断熱限界に近い。 ここでは、10,000の初期方位角をサンプリングしました
0°から360°に傾斜を上げ、キックからの移行領域（フェーズキャプチャ（0°付近の位相）に0°付近）。 注釈付きポイント（A、B、C）については、図6で詳しく説明します。


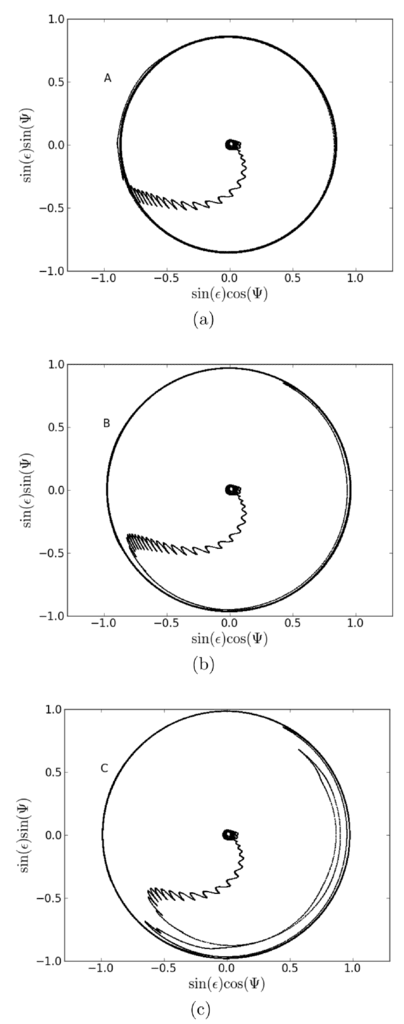
図6.これらは、図5から取られた1つのキック（a）と2つのキャプチャ（b、c）の極座標プロットです。
図5の遷移領域での共振キック。共振角は1回未満の変動を受ける
サイクル。 180°に近づき、共振を残します。 B：非常に希薄な捕獲。
共鳴を逃れる前に数サイクルの間180°を超え、大きな外側の円を作ります。 C：共鳴
図5のキャプチャ領域内で十分にキャプチャします。ここでも、システムは共振から解放されます
数回の解放サイクルの後。 これらのプロットの短周期振動は、極の歳差運動の影響によるものです。


図7.この図は、初期の範囲のキャプチャを生成する共振の割合を示しています
不確実性と移行速度。 キャプチャは図の左下隅で最も簡単に発生します　不確実性と遅い移行率。 ここではiN = 4°です。