ウェルカムの精神

レインボーシックスシージのフロストのウェルカムマットをマイクラの地図絵で作った
設計図はMinecraft Dotを使用
材料集めも整地も設置も自力でやったので相当時間かかった

でも実際にトラップとして使うのは難しい
感圧板の上に置くと浮いてしまうし、ジョーク的インテリアにしかならない
優しい世界

進捗コンプリート

最後の進捗はシュルカーで50ブロック浮上のやつ
長い道のりだった



一番苦労したのはパンダの交配
近場のどのジャングルにも1匹しかいなくて、仕方なくネザー経由で運ぼうとした
1500ブロックほどレールつなげていざ運んだら、トロッコが壁に接するときの窒息ダメージでパンダが死んだ…
結局2匹いるジャングルが見つかるまでひたすら飛ぶハメに
これSeed Map使わなかったら不可能に思える



ガストをオーバーワールドに持ってくるのもひたすら時間がかかった
ネザーでたわむれてたら達成できたので大変さはあんまりない



トライデントが全然取れなくてドラウンドトラップを作った
作って稼働したらすぐに出て複雑な気分
デザインで建材の不足が丸わかり
こういう建築で土使う人初めて見た


実績解除ゲーとしてのマイクラはかなり楽しめた
ダイヤ装備作ってからは全ロスもなく、エリトラの操作もお手のもの
理解がずいぶんと深まった

隠し進捗の方は、今日はやめておきます

真面目にマイクラをやる時期

片手間に始めたら止まらなくなった
ちゃんとプレイするとわりと難易度が高くて驚き
新しいネザーで鉄装備の弱さを思い知らされた



適当にかまえた拠点のすぐそばにゾンスポという好条件
経験値よりもゾンビをいつでも調達できる便利さが至高



家は豆腐で間仕切りもろくにしてない
おしゃれ建築をするには時期が悪い



今の仕事は司書ガチャ
全ロス対策のために入念な環境整備が必要であります
一張羅のダイヤでエンドに突入とかネザーで残骸探索だとか
そういう勇気はHIPのYOU

マインクラフトで遺跡を３つとも見つけよう

みっつけよう('ｍ`)

と思っていろいろ計算してみたんですけど
結論から言ってできませんでした


遺跡（要塞）のまとめ
・１つのワールドに３つ存在する
・元の地点から半径640～1152ブロックの範囲内のランダムな場所にある
・３つの遺跡は、ワールドの中心からみてほぼ同じ角度の間隔にある
　（つまり原点から見て他の遺跡から120°の場所にある）


まずやったのは、
遺跡が３つとも原点から等距離だと仮定して、それぞれの座標を求めてみた
実際は等距離じゃなくてバラバラなんだけど、周辺を掘ればすぐ見つかると思った

出た計算式がこちら（導出は大変だったので省略）

　１つ目の遺跡の座標を (x, z)=(s, t) とすると
　遺跡２　(x, z)=(-0.5s+0.866t, -0.5t-0.866s)
　遺跡３　(x, z)=(-0.5s-0.866t, -0.5t+0.866s)　　　　　　　　　　　　※0.866ってのは√3/2

例えば１つ目の座標が (-110, -615) の場合は
遺跡２　(-478, 403)
遺跡３　(588, 212)
となる

これを元に捜索したところ、実際は以下の場所にありました
遺跡２　(-768, 595)
遺跡３　(741, 368)

原点からの距離がバラバラなんだから違って当たり前なんですけど
問題はそこじゃなかった


３つの遺跡が原点から見て120°で等間隔に存在する、というのが　「大体」　ってことが判明した


上の座標からそれぞれの遺跡の角度を出してみたら
遺跡１－２間　117.6°
遺跡２－３間　115.8°
遺跡３－１間　126.6°

ずれまくり！
どうりで全然違う方向にあったわけ

何かの間違いかと思い、他の方が上げてる遺跡の座標でも計算してみた
　遺跡１　(-872, 108)　　遺跡２　(518, -618)　　遺跡３　(395, 722)
この場合だと
遺跡１－２間　137.0°
遺跡２－３間　111.6°
遺跡３－１間　111.3°

もうなにもあてにならない・・・


距離がランダムで角度も適当なので、結局手探りで探すしかないです
エンダーアイがどうやら一番近い遺跡に反応するっぽいので
投げまくって探してください( ˘ω˘)


原点は0,0じゃないんじゃないか？なんて疑問も沸いてくる
すごく時間を無駄にした試みだった

マインクラフトで遺跡の場所を割り出そう

離れた2カ所でエンダーパールを投げて、
その座標と方角から遺跡（要塞）の場所を特定しようと思った
計算式が見つからないからここにメモ

理屈は単純
2カ所から投げた方角の交点に遺跡があるので
中学で習った y=ax+b を使って一次連立方程式を解くだけ




まずF3でデバッグを出してからパールを投げる
パールが飛んだ方向を画面の中心に合わせてSSを撮る
x と z と f をメモる
これを離れた2点でやる

地点1  x1=-35,　z1=576,　f1=70.5
地点2  x2=-1,　z2=850,　f2=115.2

マインクラフトの座標はxが東西で東が正、zが南北で南が正となっている
fは方角で単位は度(degree)
南が0で北が180になっている

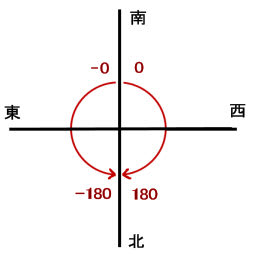
グラフでは便宜上、上方向を南(z)、右方向を西(-x)とする
おなじみの一次関数 y=ax+b は

　z=-ax+b

となる

まず方角から傾きaを求める
直線の傾きは a=tanθ である

しかし角度の基準がz軸から始まっているので
図のように求める角度θは θ=90-f となる

よって地点1、地点2の直線の傾きa1, a2は

a1=tan(90-f1)=tan(90-70.5)=tan19.5=0.35
a2=tan(90-f2)=tan(90-115.2)=tan(-25.2)=-0.47

　　※タンジェントの計算はwindowsの関数電卓でできる
　　　tan(-25.2)　の場合は　25.2　と打ってから　+/-　を押し、左側の　tan　を押す

この値を z=-ax+b に代入して、切片b1, b2を出す

地点1の切片b1は
576=(-0.35)*(-35)+b1
b1=576-12.25=563.75

地点2の切片b2は
850=-(-0.47)*(-1)+b2
b2=850+0.47=850.47

よって方程式は以下のようになる
z=-0.35x+563.75　　…①
z=0.47x+850.47　　　…②

これらを連立すれば遺跡の座標が求まる
①から②を引けば
0=-0.82x-286.72
0.82x=-286.72
x=-349.7

これを①に代入して
z=-0.35*(-349.7)+563.75
 =686.1
 
計算で出した遺跡の座標は四捨五入して
　x=-350,　z=686
の場所にあることがわかる

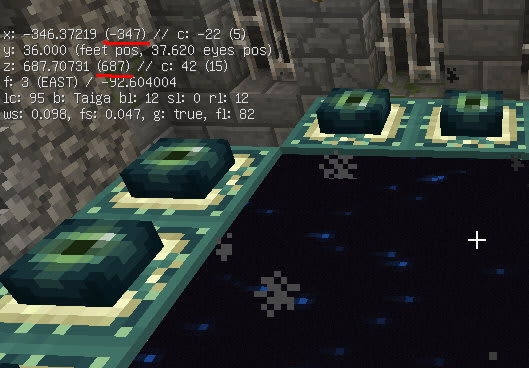
だいたいあってた