離れた2カ所でエンダーパールを投げて、
その座標と方角から遺跡(要塞)の場所を特定しようと思った
計算式が見つからないからここにメモ
理屈は単純
2カ所から投げた方角の交点に遺跡があるので
中学で習った y=ax+b を使って一次連立方程式を解くだけ
まずF3でデバッグを出してからパールを投げる
パールが飛んだ方向を画面の中心に合わせてSSを撮る
x と z と f をメモる
これを離れた2点でやる

地点1 x1=-35, z1=576, f1=70.5
地点2 x2=-1, z2=850, f2=115.2
マインクラフトの座標はxが東西で東が正、zが南北で南が正となっている
fは方角で単位は度(degree)
南が0で北が180になっている
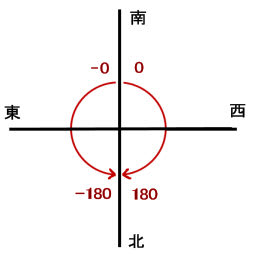
グラフでは便宜上、上方向を南(z)、右方向を西(-x)とする
おなじみの一次関数 y=ax+b は
z=-ax+b
となる

まず方角から傾きaを求める
直線の傾きは a=tanθ である
しかし角度の基準がz軸から始まっているので
図のように求める角度θは θ=90-f となる
よって地点1、地点2の直線の傾きa1, a2は
a1=tan(90-f1)=tan(90-70.5)=tan19.5=0.35
a2=tan(90-f2)=tan(90-115.2)=tan(-25.2)=-0.47
※タンジェントの計算はwindowsの関数電卓でできる
tan(-25.2) の場合は 25.2 と打ってから +/- を押し、左側の tan を押す
この値を z=-ax+b に代入して、切片b1, b2を出す
地点1の切片b1は
576=(-0.35)*(-35)+b1
b1=576-12.25=563.75
地点2の切片b2は
850=-(-0.47)*(-1)+b2
b2=850+0.47=850.47
よって方程式は以下のようになる
z=-0.35x+563.75 …①
z=0.47x+850.47 …②
これらを連立すれば遺跡の座標が求まる
①から②を引けば
0=-0.82x-286.72
0.82x=-286.72
x=-349.7
これを①に代入して
z=-0.35*(-349.7)+563.75
=686.1
計算で出した遺跡の座標は四捨五入して
x=-350, z=686
の場所にあることがわかる
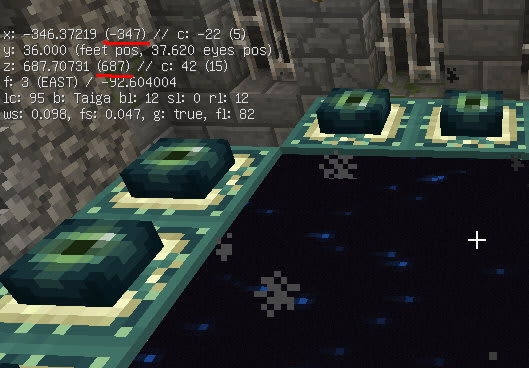
だいたいあってた















