節へのリンク
1.表題書籍について
2.表題書籍の目次
3.表題書籍以外でのIUT理論のインフォーマルな説明について
4.IUT理論の特徴について
4.1 「ガウス積分」の計算との共通点
4.2 「遠アーベル幾何」と「宇宙際」は「鶏」と「卵」の関係かも
4.3 「正則構造の歪み」-- どこから来て、どこにあるのか
4.4 「抽象的な(非線形の)圏」は「腐海」なのかも(笑)
4.5 「IUT語」の特異性について
関連記事
更新履歴
1.表題書籍について^
出版社のページは、「IUT理論4部作」の査読完了を契機に更新されている。
https://www.kadokawa.co.jp/product/321802000140/
「著者 加藤 文元
定価:1,760円(本体1,600円+税)
発売日:2019年04月25日
判型:四六判
商品形態:単行本
ページ数:304
ISBN:9784044004170
人類に残された最後の超難問、ABC予想に挑む!
★2020年2月5日、望月新一教授がIUT理論を展開した論文が専門誌についにアクセプト!
超難問「ABC予想」も証明★
...
本書では、理論のエッセンスを一般の読者に向けてわかりやすく紹介。その斬新さと独創性を
体感できる。理論の提唱者である望月新一教授の特別寄稿も収録!」
関連情報を含め、下記ブログの記事が非常に良くまとまっている。
https://blog.goo.ne.jp/ktonegaw/e/f77f5bd8e1b3c96acd62fba729dc9b4e
「宇宙と宇宙をつなぐ数学 IUT理論の衝撃: 加藤文元
2019年04月29日 17時06分59秒 | 物理学、数学
...
https://youtu.be/kq4jbNl4lJk
未来からきた論文、異世界の論文と呼ばれ、世界で理解している数学者はたった数名という
# 2023-02-15: 望月本人による解説論文の一つ(略称 [EssLgc])* 2022-11-28 版によれば、
# 今では数十名(roughly on the order of 10)の数学者が理解している。
超難解な理論であるにもかかわらず、動画をご覧になっていただくとわかるように、中学生
でも理解できそうな講演だ。
...
中学生にもわかってもらうようにするため、本書では群論の説明に第6章と第7章で50ページを
あてている。
...
講演動画の最後で、加藤先生は「IUT理論は他の数学の問題に対しても使うことができると
思う。」とおっしゃっている。また加藤先生が主催された「数学愛好家の集い」に参加して、
直接お聞きしたのだが「今回の本は中学生以上を対象にして書いたが、理系大学生向けに
もっと深く説明することもできる。」ということだそうだ。....」
↑
理論構造の核心部分に、「遠アーベル幾何:「非可換で十分複雑な群作用を基に「代数幾何/
数論幾何」での「図形」の性質を再現する理論」が出て来るので、群論についてだけは多少
「フォーマル」な説明を「中学生向け」と言えども「せざるを得なかった」わけだが、他は、
一貫して「インフォーマル」な語り口で書かれている。しかし、インフォーマルで平易な見た
目に囚われて「数学的内容がない」とか「具体例がない」とか書き散らす、物分りの悪い人も、
世の中にはいるようだ。インフォーマルで平易な記述にも関らず「意外なほど、数学的内容に
踏みこんでいる」ことが、望月の講演用資料や星裕一郎の解説論文と見比べると分かってくる
ので、後述する。
2023-02-15: 「検証に必要な資質」の観点から、別の歴史的難問の解決と比較して見よう。
3次元ポアンカレ予想は、もともと「代数的位相幾何」の問題として定式化された。ところが、
ペレルマンによる「サーストンの幾何化予想」の一部としての解決は、微分幾何/大域解析学
など他分野の手法を駆使するもので、「伝統的な「位相幾何学」の専門家」たちには、「理解
できそうもない」事が一見して明らかだったため、そうした専門家たちは、かなり「がっかり」
していたようだ。結局、ペレルマンの論文は「彼が駆使した手法の専門家」たちによって検証
されるほかはなかった。
とは言え、少なくとも「伝統的な「位相幾何学」の専門家」たちは、ペレルマンの論文を攻撃
するほど愚かではなく、必要な知識を持つ他分野の専門家たちの検証を見守る見識があった。
ところが、IUT に関しては、「不見識の極みで恥知らず」な連中が湧いて、マスメディアや
ネットで、そうした連中の下らないゴシップが学術的意見であるかのような誤解を広める事に
手を貸す無責任な連中も出てきてしまったわけだ(別記事1*、2*での説明参照)。
また、「ケプラー予想(を解説した書籍)」のp.229 に「シアン」が学術誌に発表した論文の
誤りを指摘する論文を「ヘールズ」が同じ学術誌に発表し、その論文が受理されてシアン論文が
否定された経緯が書かれている。ショルツェらが、主張の証明を含む論文を学術誌に発表した
ことはなく、前掲書に登場する「証明失敗事例」の「文書中で主張の証明にならない言い回しを
多用し、相手との対話を回避する」様子は、ショルツェらの文書や態度と酷似する。
昔、I先生が講義中の雑談で「「分からない」と言っても「(特定箇所が)分からない(1次)」、
「どこが分からないか分からない(2次)」、「「どこが分からないか分からない」という
状態であることが分からない(3次)」のように N次の「分からない」が存在する」という、
その時は全く笑えなかった^^;冗談?を口にされていた事を、ふと思い出した。ショルツェら
RCS-IUT の唱導者の IUT 理論への無理解は、I先生流に言えば、少なくとも3次以上なので、
不明点を質問する事もせず、IUT への奇妙な思い込み(Voodoo Hypothesis * [ EssLgc] *
1.5.1(2022-11-28 版では p.16))に基づく無意味な言説を繰り返すわけだ。
# 注)I先生は2011年に亡くなられた、表現論の専門家。
2.表題書籍の目次^
IUT理論に関連する新たな用語や概念を一度に出すと「消化不良」を起す人が出ることを懸念
してか、「少しずつ小出しにして慣れてもらう」方針というか、小説などの「伏線」に相当する
「(基になった講演での)話の組み立て」なのか、IUT 理論関連の新しい用語や概念は、下記で
ページ番号を書いた所で出てきているようだ 。ページ番号を書いていない所でも、それまでに
出た用語や概念をまとめたり、説明を補足する意味で重要な節がある。
第1章 IUTショック
「イエス、グーグル」
国際、銀河際、宇宙際
未来からやってきた論文
数学界の反応
共通の言語
コミュニケーションパラダイム
たし算とかけ算を分離する p.43-44
「いざない」
最良のコミュニケーション
IUT語
第2章 数学者の仕事
数学で新しいことができるのはなぜか?
数学が進歩するとは、どういうことなのか?
数学とは異種格闘技戦である!
論文の価値はなにで決まるのか?
数学は体力を使う学問である
「興味深い」ということ
理論はいかにして世界へ発信されるのか?
数学はお金がかかる学問である
数学のジャーナル
論文がアクセプトされるとはどういうことなのか?
紳士のゲーム
そもそも人はなぜ数学するのか?
純粋と応用
楕円曲線とICカード p.87-89
ありふれたサクセスストーリー
数学の限りない可能性
第3章 宇宙際幾何学者
数学の変革
32歳で京大教授
焼肉とドラマ
ディオファントス方程式 p.107-109
実効版モーデル予想 p.109-116
タイヒミュラー理論 p.116-121
遠アーベル幾何学 p.121-123
ホッジ・アラケロフ理論 p.123-125
自然であること
アナロジー p.128-133
第4章 たし算とかけ算
素数と素因数分解
根基
ABCトリプル
例外的ABCトリプルとABC予想
強いABC予想
その波及効果 p.150-152
そもそも予想とはなにか?
予想はなぜ可能なのか?
気まぐれな素因数
たし算的側面とかけ算的側面
素数が現れるタイミング
たし算とかけ算の絡み合い
第5章 パズルのピース
IUT理論の新しさ p.171-173
数学の舞台 p.173-177
学校で教わる数学
研究における数学
IUTパズル p.183-186
たし算とかけ算による正則構造 p.186-188
新しい柔軟性
入れ子宇宙
異なる舞台のピースをはめる
テータリンク p.197-201
第6章 対称性通信
複数の舞台で考える p.202-204
舞台間の通信はどうするのか?
対称性
回転と鏡映
対称性による復元 p.212-214
復元ゲーム p.214-217
対称性通信 p.217-221
ひずみ p.221-222
第7章 「行為」の計算
右向け右!
行為の合成
「動き」を計算する
「閉じている」ということ
記号の計算
記号化のご利益
対称性の群
アーベル、非アーベル、遠アーベル p.245-248
文字の置き換えゲーム
対称群
抽象的な群
対称性は壁を越える p.259-262
ガロア理論と「復元」
第8章 伝達・復元・ひずみ
IUT理論がやろうとしていること
目指す不等式 p.268-272
異なる数学の「舞台」のパズルのピース p.273-275
対称性と計算 p.275-278
テータ関数 p.278-280
ひずみの計測 p.281-283
局所と大域 p.283-286
精密な同期 p.286-290
まとめ
おわりにかえて 川上量生(株式会社ドワンゴ顧問)
3.表題書籍以外でのIUT理論のインフォー マルな説明について^
# 2023-03-09: 「柔かさ」では表題書籍以上だが、IUTの技術的詳細にまで言及している
# 望月自身の解説が、本人のブログ記事に掲載されている。e.g.
https://plaza.rakuten.co.jp/shinichi0329/diary/201705060001/
↑ドラマ「逃げ恥」になぞらえた解説
https://plaza.rakuten.co.jp/shinichi0329/diary/201701060000/
↑「サイマジョ」の歌詞になぞらえた解説
https://plaza.rakuten.co.jp/shinichi0329/diary/202205020000/
↑(NHK の放送内容への訂正の意味合いの)球面の幾何になぞらえた解説
従来数学での「局所と大域(の原理)」について、望月新一の論文ページの下記が分かりやすい。
多項式の解の近似がとりもつ数論と幾何の関係 (1), (2), (3), (4).
IUT 理論は、この文献にある「分かりやすい方法」では「局所」から「大域」に移行できない
状況を「何とかする」ために考案されたという説明が表題書籍 p.287 『精密な同期』にある。
「「望月教授の講演のタイトルは、いつも「宇宙際タイヒミュラー理論へのいざない」という
ものでした。」という一節が表題書籍p.45の最後の2行(「いざない」の節の中ほど)にある。
それらの講演資料が、下記にある。
https://www.kurims.kyoto-u.ac.jp/~motizuki/ ↓(Home) から[出張・講演]
https://www.kurims.kyoto-u.ac.jp/~motizuki/travel-japanese.html
資料番号 [12], [13], [15], [16]. [17]
(各々の講演時間等の都合で)内容に多少増減があるが、「「qNとqを、「同じものであるかの
ように」対応付ける」方法があれば、いろいろな「ディオファントス方程式(を数論幾何の対象
として考えたもの)」についての不等式を導出できそうに思える」というアイデアが、いずれも
最初の方で提示される。つまり、前節の目次で『テータリンク』、『目指す不等式』... にある
説明と同じことを、理論の提唱者自身も述べている。上の資料では、指数が Nの代りに j² と
なっているが、星裕一郎による下記の資料などでは N が使われており、本質的な違いではない。
https://www.kurims.kyoto-u.ac.jp/~yuichiro/talk20151201.pdf
なお、理論の応用は「ディオファントス方程式の幾何」で、具体例がABC予想(∴シュピロ予想、
実効版モーデル予想...)である。「初等的な例」がないなどと「無い物ねだり」で表題書籍に
文句をつけている変な人もいるようだが、*そんなものは、存在しそうにない*ことくらい、
この理論がどんなものかの説明から、分からないのだろうか。
「たし算とかけ算の関係を保ったまま」では、言い換えると「体や環の同型」という従来の数学
での関係からは「qN と q は全くの別物」だし、「ガロア群」も「和を保つ写像の群」なので、
従来の枠組みの範囲内。しかし、いったん和を忘れて「かけ算と群の数論幾何的図形への作用」を
考えれば、*局所的には*「qN と q は同じようなもの」としての扱いが可能になる。さらに、
(従来数学での「局所から大域への移行」の仕組みと比較すると途方もなく大仕掛けにはなるが)
遠アーベル幾何の応用により「数体を復元」する計算手順を構成できる ... ただし、計算手順の
各段階で生ずる「ひずみ」あるいは「不定性」があるので、計算結果は不等式の形になるという
言い方は、表題書籍と星裕一郎の下記概説論文「宇宙際Teichmüller理論入門」で共通である。
https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/244783
Kyoto University Research Information Repository: 宇宙際Teichmüller理論入門
(On the examination and further development of inter-universal Teichmüller theory)
「これまで考察/構成を行ってきた様々な概念を用いることで, (Ind1), (Ind2),(Ind3) という
不定性 のもと, (ある適切な設定において)
(a) 対数殻
(b) 楕円曲線の q パラメータの (1 より大きい) ある有理数による巾
(c) 数体
を多輻的に表示することができる.」(←「宇宙際Teichmüller理論入門」本文最後の文章)。
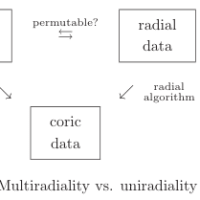
ただし、「宇宙際Teichmüller理論入門」では「多輻的な表示」、「多輻的アルゴリズム」と
「多幅的 (multiradial) 」というキーワード(定義には手間がかかる)が出てくるが、これは
表題書籍で『精密な同期』という節の表題としてのみ言及されている「多数の宇宙での整合的な
計算」に必要な条件。
# multiradial という概念について、「望月新一の過去と現在の研究」にイメージ動画がある。
# また、 資料「過去と現在の研究の報告」(2008-03-25)は、「IUT の着想に至るまでの経緯」を
# 知る上で、極めて有用。
# 別記事でも言及した山下剛による「“宇宙際” についての FAQ 」p.2 A4 に multiradial という
# ↓概念の説明がある。
# 「同一視はできても本来的起源が違う対象を別のものと思う sensitive な感覚が宇宙際
# Teichmüller理論では大事になってきます. R² に異なる 2 つの正則構造を入れると,
# どちらも C で同じものです. 正則構造のみしか見えない視点では両者をつなげることは
# できませんが, 下部構造の R² を考えると非正則なつながり方が見えてそのズレを計る
# ことができる, ということと類似のことを宇宙際 Teichmüller 理論ではします.
# つまり, 数体の数論的正則構造 (=環構造) を非スキーム論的に変形し, 変形前と変形後は
# 環としては同じものですが, スキーム論だけでは見えないそのつながり方を
# mono-analytic な 視点を導入して見えるようにしてズレを計算する, ということをします.
# 宇宙際 Teichmüller 理論ではそのようにある1つの数論的正則構造の視点でのみ意味を
# もつ性質を uniradial と呼び, 他の数論的正則構造たちとも共通する性質を coric と呼び,
# ある数論的正則構造の視点で別の数論的正則構造たちを記述できる性質を multiradial と
# 呼んでいます.」
# 2023-03-14: これらの概念の定義は圏論による。e.g. 山下剛のサーベイ論文p.252-p.253
表題書籍での「対称性通信」が論文では「単遠アーベル的輸送」という用語になっているほか、
「対数殻」は局所的概念(つまり「p進対数」の値域)と明示されていたり、「入門」とは言え、
さすがに論文の方は、用語だけ見ても「骨がある」というか「骨が折れそう^^;」な印象を受ける。
# 次節に同論文を始めとする「やや数学用語の使用が多い概説文書」と表題書籍を見比べて
# 解った事を、いくつか書き出しておく。
数学的に「より厳密」にした続編もある(さらに厳密な文献=望月の「4部作」論文。また、
山下のサーベイ論文は同程度に厳密)。しかし、「IUT理論について、専門家でない人にも、
できるだけ、その基本思想が分かるように」という目標を掲げた書籍として、十分に理論の
「数学的内容」が記述されていることは、いまや明らかであろう。
# 2022-11-04: 前記「 望月の研究」ページとの重複もあるが概説文書について補足。
# 下記文書↓の 1.-6 は「素人の説明にしては」ではあるが、「よく書けている」印象。
# https://www.jstage.jst.go.jp/article/essfr/6/3/6_160/_pdf
# (少なくとも、↑本ブログ筆者より巧みに説明しているような気が ... ^^; )
# より数学的な概説としては、まず星裕一郎の前記論文や講演スライド集があり、
# https://www.kurims.kyoto-u.ac.jp/~yuichiro/talks.html
# 山下剛の論文や講演スライド集もある。
# https://www.kurims.kyoto-u.ac.jp/~gokun/myworks.html#IUT
# なお、この種の概説としては、Ivan Fesenko の解説記事とサーベイ論文が、長さと用語の
# 難易度の観点から(英語だが^^;)最も「取っつき易い/技術的詳細を極力省いた」説明。
元々の(リーマン面の擬等角写像変形の)タイヒミュラー理論とのアナロジーから「正則構造」
という用語が命名され、「等角写像」↔「環や体の同型」、「擬等角写像」↔「リンク」
という対応を意識して、理論名を「宇宙際*タイヒミュラー理論*」にしたと考えてよさそうだ。
(「リンク」は「集合間の写像」ではなく圏論的な対応で、概念の抽象度は違うが。^^;)
下記文書↓は「IUT 理論を勉強する際の心得」の「経験者による貴重なコメント」を含んでいる。
Tan --- Introduction to inter-universal Teichmüller theory (slides).pdf
先頭スライド (Reading IUT) を引用しておく。
To my limited experiences, the following seem to be an option for people who wish
to get to know IUT without spending too much time on all the details.
* Regard the anabelian results and the general theory of Frobenioids as blackbox.
* Proceed to read Sections 1, 2 of [EtTh], which is the basis of IUT.
* Read [IUT-I] and [IUT-II] (briefly), so as to know the basic definitions.
* Read [IUT-III] carefully. To make sense of the various definitions/constructions
in the second half of [IUT-III], one needs all the previous definitions/results.
* The results in [IUT-IV] were in fact discovered first. Section 1 of [IUT-IV] allows
one to see the construction in [IUT-III] in a rather concrete way, hence can be
read together with [IUT-III], or even before.
S. Mochizuki, The étale theta function and its Frobenioid-theoretic manifestations.
S. Mochizuki, Inter-universal Teichmüller Theory I, II, III, IV
# 2023-03-09: 山下剛が「望月の四部作論文」検証の一環として執筆したサーベイ論文
# 「A Proof of The ABC Conjecture after Mochizuki」は表題の示す通り、ABC 予想の証明
# への興味から IUT 理論を知ろうとする場合への配慮が行き届いた構成になっている。
# 「四部作論文」の次くらいに「フォーマル」度が高い解説ではあるが、導入部や付録には
# 多少「くだけた」説明もある。
4.IUT理論の特徴について^
前述のように専門家による多くの解説資料があるので、「(より)正確な説明」は、それらを
見て頂くことを前提に、ここでは「筆者の(素朴な^^;)理解」を述べる。
(1) 「ガウス積分」の計算との共通点
(2) 「遠アーベル幾何」と「宇宙際」は「鶏」と「卵」の関係かも
(3) 「正則構造の歪み」-- どこから来て、どこにあるのか
(4) 「抽象的な(非線形の)圏」は「腐海」なのかも(笑)
(5) 「IUT語」の特異性について
4.1 「ガウス積分」の計算との共通点^
IUT 理論と「ガウス積分」の計算との類比は、望月による説明では頻繁に登場する。
「21世紀の新しい数学」にあった「ガウス積分とIUT理論の類似」について、上記解説資料や
サーベイ論文に「足し算とかけ算の対」から「かけ算と群の数論幾何的図形への作用の対」に
移る操作が「座標変換」に対応し、理論に登場する多くの「宇宙」が「座標平面」に対応する
という趣旨の説明がある。
# 2023-05-22: 山下剛の「“宇宙際” についての FAQ」 p.2 A4 でも宇宙替えと座標変換の類比を
# 後者を「おもちゃ版」として言及。Ivan Fesenko の解説記事やサーベイ論文にも言及がある。
- The Mathematics of Mutually Alien Copies
- A Panoramic Overview of Inter-universal Teichmüller Theory
多分、「(考察対象の)異なるラベルを持つ複数のコピーによって、考察の舞台を作る事」が、
最も基本的な共通点であろう。
ガウス積分の場合、積分変数名が異なる2つのコピーにより、「平面」という舞台での積分を
考察することで、1変数での積分での操作(置換積分や部分積分)では考えようのなかった操作
である二変数での座標変換が可能になる。
極座標への変換で、「元の積分と似ているが置換積分が有効になった部分」と「新たに発生する
「平面(=複数のコピーによる舞台)固有の部分」に分けた計算が可能になって、問題が解決。
ガウス積分を極座標で「円周」と「半直線」に分けて積分する事と、IUT理論で数体の整数環に
含まれる乗法モノイドへの群作用を「1の巾根」部分への作用と「(絶対)値」への作用に分けて考察
する事との並行性、「極座標への変換が有効な理由」が「被積分関数がフーリエ変換で形を変えない」
ことと関係し、さらに「回転群としての S¹ の平面への作用」との関連を見たときに「群作用の剛性」
の本質的役割という類似性がある ... といった話もあるようだ。
IUT 理論では、下記のような対象を「宇宙ごとにある、一組のデータ」として、データへの操作を
「遠アーベル幾何」を利用した「群作用からの構造の復元」で宇宙間で対応を取りつつ考察する。
{数体、数体のガロア群(の数体への作用)、数体上の楕円曲線の等分点、数体の整数環が含む
乗法モノイド、数体の各素点毎の対数、....}
こうすることで、環論(スキーム論)的考察では考えようのなかった「多輻的表示」を利用しての
計算が可能になって、問題が解決。この「多輻的表示」の実現の際、群作用の剛性が決定的に重要。
4.2 「遠アーベル幾何」と「宇宙際」は「鶏」と「卵」の関係かも^
宇宙間での前述のデータの対応として、「環や体の準同型に成り得ないもの」を考察するため、
データの対応付けで「環としての構造に依存する属性を忘れても意味を持つ特徴」に着目する。
例えば、「ガロア群」そのものではなく「ガロア群と同型な位相群」として対応させる。すると、
位相群としての同型写像は「沢山ある」ので、考慮すべき同型対応の可能性の全てを尽すため、
無数のコピーからなる舞台が必要になる。
各素点毎の対数も各宇宙での環としての構造に依存するほか、無数の素点での状況を考慮する
必要性からも、やはり無数のコピーからなる舞台が必要になる。
「無数のコピーからなる舞台」として、考察する宇宙間の対応の種類に応じた「ホッジ劇場」を
構築する。四部作論文の最初の一つは、丸ごと「ホッジ劇場の構築」がテーマになっている。
「別の宇宙のデータとの対応」という設定は、「環構造のある対象間の環準同型でない対応」を
考える際、概念の混同による誤った推論を避ける上で極めて有効(そのための「宇宙際」)。
宇宙間で整合性のある(そのため、個々の宇宙内でのデータの操作や計算としても意味を持つ)
「環としての計算」の仕組みを、遠アーベル幾何での「数体の復元」を基礎に構築し、問題を
解決するのが IUT 理論の基本方針。
逆に言えば、「遠アーベル幾何で群作用からの「数体の復元」が可能」という認識を予め持って
いたからこそ、「「抽象的な位相群としてガロア群」のような環構造に直接依存しない「データ」
から、同型な環の異なるコピーの間に、環同型とは異なる対応を定める具体的手順を構成する」
という発想が可能だったとも言えよう。
従って、遠アーベル幾何は IUT 理論の必要不可欠な要素であり、遠アーベル幾何を利用できて
いない RCS-IUT の言説は、それだけで既に IUT と論理的に同等ではあり得ないことが明らか。
イヴァン・フェセンコのショルツェとスティックスのレポートへの評価での指摘参照。
表題書籍の対応箇所:
対称性による復元 p.212-214 、復元ゲーム p.214-217 、対称性通信 p.217-221
4.3 「正則構造の歪み」-- どこから来て、どこにあるのか^
2つのタイヒミュラー理論(「古典/元祖^^;」と「宇宙際」)の違いを「正則構造の歪み」の
「起源」と「所在」という視点から整理して見よう。
「元祖」の方では、「(複素数の解析における)正則構造」の歪みが、「各実2次元の曲面に、
最初から「それぞれ異なる複素構造」が定義されている」状況、つまり「「集合」に「構造」を
導入する」という「集合論的な枠組み/発想」の範囲で、*存在自体は*当然視される。
# ↑しかし、「集合論を認めない(クロネッカー的)立場」からは、異議があるかも??^^;
「宇宙際」の方では、「(環構造の別名としての)正則構造」の歪みが、「乗法とだけ両立する
リンク」が「異なるラベル付けがされた他の「コピー」との間に設定された状況」から、言わば
「あぶり出される」。つまり、「歪み」は「(ラベルで区別されるだけの)最初に環構造が定義
された集合」自体の上にではなく、様々なリンクが設定された「舞台」の上で可視化されている
という意味で、「圏論的な枠組み/発想」により、存在が示される。そして、具体的計算手順も、
この舞台の上で構築される。
環構造が定義されている集合上に最初の環構造とは違う構造が直接導入されるわけではないので、
「集合+構造=数学的対象」という図式への「(無意識の場合を含む)拘泥」が、歪みの存在を
認めることを(無意識の場合を含み)拒否させてしまった結果が、RCS-IUT 症候群だと思われる。
# 望月の「2018年3月討議レポート」[Rpt2018] に、この症状の記述がある。
しかし、*歪みの起源は、各宇宙のデータの組を起点とするリンク*なのだから「歪みの担い手」
として各宇宙のデータを見ることも、「圏論的な枠組み/発想」に立てば自然に思えるのだが。
こう言うと、「現代数学では圏論の利用は常識で、圏論的発想が欠けた数学者などいないはず」
との反論をされる向きもあろうが、過去の IUT ワークショップでは「なぜ数論で圏論が必要か
分からない」といった質問が飛び出した例すらあると言うし、一口に圏と言っても、種類により
様相が大きく異なり、慣れ親しんでいない圏では「勝手が違う」こともありうる ...
「宇宙際Teichmüller理論入門」p.98 l.17-l.26
「そもそも数論幾何学の研究において, “様々な環の環構造の放棄” という行為自体が既に
非常に珍しいと思います. 例えば Galois 表現をその主要な対象とする数論幾何学の研究の
場合, 表現空間の基礎環 ? つまり, 典型的には “GLn(?)” の “(?)” のところに登場する環 ? の
環構造を放棄するわけにはいきません. また、遠アーベル幾何学と同じく “圏の構造による
代数多様体の復元” ... 例えば, ... 代数多様体の(準) 連接層のなす圏やその導来圏から元々の
代数多様体を復元する研究の場合 .. .考察下の圏は“基礎体上の線型的な圏” ,して取り扱わ
,れるため, ... 基礎体の環構造を放棄するわけにはいきません. ....」
4.4 「抽象的な(非線形の)圏」は「腐海」なのかも(笑)^
前節 4.3 に関連して、ふと、K² 先生が、講義中の雑談で「「群の圏」はアーベル圏でない。
だから、群論は難しいのだと思う。」といった趣旨の話をされていたことを思い出した。(その
講義自体の内容は、さっぱり思い出せないが ^^;)なお、K² 先生は、著名な数論の専門家。
思うに、一部の(自分の専門分野では、それなりに有能な)数学者が IUT 理論を理解し損ねる
一因は、「非線形の圏」にアーベル圏的なイメージを無理に(無意識に)当てはめようとして
しまっているためかも知れない。IUT 理論での圏は、「基礎体上の線型的な圏」ですらないので、
アーベル圏的なイメージは全く適用できない“抽象的な圏”であり、「対象を射の起点と終点を
示すラベルとして捉える」圏論本来の思想に沿う扱いが、決定的に重要なのだと思われる。
アーベル圏は「Mitchel の埋め込み定理」によって、ある環 R の R-加群のなす圏だと思える
から、圏の対象は「集合に、その集合上で定義された構造が入ったもの」というイメージとの
齟齬が生じない。しかし、IUT理論で扱う圏は、そうではない。 Wikipedia での 群の圏の項で、
「そもそも射の集合に加法が定義できない」ので加法圏ですらないとの説明がある(加法圏の
定義に即して言えば、「圏論的直和が群の自由積であり、圏論的直積である群の直積と異なる」
から「加法圏」ですらなく、従ってアーベル圏ではない。)
アーベル圏系統の線形圏の理論しか使っていない数学者には IUT の抽象的な(非線形の)圏が
名作アニメ「風の谷のナウシカ」の「腐海」のように危険なのだという仮説を提起する。:-)
ナウシカを含む「風の谷の住人」は、「腐海」での適切な振舞いが身についていて比較的安全に
行動できるが、「よそ者」は「腐海」において致命的な行動を、簡単にとってしまう。
# IUT や遠アーベル幾何の専門家は「風の谷の住人」で、RCS-IUT 唱導者は典型的「よそ者」^^;
なお、「腐海」が実は「汚染された世界を浄化する場所」であり、イメージが冒頭と終幕では
全く違う事にも注意しておこう。
4.5 「IUT語」の特異性について^
「構造を持つ対象の圏で、その射が構造を保たないものを考えても、めったに役に立たない
(「ベーシック圏論」p.42 例 1.3.23)」という一般論が、IUT 理論には当てはまらない。
ただし、2つある環の演算「たし算」と「かけ算」のうち、「かけ算」だけは常に保つ i.e.
乗法モノイドとしての構造は保つ射を考えるので、「ベーシック圏論」例 1.3.23 とは違う状況
(+「遠アーベル幾何」により「たし算」の対応も復元する i.e.「たし算とかけ算を分離する」
のであって、「たし算を完全に無視する」のではない)を考えてはいる。しかし、「一宇宙内に
閉じて、環構造を前提にした (= uniradial) 」計算」以外に、「複数宇宙の「精密な同期」を
前提にした (= multiradial) 計算」が可能になる理由は、「たし算」を(完全には)保たない
対応を射として考えるからに他ならない。よって、「抽象的な圏」による考察の中でも、かなり
特異なパターンが駆使されていることになりそうだ。
さらに、ガロア群を「体への作用」をいったん忘れて「抽象的な位相群として扱う」こと、及び
「位相群としての同型全て」をまとめて "poly-isomorphism" として扱うあたり、ある意味
従来の「圏論」の枠組みをはみ出す考え方も含んでいる。四部作論文の最後に置かれた
"Log-Volume Computations and Set-Theoretic Foundations" の最後のセクションの表題
"§3. Inter-universal Formalism: the Language of Species" の最後の単語 species が、
「従来の「圏論」の枠組みからはみ出す考え方」での鍵概念ということで、同論文の p.67 から、
「フォーマル」な形で説明されている。この概念の「効用」は同論文 p.75 l.9-l.13 にある。
"the notion of a “species” allows ... roughly speaking, to “simulate
∈-loops” -- without violating the axiom of foundation".
アイデアとしてはIUT 研究の早期に得られていた: 2004年時点の講演資料p.1 §1.2 参照。
因みに、ショルツェらは、この species 概念{を、も}理解し損ねている。本概念の構成に
不可欠な「ラベル付け」を認めないのだから、理解できるはずがない。(山下剛の解説)
なお、Wikipedia にあるショルツェらの「 ... 不等式は無意味になる」という言い草は、
species や multiradial の概念を理解していないことの自白に等しい。
# 別記事1、2で述べたように、ショルツとスティクスが発表した多少とも数学的内容を含む
# 文書で最も詳細なものは[SS2018-8] であり、上記の言い草は、その結論部分に多少文学的
# 修飾を加えているだけ。そして、[SS2018-8] は、その前身[SS2018-5] と共に、望月の報告
# [Rpt2018] および「反批判」の [Cmt2018-5] と [Cmt2018-8] によって粉砕されている。
RCS-IUT の間違いに基づくデマに過ぎないので、言及の必要性自体が疑問。前掲の望月や
山下の指摘で間違いであることは明らか(「ショルツェからの再反論が存在しない」事は、
以前の Wikipedia では言及されていた)。
それにしても、もうそろそろ、Wikipedia での宇宙際タイヒミュラー理論の記述を「数学理論の
説明」らしくすべきではないだろうか。つまり、主要(ないし基本)概念や主要な命題こそが
主な記述内容であるべきで、ショルツェのデマについての記述など、どうでもよいことのはず。
「数学理論の説明」は、例えば、モース理論や岩澤理論の説明のようであるべきだ。