3次元FEMソフトできた！

2次元FEMソフトが完成してから苦節1週間。
ついに3次元への拡張ができました。

（↓2次元FEMの画像）


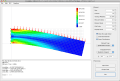
ある程度高い精度を出せるように、
2次元ではアイソパラメトリック四辺形一次要素、
3次元ではアイソパラメトリック六面体一次要素を採用。
積分は8点の2次積分を（2次元では4点）。

[B]マトリクスが煩雑すぎてデバッグで吐きそうになったりしましたが、
懲りずに書いてなんとか動いたときは感動しました。

現状は単純な図形に対してのみの有限要素解析ですが、それっぽい結果の生成が嬉しかったので記念記録。

また、六面体要素1つの要素剛性マトリクスが24×24の行列で、
全体剛性マトリクスは要素の頂点数×3とかなり膨大な行列になってしまうので、
すぐヒープ領域が足りなくなってしまう現状。
起動時にメモリ確保の命令入れても要素数2000くらいでが限界でした。

これからまた、連立一次方程式のメモリに優しい解法アルゴリズムを書く作業がはじまります。
それができたらメッシュ分割アルゴリズムを勉強して、UI整えてそれっぽいもの作りたいです。

大学の研究進めずに何やってるんだろう。

NetBeansでApache Commons Mathを使いたい

これまでひたすらシコシコと全部1からソースコードを書いてきたけど、
最近作業が全然追いつかなくなってしまったため、今更ながら数値計算ライブラリに手をつけることに。
数値計算ライブラリ「Apache Commons Math」をNetBeansで使うまでのメモ書き。

①公式サイトから最新版のBinaries（2011年12月5日時点でver2.2）をダウンロードし、適当な場所に解凍。
http://commons.apache.org/math/

②NetBeansを起動して、[ツール]→[ライブラリ]と進みライブラリマネージャーを起動。

③[新規ライブラリ]ボタンを押して、「ApacheCommonsMath」を追加。

④[JAR/フォルダを追加]ボタンを押して、先程解凍したフォルダから
「commons-math-2.2.jar」と[commons-math-2.2-sources.jar]の2つのファイルを追加。

⑤プロジェクトウィンドウで、目的のプロジェクトの[ライブラリ]を右クリックし、[ライブラリを追加]をクリック。
「ApacheCommonsMath」ライブラリを追加する。

これでライブラリのクラスとJavadocが表示されるようになりました。

NetBeans 7.0⇒7.0.1の地味に嬉しい変更点

今日つかってて気づいた、すごく地味な変更点。

今まで、何か文字を打ってセミコロンを付けずに改行すると、
自動的にインデントされていました。
@から始まるアノテーションでもまた然り。

それが、アノテーションの後はインデントされなくなっていました。
後からアノテーションを追加するときは今までの仕様で全く問題無かったのですが、
自分は結構先に書くことが多いので、地味だけど結構嬉しいです。

例えばJComponentのpaintComponentが次のように記述しますが、

@Override
public void paintComponent(Graphics g){

これを@Overrideアノテーション⇒メソッドの順で書こうとすると
public..の書き始めが字下げされちゃって、バックスペースで消すのが面倒でした。

アノテーションの後にインデントは、
まず間違いなく不要だということでこのような仕様変更になったことと思います。

NetBeans 7.0.1でLook and FeelがNimbusに？

JDK7とNetBeans 7.0.1をインストールして、
JFrameフォームを作ってみたら、look and feelがNimbusになっていて

「うわあああああああああああ」

ってなったけど、ソースコードを見てみたら
mainメソッドの中にUIManagerクラスのsetLookAndFeelメソッドが自動生成されていただけで、

「おぉぅ・・・」

ってなりました。

ちょっと謎仕様でしたが、
バージョンやプラットフォームの違いを考慮した
安全性の高い（と思う）LnF設定のコードは参考になりました。
forループでNimbus LnFがあるかどうか調べて、
見つかったときのみsetLookAndFeelメソッドを呼び出しています。

↓自分がよく使う手抜きLnF設定
try {
javax.swing.UIManager.setLookAndFeel("com.sun.java.swing.plaf.nimbus.NimbusLookAndFeel");
} catch (Exception ex) {
ex.printStackTrace();
}

↓NetBeans 7.0.1で自動生成されていたコード
try {
for (javax.swing.UIManager.LookAndFeelInfo info : javax.swing.UIManager.getInstalledLookAndFeels()) {
if ("Nimbus".equals(info.getName())) {
javax.swing.UIManager.setLookAndFeel(info.getClassName());
break;
}
}
} catch (ClassNotFoundException ex) {
java.util.logging.Logger.getLogger(MPS.class.getName()).log(java.util.logging.Level.SEVERE, null, ex);
} catch (InstantiationException ex) {
java.util.logging.Logger.getLogger(MPS.class.getName()).log(java.util.logging.Level.SEVERE, null, ex);
} catch (IllegalAccessException ex) {
java.util.logging.Logger.getLogger(MPS.class.getName()).log(java.util.logging.Level.SEVERE, null, ex);
} catch (javax.swing.UnsupportedLookAndFeelException ex) {
java.util.logging.Logger.getLogger(MPS.class.getName()).log(java.util.logging.Level.SEVERE, null, ex);
}

愛車が盗まれちゃった

3日間旅行に出かけている間に、
ロードバイク盗まれちゃいました。

悲しい。