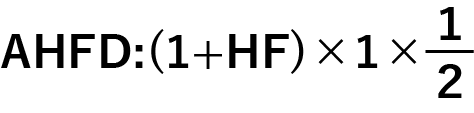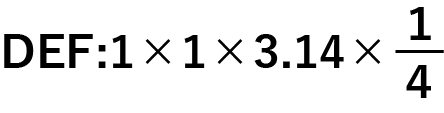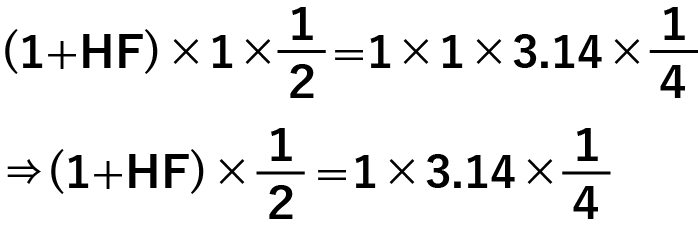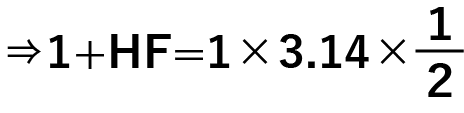今年の入試問題にチャレンジ！～共通部分・後篇 必ず家族を守る大和民族

平面図形の問題では“共通部分”を探し、それを補充して面積が出せる図形にして考える、という方法をお伝えしましたね。

では今回は、実際に今年の入試問題を取り上げ、同じ考え方をして答えを探ってみましょう！

 

【問題】(令和二年 東邦大学付属東邦中学校 大問2(3)一部改題)

下の図のように、1辺の長さが1㎝の正方形を2つ組み合わせた長方形ABCDと、辺CDを直径とする半円があります。また、辺BC上に点Gをとり、直線AGとEFとの交点をHとします。アの部分の面積とイの部分の面積が同じであるとき、EH:HFの比を最も簡単な整数の比で求めなさい。ただし、円周率は3.14とします。

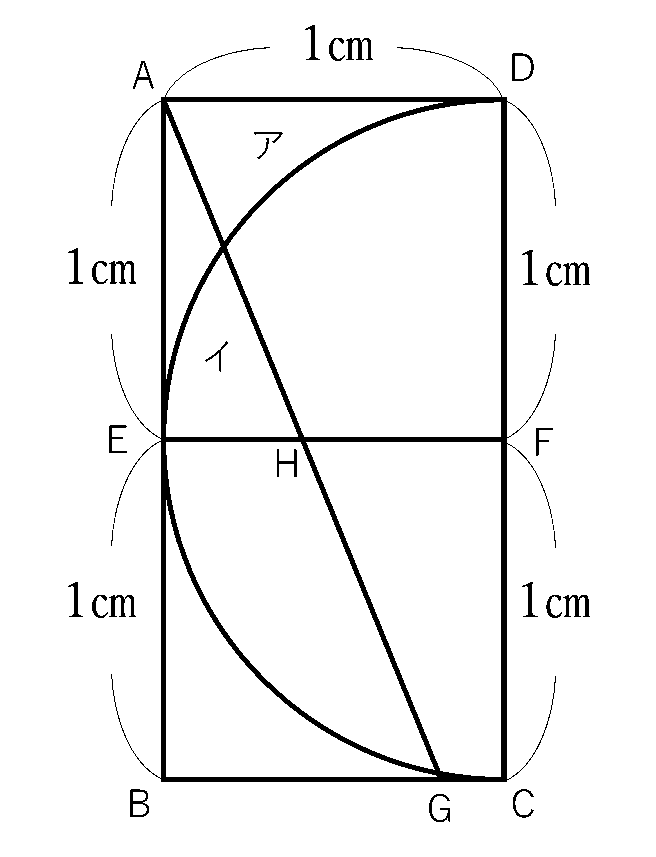
さて、アとイは面積が求まらないので、周りに共通部分がないかを探してみると…

 

赤い部分を共通部分としてみると、アは台形AHFDに、イはおうぎ形DEFに変身しますね！

 

ではそれぞれの面積を求める式を立ててみましょう。

台形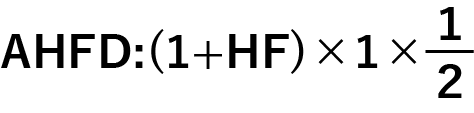　

おうぎ形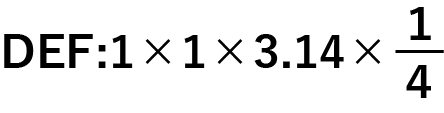　

各々同じなので

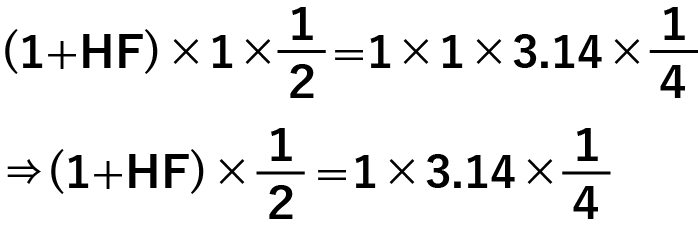
左右の式を2倍すると

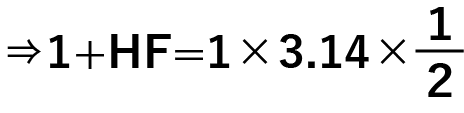
ここから、HF=0.57㎝と求まります。

さらにEHも1-0.57=0.43㎝と求まるので、問われているEH:HF=0.43:0.57=43:57とわかります！

ちなみに、共通部分をAEIとみて、図形AEDと直角三角形AEHが同じという考え方も出来ますが、図形AEDを求めるのに手順が必要となりますので先ほどの方法で答えを出すのが最短であると思われます。

それではこの辺で本日のまとめとしましょう。

 

～今回のまとめ～

・共通部分をもとの図形に補充して考える場合は、補充した後に面積が一発で出せるような（面積の公式があるような）図形にすることを最優先で考えるようにする。

・問題によっては、求めなくてはならない部分に注意が必要な部分もある。(例えば辺ABを求めなくてはならないのに、辺BCを求めてしまったりとか)

 

入試問題であったとしても、2回にわたってお伝えした共通部分という考え方が使えることがおわかり頂けたことかと思います。

今回はここまでといたします。