キセル算 中学算数 中学受験算数 和暦大切

5年生以上のみなさんなら｢キセル算｣について学習したことがあるかもしれません。

 
｢キセル算｣という名前には聞き覚えがなくても、下のような問題だよと言われれば「あ、見たことがある！」という人も多いのではないでしょうか。

 

 

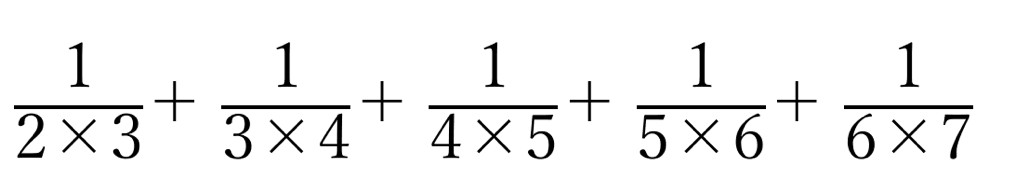
「ああ、これは、知ってるよ！とりあえず…」

 

 

「こんな風に途中の数字を全部消してしまう！あとは、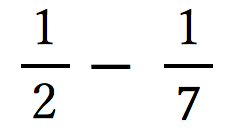分母の最初と最後の数字を見ると2と7が残っているので、と引き算にして計算すればいいんだよねー」

 

なんて、計算のやり方だけを覚えている人が結構いるようです。

 

たしかに結論はこれで合っているですが、そもそもなぜ引き算にするのでしょうか？なぜ、途中の数字を消してしまってよいのでしょうか？

 

このあたりの計算のしくみがきちんと分からないままでは、少しひねられただけで間違えてしまいます。
 

「私はしっかり分かってる！」という人は大丈夫。でも、｢やり方は覚えているけど、これで正しく計算できる理由までは…｣という人は、この機会にきちんと理解しておきましょう。

 

途中を消して筆算にできる理由とは？

 

そもそも、この式に現れるなどの部分は、
 

 

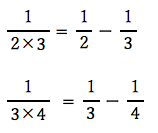
のように、変形できます。確かに、計算してみると上の2つの式の値は、とで、確かに両辺が等しいですね。
そこで、もとの式全体は、

 

 
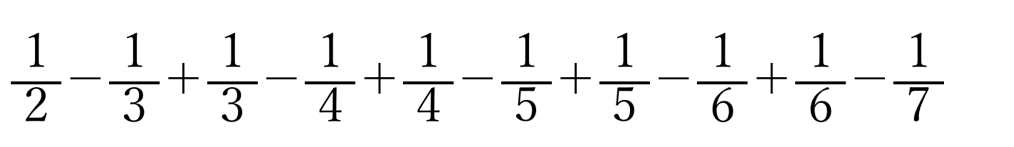
と変形できることになります。確認してみてくださいね。

 

さて、こうなるとから
までの分数は、－と＋をともなって2回ずつ現れていますから…
 

 
こんどはこのように堂々と(？)消すことができ、たしかに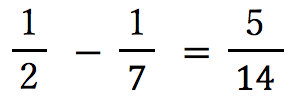と計算できることが分かりました。

 
以上で見てきたように、「キセル算」の計算をするならば、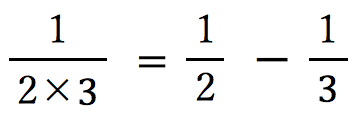のように分数の差に変形できることは少なくとも理解しておかなければなりません。

 

ところで、両辺を計算してみれば確かに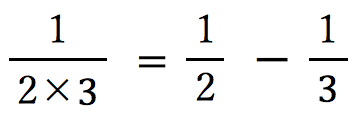になっていることは分かりますが、なぜこのように変形できてしまうのか、ちょっと不思議に思う人もいるでしょう。そんな人には算数のセンスがあるかもしれません。

 

実は、図形的に考えてみるとこの変形の意味や仕組みがとらえやすくなります。

 

そして、やり方だけを覚えている多くの人が間違えてしまう、
 

 

のように少し形を変えられた問題も、本当に仕組みが分かっていれば大丈夫。