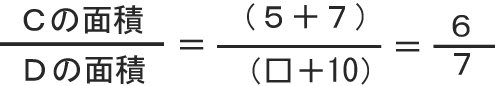作図って むつかしい？

コンパスと定規を使って図形を書く 作図！

これ、苦手だ～と言う人！

あなたあなた！

作図を毎回１から考えていませんか？

作図は、何種類かのパターンの組み合わせです。

どのパターンを使うのか？

そのためには、パターンを覚えて

つぎにそのパターンの使い方を覚えましょう～

 

作図の問題は、結果から考えると

どのパターンが使えるのか？分かりやすくなります。

 

２等辺三角形を書くパターンで

垂直２等分線、直角、角の２等分線、などが書けます。

正三角形を書くパターンで

６０°の角度、正６角形、などが書けます。

 

ほとんどの作図は、この２つのパターンで書けてしまいます。

 

それでは、この２つのパターンを駆使して

次の問題を考えてみてください。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

半径５ｃｍの円と、その中にぴったり入る

同じ大きさの３つの円を 作図してください。

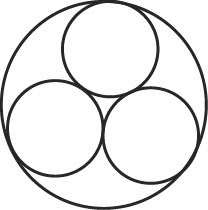
ヒント：結果から考えよう！

できた人は、４つの円が入る場合も考えてみましょう～

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

前回の答え：

列車は、１分１０秒で何ｍ進むのでしょうか？

列車は時速７２ｋｍで走りますから、

１分間に １．２ｋｍ （７２÷６０） これは１２００ｍ

１秒間に ２０ｍ （１２００÷６０）

１分１０秒で １４００ｍ （２０×７０）

その進んだ距離が、トンネルの長さ＋列車の長さ になります。

１４００＝１２００（トンネル）＋列車の長さ

列車の長さは、２００ｍです。

 

今回は、きれいに割り算ができましたが問題によっては

割り切れない場合があります。

そんなときは分数で答えましょう。

苦手な文章問題 列車とトンネル！

苦手な文章問題シリーズ（そんなシリーズいつからできたの？）

その２回目です。

小学校の算数に出てきた問題！

何回聞いてもよく分からなかった～

そんな問題です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

時速７２ｋｍで走る列車が、長さ１，２ｋｍのトンネルを通ります。

列車の先頭がトンネルに入ってから、トンネルを抜けるまでに

１分１０秒かかりました。

この列車の長さは何ｍでしょう？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんなややこしい問題を解かなきゃいけない小学生！

いまだに解けない中学生！

教えようにもよく分からない保護者！

こんな問題を出すから不幸になるんでしょうかね～

いっそのこと賞金付きの問題にすれば目の色が変わるんでしょうが・・・

ただ、この問題は昔からある定番問題で、解き方考え方も定型があります。

それが分かれば九九の中のひとつみたいなもんです。

考え方：

列車は、１分１０秒で何ｍ進むのでしょうか？

その進んだ距離が、トンネルの長さ＋列車の長さ になります。

絵をかいて考えてみてくださいね。

 

答えは次回に！

苦手な文章問題 食塩水～

誰しも、文章問題は苦手です。

今の算数数学では、応用問題として文章問題を作っていますので

計算問題よりは難しくしてあります。

それと、

あまり大きな声では言えないのですが

普通の生活感覚では、ありえないシチュエーションが多く

こんな問題をといても、将来何の役にたつのか？と疑いたくなる問題が

とても多いことも、苦手な人が多くなる原因では？と思います。

 

そんな生活感のない問題！（笑）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

５％の食塩水と１０％の食塩水を混ぜて、８％の食塩水を５００ｇ作るには

５％の食塩水と１０％の食塩水をそれぞれ何ｇずつ混ぜればよいでしょう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ややっこしいですね！

こういう食塩水を扱う問題のキーポイントは、中に解けている塩の量が

変わらないと言うことです。

５％の食塩水をXｇ、１０％の食塩水をYｇとしますと

X ＋ Y ＝５００ （これは食塩水の重さ）-------①

０．０５X ＋ ０．１０Y ＝ ０．０８×５００ （これは塩の重さ）--------②

として、連立方程式を作って解きます。

Y の代わりに （５００ － X ）を使っても大丈夫！

②の式を左右両辺を１００倍して

５X ＋ １０Y ＝ ８×５００  とすると計算が楽になりますね。

式さえ書ければ、あとは大丈夫！   かな？

 

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

前回の答え

より

高さと、÷２の ２は、約分で消えてしまいますから

上底+下底  の  割合だけが残ります。

□は、４    答え４ｃｍ     です。

 

 

 

早い！カンタン！分数計算方式～

問題を解くときに、何種類もの計算方法があるとき

あなたは、どのような計算方法を使いますか？

 

たとえば次のような問題。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

A,B二つの台形があります。

Aの台形は上底が９ｃｍ、下底が１１ｃｍ、高さ１４ｃｍ

Bの台形は上底が１３ｃｍ、下底が１５ｃｍ、高さ１４ｃｍです。

Aの面積は、Bの面積の何倍でしょう？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんな時は、Aの面積を求めて、次にBの面積を求めて・・・・・・と、

順番に分かるところからコツコツ計算する方法がありますが、

分数を使うと、早くてカンタンです。

 

まず、台形の面積の求め方！覚えてますか？

そして、数値を代入しますと

となります。

ここで、問題をよく見ますと、

と考えますので

この、AとBに 先ほど求めました式を代入しますと

割り算は、逆数のかけ算にします。

ここで、よく見ると分母と分子に同じ数を発見！そして約分します。

約分することで、実際に計算するのは、足し算と簡単な約分だけ！

この計算方法は、これからも出てきます。ラクチンだから覚えてね～

そして、この答えは分数のままでOKです。

小数にすると割り切れませんから、分数のままの方が正確！

 

それでは、次の問題はどうやって計算したら ラクチンでしょうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

C、D 二つの台形があります。

Cは、上底が５ｃｍ、下底が７ｃｍ

Dは、上底が分からず、下底は１０ｃｍ

CとDの高さは同じです。

Cの面積は、Dの面積の７分の６倍あります。

Dの上底は  何ｃｍでしょうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

 

前回の答え：

図を見ていただくと・・・・

 

   はい！同じ形が３つできました。

  こちらも同じ形が３つ！

な～んだ、そうだったのかー

という声が聞こえてきます・・・・・

 

 

 

わがままな、３人兄弟のために！

もうすぐ新学期が始まりますね～

今のうちに 思いっきり遊ばなくっちゃ！

でも、宿題が出た人もいますね～

 

覚えたり、理解したりすることは、

なかなかまとめてできないものです。

日頃から少しずつ鍛えておきましょうね。

 

と言うことで、今回も小学生の問題。

中学生の皆さん、楽勝でしょうが、小学生に教えてあげてくださいね。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

わがままな ３人兄弟がいました。

いつも同じ物をほしがります。

下の図のような変わった形の板状のお菓子がありました。

どのように切れば、３人は同じ形のお菓子を食べられるでしょうか？

（薄いので横から切ることはできません）

        

 

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

前回の問題と答え：

２０１３年の３月２６日に

４人兄弟が、久々に実家に集まりました。

長男は、１３日ごとに実家に帰ると言い

長女は、７日ごとに実家に帰ると言い

次男は、５日ごとに実家に帰ると言い

次女は、１１日ごとに実家に帰ると言いました。

この４人が、次にそろうのは何年の何月何日でしょうか？

 

なかなか会えない兄弟ですが、

５日、７日、１１日、１３日の公倍数を考えますと

５×７×１１×１３＝５００５  で、５００５日後に全員がそろいます。

１年は３６５日、４年に１度の閏年を計算して

次回そろうのは、２０２６年１２月８日

長いですね～

１３年も先ですか・・・・・

この計算は大変なので、インターネット上には、このような日付を自動で計算する

そんなサイトもあります。でも、一度は手書きで計算してみてください。