2次関数と１次関数の 交点を扱う問題は 多々ありますが
いずれも計算に時間がかかる！と言うのが一般的な見方でした。
が、視点を変えると
変化の割合や 切片が １０秒で分かってしまうというお話。
2次式を因数分解するときは、
答えが
（Ｘ ± Ａ ）（Ｘ ± Ｂ ）のカタチになります。
で、どこから考えると分かりやすいか？
を考えます。
たとえば、
掛けて＋３２、足して－１８ の場合は Ａ，Ｂどちらもマイナスですから
Ａ，Ｂ は、 －２ と －１６
掛けて－３６、足して＋５ の場合は 絶対値の大きい方がプラスですから
Ａ，Ｂ は、 ＋９ と －４
いよいよ中学３年生の皆さんは
中学数学の目玉ともいうべきやっかいな項目
因数分解 というものに取り組みますね
この分解という言葉が分かりにくいですね
２次式を因数分解する というのは
この２次式が、どんな因数のかけ算でできたのかを 明らかにする！
という事です。
たとえば、AB＋AC という式は、
Aという因数と B＋C という因数をかけてできたものだということを表しますと
AB＋AC＝A（B＋C） となり 因数分解できたことになります。
またまた続きです
AB と AC の長さが分かったところで
BC の長さを求めます。
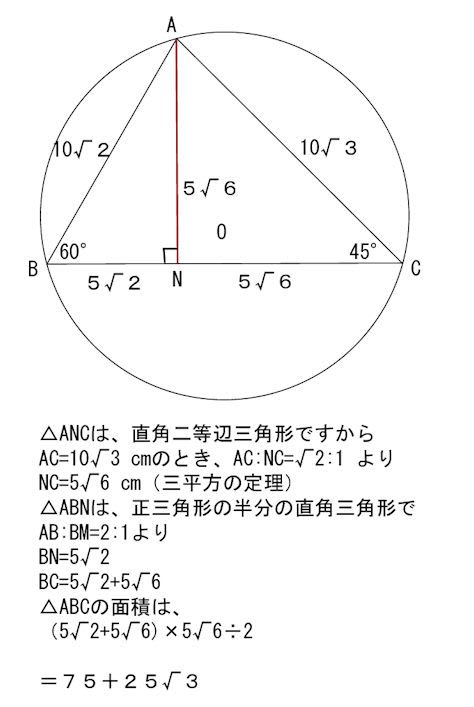
前回の二等辺三角形の中心角を求める方法で
円周角と中心角の関係（円周角×２＝中心角）を使う方法もあります
また、他の方法もあるでしょう。
数学はパズルですから、解き方を考える学問であるような気がします。
推理小説と同じですね。
前回の続きです
円に内接する三角形は、３つの二等辺三角形で構成されていることが分かりました。
今回は、辺の長さを考えます。
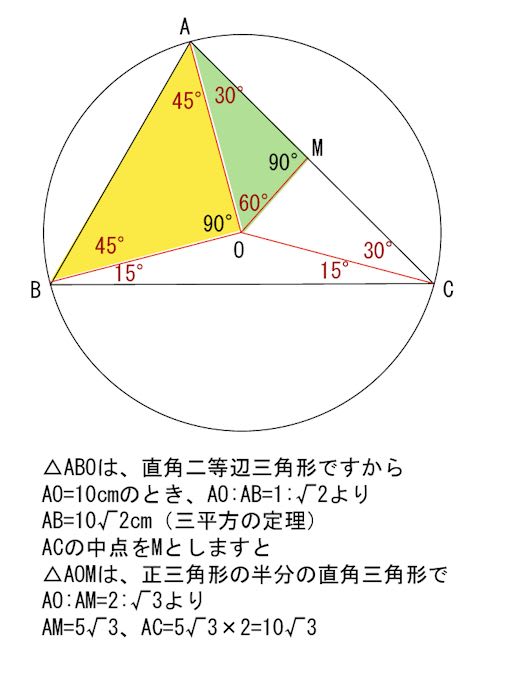
ここまでで、2種類の三角定規が出てきました。
三角定規は、いろんな問題に使われます。
三角定規の辺の長さの比は、暗記しておいた方が便利です。
あと、1辺の長さと 面積については次回に！