正五角形という図形は、
数学の問題の中には ひんぱんに現れます。
とても不思議な図形 五角形。
神秘的な図形でもあります。
ちょっと複雑ですが、コンパスと直線定規だけで描ける図形です。
今回は、角度だけに絞って この正五角形を見てみますと
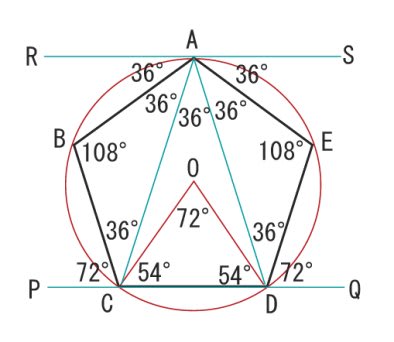
このようになります。 ここで RS//PQ です。
∠CODは、360°の5分の1なので、この角度を計算するときに
ほとんど方は 360÷5 を計算します。
でも、こんな時は 360÷10×2 を計算した方が楽ですね。
△OCDの底角を計算するときも、
この△OCDをタテ半分に分けて、直角三角形を作り
上側の頂角は 360÷10で 36°でしたから 直角以外の残りの角は
90-36 で、54° これなら 暗算でできそうですね。
正五角形の内角は、この底角2つ分ですから 54×2 で 108°
このように 36°と54° 、そしてそれらの2倍の72°と108° が
あちらこちらに出てきます。
ここで前回の問題
これは、正五角形が上下ひっくり返っていますが 考え方は同じ
また、この正五角形は、10°回転していますから
回転しない平行線とは、10°の差が生じます。
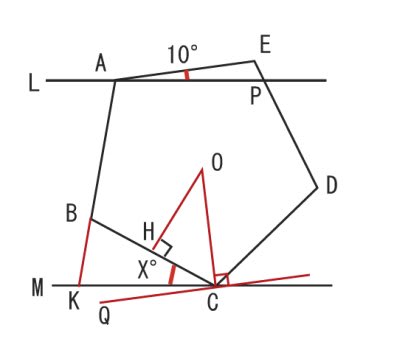
もう お分かりかと思いますが、
10°回転する前は、Xは 36°だったはずです。
でも、10°回転して減ってしまいましたから、Xは、26°
計算の仕方は、無数にあります。
一番早くて確実な方法を見つけ出してください。













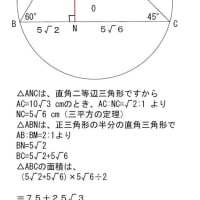
たとえば、点Aに、5つの辺に平行な線を集めてみますと
点Aを中心に角度が10等分された線が現れます。
辺OC、辺ODの 平行線も引きますと
最初に図形の中に現れる角度の同位角が
点Aの周りにあります。
点Aを中心に角度が10等分された線の真ん中に
さらに5本の線を引いて角度を20等分すれば
現れる同位角は、すべて360度の20等分である
18度の倍数になります。
http://cialisbnb.com/# where can u buy cialis