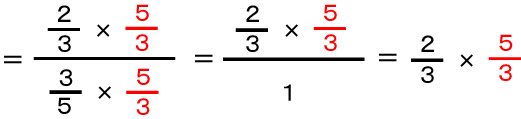円錐の展開図～の巻き

いきなりですが、

次の円錐の展開図で、

扇形の中心角 X の大きさは何度か 分かりますか？

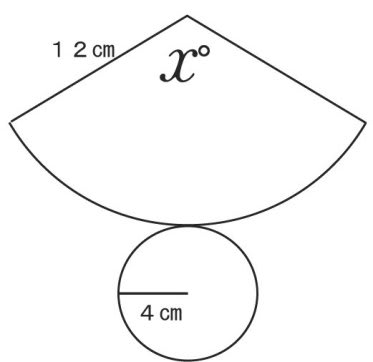
そうです。１２０°ですね～  暗算でできますね～

と、ここで取り残されちゃった人！

大丈夫です。どうして暗算でできちゃうのか？

最後まで読めば、な～んだ  に変わりますから。

 

その前に、円錐（えんすい）って何だか分かりますか？

クリスマスなんかで頭にかぶる先のとんがった帽子

又は、工事現場に置いてある赤いコーン

これが、円錐！

これを切って広げた物が展開図です。

さて、この展開図を見ますと、大きな扇形と小さい円になっています。

扇形の半径をR、円の半径を ｒ 、扇形の中心角を X とします。

この扇形の丸いところ（弧と呼びます）と小さい円の円周が、同じ長さです。

円周は、直径×円周率（パイ）でしたね。

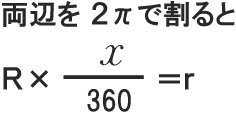
式が短くなりました！

 

分数だけになりました。

 

 

扇形の半径と、円の半径の比が分かれば、

３６０°と中心角 X°の比も、分かるのです。

では、最後に

 

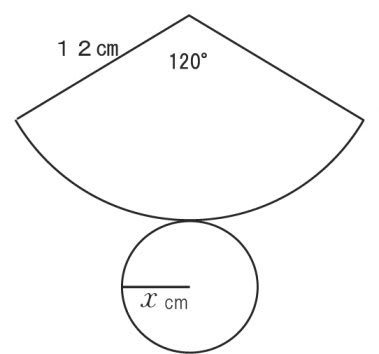
こんな、問題が出てきたら？

１２： X ＝３６０ ： １２０   と考えると、１２： X ＝３：１になりますから、 X＝４

  円の半径は４ｃｍです。

暗算でできましたか？

 

 

入試によく出る三角形！

高校入試も間近ですね～

勉強、進んでますか？

あちゃ～

入試問題で、必ずと言っていいほどよく出る問題に

三平方の定理  が、あります。

ところがこの 三平方の定理 を習うのが

中学３年の後半で、ちょうど今頃という人も多いかと・・・

遅いんですよね～  これじゃあ入試対策問題も解けやしない！

簡単な定理ですから、とっとと覚えてしまえばいいのに、

ということで教室ではずいぶん早くからこの定理の説明をしています。

また、やみくもに勉強したって時間が限られていますから

疲れる割りには、学力が上がらない～ とお困りの方！

問題見てすぐに分からなかったら、解答をみて解き方のパターンを覚えましょう！

誰だって初めて経験する問題には、解決するのに時間がかかるもんです

大事な入試問題を解くときに、じっくり時間なんてかけていられない！

今日は、ちょっとヒントを

入試問題の三平方の定理を使って解く問題によく出る直角三角形ベスト３は、

前回出ました、三角定規２種類と、長さの比が３：４：５の直角三角形。

 

 特に、この３：４：５の三角形は、どの辺も無理数を使わずとも、

見た目も美しく（？）書けるのでよく使われます。

たとえば、次のような問題

 

長方形ABCDの周囲の長さが２８ｃｍで対角線、ACの長さが１０ｃｍの時、

この長方形の面積はいくらか？

本来は、たとえばABを未知数Xとして２次方程式を書いて因数分解して縦と横の長さを

計算してから、面積を計算するという、非常に時間のかかる方法を使いますが、

チョット待てよ、斜辺も周辺も無理数が出てこない！

ひょっとしたら、三角形の辺の比は３：４：５ではなかろうか？と目星をつけると

斜辺が１０になっている。では、６：８：１０かもしれない、ということで周囲の長さを計算すると

６+８+６+８＝２８！  おお！これじゃん！

だったら、面積は６×８＝４８  答え４８ｃｍ2

と、時間短縮、計算カンタン、でミスも減少します。

 

 

 

三角定規のきまり？

三角定規について、知っていることを全部書いてください。

と、言いますと  何項目書けますか？

一つは二等辺三角形で、もう一つは角度が30°と60°のやつ？

なんといいかげんな表現～

でも、日頃意識していない物を表現しようとすると こんなもんです。

で、実はこの三角定規というものは、定規になるための決まりがあります！

どういう事かと言うと、

正三角形の半分と、正四角形の半分のカタチになっています。

   

正三角形って３つの角度は全部同じですね、ではそれぞれ何度？

全部で１８０°だから、ひとつ６０°！

左側の定規は、直角三角形で上が６０°の半分になっているから３０°！

右側の三角定規は、これも直角三角形でしかも二等辺三角形です。

と、ここまでは小学生の範囲！

中学生になりますと、角度以外に辺の長さが重要になってきます。

もう習った人も、まだ習っていない人も、

三角定規で分かることをたくさん覚えましょう！

ところでこの２種類の三角定規を使って作れる角度には

１５°、３０°、４５°、６０°、７５°、９０°、１０５°、１２０°、１３５°、１５０°、１６５°

があります。どうしたら、これらの角度が作れるのか？分かりますか？

（小学生の問題です）

 

 

また、正しい定規は、上の図の赤い線の長さが同じになるように作られています。

昔買った定規は、高かったのですがピッタリあっていました。

最近１００円ショップで買ったものは、あっていませんでした ～(T_T)～

おっとー中学生向けの問題はないのか！って？

それでは、

二つの三角定規の、面積の比は   何 対 何 ？

 

分数の割り算 の マジック～

分数Ａ÷分数Ｂの場合、

分数Ａ×分数Ｂの逆数 となります。

小学校６年生は習っています。

では、どうして逆数をかけるのか？

中学生に聞いても、みなさんよく分からない～

ただ、そうするもんだと教わったから～と答えます。

この謎を説明する方法は、何通りもありますが

たとえば、下記のように書きながら説明しますと

納得はしていただきます。

------------------------------------------

例：  たとえば、次のような問題

これはどうしたら計算できるかというと

まず、分数ではない整数の割り算の場合

と、答えを分数で書くことができます。

これは、一般的に考えますと、

と、なるわけですね。

それでは、最初の問題もこのように考えますと、

と、こんなふうに書けます。

ところが、分数の中に分数があるとわかりにくいので、

この分母を１にすれば分かりやすくなるのでは？

ということで、この式の続きを

分母にあった分数の逆数（分子と分母がひっくり返った分数）を、

分母側にも、分子側にもかけたのです。

おお！そうしますと、最初の割り算が、かけ算に変身しました。

そして、割る数（分数）の逆数をかける式になっています。

 

1回でも、納得した式は、途中の説明を忘れてしまっても、

覚えた方法や、覚えた式に自信が持てます。

 

 

 

間違っていない マチガイ の巻き～

分数の引き算の問題を、一生懸命解いていたＡくんは、

次のような答えを導き出しました

もちろん、これは正解ではないのですが、

ここで、赤ペンで × をつけて返してしまうと重大な問題を見過ごしてしまう事になります。

Ａくんは、どうしてこの答えを出すにいたったのか？

彼の頭の中では、この答えは論理的に導き出されているようなのです。

なぜかと言いますと、迷いがなくこの答えにいたったから、

では、その論理とは何でしょう？

とても気になり、答えが合っているとか間違っているとか言う前に

教えてもらうことにしました。

 

彼が言いますには、

最初の分数の分子は１で、次の分数の分子は２

引き算で、１から２は引けないので

最初の分数は、左横の１を借りてきて１１にして、

１１から２を引けば９、

だから答えは、３ぶんの９！

 

う～～～～～～ん、なるほど～～

 

引けないときは、となりから１借りてきて１０を足してから引き算をするという

筆算の大原則！

彼は、この筆算の大原則を忠実に守った訳です。

ただ、この大原則も分数では使えない事を教わっていなかった！！

そこで、申し訳ないけど、・・・・・とお話ししてこの場合の計算の仕方を納得してもらい

再度同じ問題にチャレンジしてもらって、見事1回で正解に至ったときには

5重の花丸をつけて拍手です！

 

間違いではなく、覚え違い、

 

けっこう多いのです。だから、答えが違っていても

やたらと × をつけてはいけない。教える側の義務です。