９マスパズルの 算数的解決法～

昨日の、９マスのパズルは解けたでしょうか？

なんか、適当に書いてるうちにできちゃった！

という人もいるでしょうね。

でも、適当に書いててもわかんなかった～という人のために

今日は、このようなパズルの解き方、考え方について！

----------------------------------------------------------------

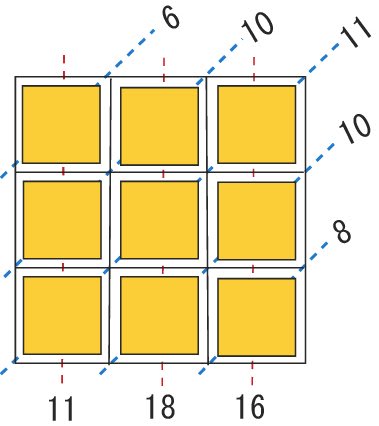
昨日のパズルは、タテとナナメの合計だけが分かっている場合

１～９までのプレートは、どのように並べたのでしょうか？

という問題でした。

このプレートに、Ａ～Ｉ までの名前をつけて説明します。

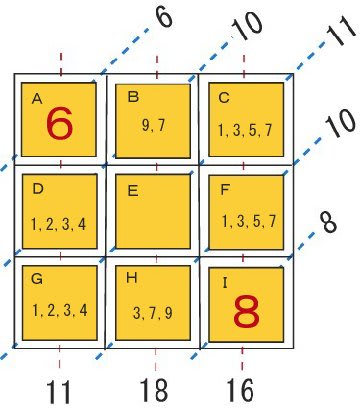
Ａ と Ｉ の数字は、Ａ＝６，Ｉ＝８ と、ナナメの合計より分かります。

あとのプレートは、６，８以外の数字で可能性のある数字を書いてみます。

Ｃ＋Ｆが８になること、Ｄ＋Ｇが５になることより考えて

次にＢとＨの可能性を考えてみましょう。

ここでＢに注目しますと、可能性があるのは、７と９です。

試しに、７を入れてみますと Ｄが３，Ｇが２となり Ｈは９です。

そうするとＦは1で、Ｃは７？７が２回出てくるのでこのパターンはダメ！

それでは、最初に戻って

Ｂは９、としますと  Ｄは１，Ｇは４、Ｈは７、Ｆは３，Ｃは５

そして最後に残った２をＥに入れますとすべての数字が合計と合います。

 

めでたしめでたし～

 

 

小学生でも解ける！９マスパズル

今日はちょっと教科書から離れて

算数のパズルを

--------------------------------------------------------------------

１～９までの数字が書かれた四角いプレートがあります。

これらを、９マスの枠に並べて、

タテの３つの数字の合計を下に書き、

ナナメの数字の合計を図のように書きました。

最後に、数字の書いたプレートを裏返しにしました。

裏返す前の、９つのプレートの数字をあててください。

 

ヒント：使える数字、使えない数字を整理していきましょう！

円錐の 不思議で ビックリな 公式～

以前、１月３１日の記事で紹介しましたが

円錐について、もう少しおさらいを。

                   

        

円錐の体積を求める方法は、

底面積×高さ÷３  で、計算できました。式にしますと

 

でしたので、この a と b に、数字を代入すればできますね。

例えば、a が５，b が３だったら、ルートの部分は４で、分母と b で約分して

残った数は、４×３×π で、１２π。暗算でできますね。

このとき、約分できるときは先に約分する方が計算は簡単になります。

ではでは、

側面積や、表面積は、簡単には分からないぞ！とお考えの方

大丈夫。円錐というのは、実に不思議な物体なのです。

側面積や表面積は、次のような式になります。

 

え～、ほんと？

 

学校で、最初に習ったときは、

まず弧の長さを底面の円周から求めて、

半径 a で書いた円の円周との割合から

中心角を求めて

半径 a の円の面積を求めて、中心角を使った割合をかけて

やっと、側面積（扇形）の面積が分かる・・・・というような方法でした。

   

でもでも、この方法で a と b を使って式を書き、約分して整理しますと

 

となってしまうのです。

びっくりですね～

これを、自分専用の公式として覚えてしまえば

こんなに簡単で楽なことはない！

 

１月３１日の記事、「円錐の展開図～の巻き」もご参照ください。

 

 

短期間で、１００問仕上げるための 禁じ手？

今まで、たくさん勉強してきたにもかかわらず

問題集の問題が、解けない、分からない、

どこから手を付けたらいいのかさえ分からない～

という事はよくあります！

 

これは問題を解くためのパターン が、自分の中になかったから

すぐには分からなかったことでもあります。

ゲームで言えば、攻略法ですかね～

 

だったら、攻略法(パターン）をたくさん見ておけば、分かりやすくなります。

そこでオススメしたいのが、

分からないときは、すぐに解答を見ること！

今まで、すぐに解答を見てはいけない！と教えられてきませんでしたか？

 

問題集や、プリントを自宅で解こうとしますと、やたら時間がかかって

イヤになることがありますが、

分かるところだけ書いて、分からないところはとばします。

あとで分からなかった問題の解答を見て

どのように解いていったらできるのか？を確認します。

確認して納得するまで解答を読んで、分かったら次の解答を見る。

最後に、とばした問題を解答を見ないで解いてみる。

そこで、やはり分からないものはとばして、分かるものだけ解いていく。

この繰り返しで、攻略法を覚えていけば

手が止まることがありません。

常に頭と手が連動して、パターンを覚えていきます。

 

算数数学を、時間をかけてじっくり考えていくパズルとして楽しむのもいいのですが

入試直前の今、より多くのパターン（攻略法）を獲得する方が、

楽しく勉強できるようです。(以前より２０点、アップして自分で驚いている人もいました）

 

慣れてくれば、１時間で１０～２０問の解き方のパターンが分かります。

３日で新たな１００問攻略も、夢ではない！

 

効率の良い勉強の仕方を考えるのも、数学ですよー

折り紙、折れますか～ 中学３年生諸君！

今日は、折り紙の問題、

分からなかったら、適当な紙を正方形に切って

折りながら考えてください。

---------------------------------------------------------

正方形の折り紙を折って

正三角形を作るには

どのように折ればいいでしょう？

さあ、考えよう。

答えは、このずーと下の方に

 

折って

考えて

折って

考えて

折って

考えて

折って

考えて

 

 

 

 

 

それでは、

答えの中のひとつ。

まず横半分に折ります。

それから、折り目にあわせて次のように折ります。

折り目ができたら、いったん広げて反対側も同じように折ります。

これを広げると、正三角形の折り目ができます。

   

ここで、さらに問題！

この折り方で、なぜ正三角形ができるのでしょうか？

そして、この正三角形より大きな正三角形を折るには

どのように折ればいいのでしょうか？

いや～難しいね～   分かったら あんたは偉い！