割り箸の 先に 円形の板をはさんで
その割り箸を くるくる~と回しますと
平面だった円が、球形に見えてきます。
このように平面を ある軸で回転させたときにできる回転体の体積を考えます。
直角三角形で、斜辺以外の辺を軸にして回転させると
三角錐ができます。
この三角錐の体積の求め方は、もう習った方が多いのでは?
とんがり帽子の三角錐の体積は
底面積×高さ÷3 でした。
なぜ 3 で割るのか? ということについては ほとんどの人が習っていません。
教科書には、明記されていなかったように思います。
文章で説明するには複雑ですからね~先送りですね~
(ここで、先送りなんかしないできちんと説明しろ!と叫ぶ学生など
皆無なんでしょうね・・・・・
教室では2種類の模型を作って、立体でせつめいしていますが・・・)
今回は、三角形ではなく、直角三角形を2枚使った平行四辺形を回転させます。
=================================
平行四辺形ABCDで、
辺AD=2cm、DB=4cm、∠ADB=∠CBD=90°の場合、
DBを軸に回転させたときにできる回転体の体積はいくらでしょう?
円周率はπとします。
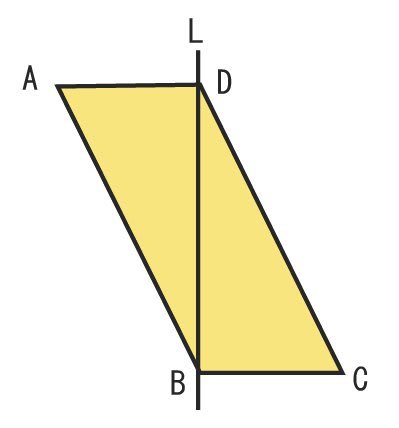

================================
ヒント:真ん中で、2つに切って考えると、分かりやすいかもしれません。
回転体の問題は、数多くあります。どれも円周率は不可欠ですね。
そして、上の問題のように 回転したときの図が描いてある物と
文章だけの問題というのもあります。
図が描いていないものは、自分で描けるようになっていないと
ちょっと大変かも~
次のような文章問題だと、図が描けますか?
同一平面上において、3cm間隔で平行な直線、L,M,N. がある。
L,M,N に垂直な線P とPから3cmの距離でPに平行な直線Qがあるとき
L,M,P,Q で囲まれた正方形が、Nを軸にして回転したときにできる
回転体の体積を求めましょう。










