
原始惑星系円盤のガスが消える前に微惑星が地球質量の10倍以上の岩石惑星成長しないとガス惑星無しの惑星系も多数存在することになる。
木星の4倍質量以上のガス惑星は分子雲から直接形成という筋道が有ることが分かったので遠隔のガス惑星から褐色矮星クラスは有りがち。以下、機械翻訳。
ストリーミングの不安定性と乱流: 微惑星形成の条件
要約
流動不安定性 (SI) は微惑星形成の有力な候補であり、ガスとの双方向の空気力学的相互作用によって固体が濃縮される可能性があります。 得られた濃度
粒子の自己重力下で崩壊するほど高密度になる可能性があり、微惑星を形成します。
前の研究では、臨界粒子対ガス表面密度を確立するために大規模なパラメータ調査が実施されています。
比率 (Z)、これを超えると SI に起因する濃度が微惑星形成を引き起こします。 閾値Z
無次元停止時間 (τs、ダスト サイズの代理) に依存します。 しかし、これらの研究では粒子の自己重力と外部乱流の両方が無視されています。 ここでは3D層状せん断ボックスを実行します
粒子の自己重力と乱流強制力の両方を使用したシミュレーション。これを αD によって特徴付けます。
乱流の拡散を測定します。 我々は、強制乱流が、おそらくいくつかの振幅で存在していることを発見しました。
原始惑星系円盤では、しきい値 Z が最大 1 桁増加する可能性があります。 たとえば、
τs = 0.01、微惑星形成は、αD = 10^−4 、10^−3.5、そして10^−3で Z ≳ 0.06、≳ 0.1、≳ 0.2 のときに発生します。
それぞれ。 αD と τs の関数として臨界 Z への単一の適合を提供します。
SI が機能します (ただし、τs = 0.01 ~ 0.1 の範囲に限定されます)。 私たちのシミュレーションでも、微惑星が
形成には、臨界値を持つ 1 を超える粒子対ガス密度比の中央面が必要です。
αDから独立しています。 最後に、以下を考慮した粒子スケール高さの推定を提供します。
粒子フィードバックと外部乱流の両方。
キーワード: 惑星形成 (1241)、原始惑星系円盤 (1300)、流体力学 (1963)、流体力学シミュレーション (767)、微惑星 (1259)
1. はじめに
惑星の形成には、小さな塵粒子の衝突から星周円盤内の巨大な惑星の移動に至るまで、さまざまな物理的プロセスが含まれます。
それは効率的かつ迅速でなければなりません。 その成長が必要です
ミクロンサイズの塵から本格的な惑星まで
規模が 10^5 km までは、ガスが消散するまでに数百万年以内に完了する可能性があり、示唆されているようにさらに早く完了する可能性があります。
いくつかの観察による(例:Manara et al. 2018、Segura Cox et al. 2020)。 プロセスの中間段階では、ミリメートルからセンチメートルサイズの小石が合体してキロメートルスケールの微惑星が形成されますが、次のいずれかを伴います。
答えるのが最も難しい質問: どのようにして
微惑星は、はるかに小さい小石の構成要素から形成されます (最近のレビューについては、Simon et al. 2022 を参照)。
この質問に答える際の課題は、
形成するために克服しなければならない成長の障壁
微惑星。 まず、衝突凝固中に
ダスト粒子は、〜mm〜のサイズの粒子を生成するのに効果的です。
cm、このスケールを超える成長は断片化および/またはバウンスによって停滞します。後者はさらに
断片化限界に達しても成長を防ぎます (Zsom他。 2010年、詳細については Dominik & Dullemond 2023 も参照
最近の作品)。 内部領域にあるこれらのより大きな粒子の
(≲ 10 au) の原始惑星系円盤 (PPD; 例: Blum &ワーム 2008; グトラーら。 2010年; ゾムら。 2010年; バーン・スティールら。 2012)。 第二に、粒子は次のような軌道を経験します。
ケプラー速度が速いと、彼らは逆風を感じます。
よりゆっくりと回転するサブケプラー気体。 この逆風
粒子から角運動量を取り除き、それらは半径方向内側に向かって流れます。 ドリフトタイムスケール以来
ディスクの寿命に比べて短い(例えば、50 AU で cm サイズの粒子の場合、〜 300 またはバイタル周期; 安達他。 1976)、急速な半径方向のドリフトにより、
外側領域での粒子の成長 (Birnstiel et al.2012)。
これらの成長の障壁は、ストリーミングの不安定性によって回避できます (SI、Youdin & Goodman 2005)。
ガス間の角運動量交換から生じる
空気力学的カップリングを介して固体粒子を生成します。 線形
SI の研究 (Youdin & Goodman 2005; Youdin & Johansen 2007) は、結合していることを実証しました。
円盤内の気固体系は不安定であり、指数関数的な成長率は主に無次元に依存します。
粒子の停止時間 (τs) と粒子とガスの密度比。 数値シミュレーションは、線形領域を超えて、SI の非線形進化が進むことを示しています。
粒子が細いフィラメントに集中しているため、
状況によっては、これらのフィラメントが到達する可能性があります。
十分に高密度になると重力崩壊が起こり、微惑星が形成されます (Johansen et al. 2007, 2009;
ヨハンセンら。 2015年; サイモンら。 2016年; シュアーファーら。2017年; アボードら。 2019)。
いくつかの数値研究がその性質を詳しく調べてきました
の臨界比を調べることによる SI 凝集の
小石の表面密度とガスの表面密度 (Z) の関係は、それを超えると SI が強い凝集を引き起こし、微惑星の形成を促進します。
これらの研究は、(τs, Z) パラメータ空間 (Carrera) 内の広い領域を調査しました。
他。 2015年; ヤンら。 2017年; リー&ユーディン 2021、以下
LY21)、これら 2 つの組み合わせを決定する境界 (「凝集境界」) を定量化します。
パラメータを使用すると、強い凝集が発生する可能性があります。 彼らは持っている
最も低い臨界 Z 値が付近で発生することを確認しました。
τs 〜 0.1 - 0.3、正確な臨界 Z 値は依存します
特定の数値設定 (垂直境界など)
条件とドメインのサイズ。 Li & Youdin 2021、セクション 4.1.4 を参照)。 SI 凝集のしきい値は次のとおりです。
パラメータ空間の大部分について確立されているものとして、
より現実的な物理学の存在下でこの境界を理解するには、まだ作業が必要です。
粒子の自己重力と外部乱流。
まず、以前の SI シミュレーションでは (駆動) 時間がかかりませんでした。
外部乱気流1
考慮に入れてください。 観測ショー
PPD は、それに比べて乱流が弱いものの、
完全に電離した降着円盤の予測では、円盤間で実質的に異なるゼロではないレベルの乱流の証拠があります。 乱流の観測
広がりは乱流速度の上限を導き出します
HD 163296 では音速比 δv/cs 〜 0.01 (Fla herty et al. 2017; 他のディスクについては Flaherty et al. 2018 および Fla herty et al. 2020 も参照)、他のディスクでは
(DM Tau – Flaherty et al. 2020 および IM Lup – Paneque Carre˜no et al. 2023) は、1 ~ 2H で δv/cs 〜 0.3 を示しています (Hガスの垂直スケール高さ)は、中央平面から離れています。 鉛直沈下に敏感な観測
塵粒子の存在は、より弱い乱流を示唆しています。
クラス II ディスクのミッドプレーン (つまり、δv/cs ≲ 0.003)
Oph163131 ディスクの外側領域(ターンオーバーを想定)
局所軌道に似た乱流渦のタイムスケール
タイムスケール。 ビルナベら。 2022)、またはクラス I 円盤のより穏やかな乱流 (例: 外側の δv/cs ≳ 0.01)
同じ仮定の下での IRAS04302 ディスクの領域
売上高のタイムスケールについて、τs = 0.01 と仮定します。 ヴィル・レナーヴら。 2023年)。 明らかに乱気流の強さ
(少なくともこれらの観察から推測されるように) ディスク間では異なります。 したがって、私たちが理解することが重要です
SI 凝集基準に対する乱流の影響、および
微惑星形成、SI 自体が設定した最小値から少なくとも
DM Tau および IM Lup で推定されるレベル。
第二に、凝集境界に関する以前の研究では、
粒子の自己重力は無視され、微惑星形成のしきい値は代わりに次のように定義されます。
最大粒子密度がヒル密度を超えるかどうか (よくこの条件と呼ばれます)
「強い凝集」。 LY21)。 非常に弱い乱気流が存在する場合(たとえば、
SI 自体によって生成されたものと同様)、ヒル基準は次のとおりです。
おそらく崩壊の十分な条件です。 粒子雲
狭いフィラメント内での(つまり、局所的な粒子の過密度)
潮汐に対して安定するには十分な密度が必要です
剪断。 しかし、乱流が重要になる場合、粒子雲を自重で崩壊させるには、重力が潮汐剪断だけでなく拡散も圧倒しなければなりません。
したがって、乱流拡散と潮汐せん断の両方が起こり得るので、
自己重力に対抗するため、重力不安定性に関するトゥームレのような基準が崩壊のより適切な基準となり、拡散が同様の役割を果たします。
圧力 (Gerbig et al. 2020; Klahr & Schreiber 2020;Gerbig & Li 2023)。
これらの考慮事項は、包含を強く動機付けるものです
外部乱流と粒子自己重力の両方の
凝集境界を決定します。 したがって、この論文では、粒子の自己重力と
乱流を 3D ガスと粒子の数値シミュレーションに強制的に導入します。 ここでは次のように定義される凝集境界を定量化するために、41 回のシミュレーションを実行します。
重力で束縛された塊がその上にある境界
私たちのシミュレーションでフォームを作成します。
我々は、これまでの多くの研究が乱流の影響下での粒子の集中と微惑星の形成に取り組んでいることに注目します。 例えば、
Chen & Lin (2020) および Umurhan 他。 (2020) 中程度の乱気流であっても分析的に示す
(すなわち、αSS ≳ 10^−4
; ここで、αSS は標準シャクラ スニャエフ乱流粘度パラメーターです。 Shaakura & Sun yaev 1973) は、SI の線形成長を抑制することができます。 の
乱流が SI を妨げる可能性があるという考えは、外部から駆動される流体力学的乱流を使用した非線形 SI シミュレーションによって数値的に確認されました (Gole et al. 2020)。
さらに、(磁気)によって引き起こされる乱流の影響を調査する研究が数多く行われています。
)PPD に存在する流体力学的不安定性(以下のような)
MRI (Johansen et al. 2007; Yang et al. 2018; Xu &Bai 2022a)または垂直せん断不安定性(VSI; Nelson et al. 2013; については Schâfer & Johansen 2022 を参照)
VSI および SI 研究)、粒子濃度について。
これらの研究から得られる主な点は、粒子の集中が大規模な特徴(局所的な構造など)で発生する可能性があるということです。
ガス圧の濃度)が自然に発生する
作動中の(磁気)流体力学プロセスから。
これらの結果については後ほど説明します。
この原稿ですが、今のところ言及する価値があるのは、
これらの数値研究は、τs と Z に関してパラメータ空間の比較的狭い領域を調査しました。
乱気流の影響はまだ明らかにされていません。
より広いパラメータ空間。 そのようなパラメータを調べる
乱流(および粒子の自己重力)のある空間は、この論文の目標。
本稿は以下のように構成されている。 私たちの
数値的アプローチについてはセクション 2 で説明します。セクション 3.1 では、
粒子濃度に対する乱流の影響を調べます。 セクション 3.2 では、次のシミュレーションについて説明します。
粒子の自己重力が含まれます。 したがって、このセクションでは、新しい凝集境界を提示します。 セクションで粒子フィードバックの効果を示します。
3.3 および粒子密度の垂直プロファイルに対するその影響についてはセクション 3.4 で説明します。 最後に議論してまとめます
結果はそれぞれセクション 4 と 5 で説明します。

図 1. シミュレーションにおける Λ と αD の関係
τs = 0.1、Z = 10^−5の場合。 前者は初期条件です
強制振幅の場合は (式 12)、後者は
パラメータ (式 13) は、SI シミュレーションで乱流のレベルを示すために使用します。 このプロットに示されている Λ 値
は線形補間によって得られます (詳細については本文を参照してください)。 それぞれの赤い水平線は、選択した各 αD を示します。
10^−4、10^−3.5、10^−3。 誤差バーは±1標準を示します
偏差。 補間された Λ 値が次の結果になることを確認します。
希望するαD値を高精度で実現します。

図 2. 上: シミュレーションにおけるガスの実効速度 (黒) と粒子の最大密度 (オレンジ) の時間変化
τs = 0.1、Z = 0.02。 中央: 領域 z/H ∈ [−0.1, 0.1] にズームインした方位角平均粒子密度 (側面図)。
下: 垂直に積分された粒子質量密度 (つまり、粒子の表面密度、Σp、上面図)。 スナップショットが取得されます
t−tpar = 350Ω^−1の場合
。 中央と下部のパネルのカラーバー スケールが異なることに注意してください。 左から右へ、強制せずに、
αD = 10^−4、10^−3.5、10^−3
実行が表示されます。 上部の各パネルの水平線は、ヒル密度を示します (式 10 を参照)。
ここで紹介する実行では、パーティクルの自己重力は無効になっています。 乱流が左から右に強くなるにつれて、粒子層は
太くなり、フィラメントはより拡散し、明確でなくなります。

図 3. 実行を「崩壊」または「崩壊なし」として分類するための概念実証。 左: 最大粒子の時間発展
T10Z2A35 (緑) および T10Z3.2A35 (青) 実行の密度。 水平線と垂直線はヒル密度と tsg を示します。
それぞれ。 中央: T10Z2A3.5 実行時の Σp の空間平均で割った最終スナップショット。 右: 中央パネルと同じ
ただし、T10Z3.2A3.5の場合は実行します。 青色で示されているように最大密度が大幅に増加した場合、実行を「崩壊」と定義します。
左側のパネルに曲線が表示され、2D スナップショットに境界オブジェクト (つまり、図に示すように非常に小さなスケールでの強い過密度) が表示される場合は、
右パネル)。
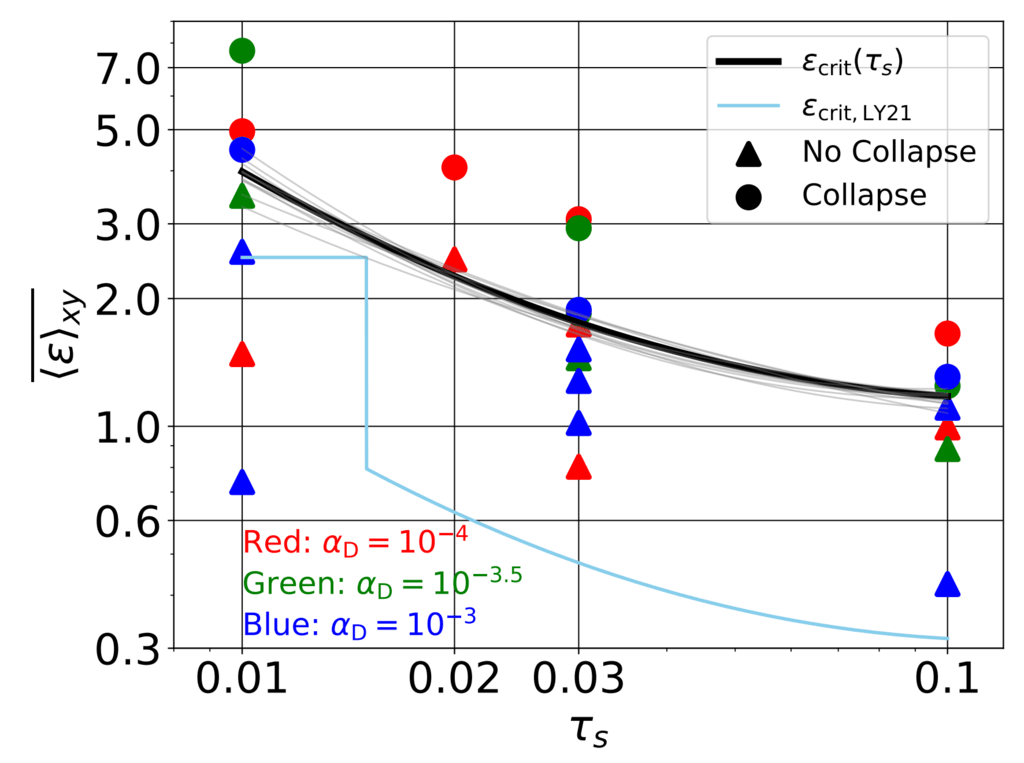
図 4. τs の関数として表した、中間面での粒子密度とガス密度の時間的および水平方向の平均比
私たちのシミュレーション。 凝集前の段階が短すぎて時間平均を取ることができないシミュレーションは含まれていません。 どこで実行しますか
崩壊が発生したものは円で示され、崩壊が発生しなかったものは三角形で示されています。 赤、緑、
と青は αD = 10^−4 、10^−3.5、10^−3を表します
、それぞれ、Z 値を示しませんでした。 黒い曲線は、
式 (16) で説明されているように、最小二乗は ϵ の臨界値に最も良く適合します。 薄い灰色の曲線は、
最適曲線の不確実性を示す A、B、C の多変量正規分布 (式 16)。 も含まれます
LY21 の臨界曲線。空色の曲線 (ϵcrit,LY21) として示されます。 この図は、ϵcrit が αD によって変化しないことを示しています (つまり、
αD を変更すると、すべての非崩壊ケースがすべての崩壊ケースを下回ります)、その結果、すべての ϵ 値に適合する単一の臨界曲線が得られます。
αD関係なく。

図 5. 表 1 にリストされている SI シミュレーションにおける重力崩壊の概要 (ただし、強制を行わない T10Z2 の実行を除く)
適用済み。 崩壊が発生したランは黒丸で表示され、崩壊が発生しなかったランは黒丸で表示されます。
開いた円として。 左から右へ、αD = 10^−4、10^−3.5、10^−3、 それぞれ。 各パネルに、2 つの異なる Zcrit、スカイブルーをプロットします。
は式 (17)、赤は式 (19) です。 どちらの曲線も臨界 Z 値に適合していますが、異なる値を使用しています。
アプローチ。 赤い曲線は多変量最小二乗法により最もよく適合します (式 19 が式を示します)。一方、空色の曲線は
は、式 (16) の ϵcrit を使用して、粒子密度の垂直プロファイルがガウスであると仮定して臨界 Z を計算します。
各パネルの薄い灰色の曲線は、A' 、B'、C'、D'の多変量正規分布から抽出されたランダム フィットです。
(方程式19) 不確実性に基づく値(本文を参照)。 したがって、これらの曲線は Zcrit 曲線の不確実性を表します。 毎
ここで示されている実行は Π = 0.05 および Ĝ= 0.05 (または Q 〜 32) です。 Zcrit(τs, αD) は τs と の範囲で使用する必要があることを強調します。
αDは式(19)で与えられます。 外部乱流がない場合、τs = 0.01 の臨界 Z 値が 〜 0.02 であるとすると (例:
LY21)、外部乱流により臨界値が大幅に増加します。 Zcrit(τs = 0.01, αD) 〜 0.06、〜 0.1、〜 0.2 (αD = 10^−4 、10^−3.5、10^−3の場合)
、 それぞれ。 Zcrit(τs, αD) の 3D インタラクティブ バージョンは、https://jhlim.weebly.com/research.html で入手できます。

図 6. z (Σp) で積分され、y (⟨Σp⟩y) で平均化された粒子密度の時空間プロット。 数量をプロットします
vs.xと時間。 上から下に、それぞれ τs = 0.01、0.02、0.03 です。 実行の Z と αD は同じで、0.04 です。
そして10^−4、 それぞれ。 ここで考慮されている期間中、パーティクルの自己重力はオフになります。 フィラメントは頻繁に
十分に密度が高くないと破壊され、3 つの τ 値すべてが確率的に進化します。

図 7. 図 4 と同様ですが、粒子の垂直位置の時間平均標準偏差 (式 20) が示されています。
ガススケールの高さの単位。 各パネルの黒い破線は、説明されている粒子スケールの高さの予測を示しています。
式(18)で。 図 4 と同様に、十分な長い時間内で時間平均を実行できるシミュレーションのみを示します。
凝集前の段階。 シミュレーションで測定された標準偏差は常に予測よりも低くなります。

図 8. 図 7 と同様ですが、σp,z と He の時間平均比 (式 21)。 からの結果は報告しません。
プレクランピング段階が短すぎるシミュレーション (図 7 など)。 この図は、τs = 0.01 でのいくつかの実行を除いて、
この比は、与えられた αD におけるすべての τ の破線 (式 18) とよく一致します。

図 9. x および y で平均化された粒子密度 (⟨ρp⟩xy) 対 z および時間 (左) および時間平均された粒子密度の時空間プロット
τs = 0.01 での 3 回の実行における粒子密度の垂直プロファイル (右) は、式 (23) から逸脱した σp,z を示しています。 粒子
ここで考慮されている期間中、自己重力はオフです。 上から下まで、αD = 10^−4、10^−3.5、10^−3。 左側のパネルでは、
水平破線は、右側のパネルに示されている Voigt プロファイルの FWHM を示しています。 実線、破線、点線
右側のパネルの は、それぞれシミュレーション データ、ガウス フィット、データへのフォークト フィットを示します。 の各パネルのタイトル
右は、各プロファイルが平均化される時間間隔を示します。 z = ±0.4H の間の分布のみを示していることに注意してください。
一方、実際の計算ボックスの垂直方向の範囲はこの領域を超えています。 粒子は周囲に薄くて緻密な層を形成します
中央平面にあり、ガウス分布から大幅に逸脱した垂直方向の密度プロファイルを持ちます。

図 10. 図 9 と同様ですが、τs = 0.1、Z = 0.02 です。 z = ±0.2H と do の間の分布を示していることに注意してください。
Voigt が正しいパネルに収まる様子は表示されません。ここで示されている期間中、粒子の自己重力はオフになっています。 τs = 0.01 の場合とは異なり、
薄くて緻密な層は形成されず、垂直方向のプロファイルはガウスに近くなります。

図 11. 有効粒子解像度 (np,eff ) 以外のすべてのパラメーターを同じにした 2 つのシミュレーションの比較。 の
左のパネルは、最大粒子密度の時間変化を示しています。黒と灰色の曲線は基準に対するものです。
実行 (Run T10Z2A4, np,eff 〜 8) および Run T10Z2A3 の実効解像度での実行 (Run T10Z2A4-np, np,eff 〜 8)、
それぞれ。 オレンジ色の水平線はヒル密度 (ρH) です。 中央と右のパネルは時空プロットを示しています。
粒子密度を y で平均し、z 対 x および 2 回の実行の時間を積分しました。 ここではパーティクルの自己重力は無効になっています。
最大密度と半径方向濃度にわずかな違いがあるにもかかわらず、異なる np,eff を使用した 2 つの実行は非常に似ています。

図 12. 上空の粒子雲の臨界半径
どの崩壊が起こるか (rcrit; 式 26) は次の関数として発生します。
τs のδ = 0.01 (青)、0.03 (緑)、0.1 (赤)。 左側と右側の y 軸は rcrit/Δ と rcrit/H を示します。
ここで、Δはグリッドセルの幅です。 想定します
δ ≈ αD,z、範囲は 10^−6 ~ 4×10^−4。
この範囲内の大きい数値は、αD = 10^−3の値に対応します。
、小さい数字は想定値に基づくものです。
粒子が密集した周囲では拡散が弱くなるという事実
固まる。 黒い水平線はΔを表します。 を除いて、
δ が非常に小さい場合、臨界半径はセルのサイズ。
5. 概要
この論文では、ガスと粒子が存在する層状せん断ボックスのシミュレーションの結果を紹介しました。
相互に空気力学的に結合されています。 するために
流れ不安定性 (SI) と微惑星の形成に対する乱流の影響を研究するには、以下のものが含まれます。
粒子の自己重力と外部駆動の両方
非圧縮乱流。 私たちのシミュレーションでは、
比較的広い範囲のパラメータ空間、つまり、異なる無次元停止時間 τs、粒子からガスまで
表面密度比 Z、および強制振幅 αD。 私たちは
主な結果を次のように要約します。
1. 非圧縮性乱流は SI 駆動を妨げる可能性があります
乱流拡散による粒子の集中
考えられる2つの方法で。 まず、この拡散により粒子の沈降が防止され、それによって粒子の沈降が防止されます。
ミッドプレーンの塵とガスの密度比 ϵ がフィラメント形成の臨界値を超えないようにします。 第二に、たとえ粒子が沈降して層を形成したとしても
ミッドプレーンの周囲では、フィラメントの形成が可能です。
乱流拡散作用によって平衡が保たれる
(垂直に加えて) ディスクの平面内でも。
2. 微惑星形成が起こる限界値 ϵ は、ϵ ≳ 1 です。これは数倍の係数です。
外部からの乱気流が存在しない場合の対応する値よりも大きくなりますが、それでも
秩序の統一。
3. に関連する強力な拡散のバランスをとるため
αD が大きいほど、粒子内の総質量が大きくなります (つまり、Z パラメータを介して) が必要です。 そのため、
惑星の形成が起こる臨界 Z 値 (Zcrit) 以上は、それよりもはるかに高い
外部乱流なしで得られます。 定量的には、τs = 0.01 の場合、Zcrit 〜 0.06 および 〜 0.2
αD = 10^−4 および 10^−3 の場合、それぞれ、一方 微惑星の形成には Z 〜 0.02 で十分です
乱気流がない場合(LY21など)。
4. 粒子フィードバックにより、シミュレーションにおける粒子の特徴的な高さ (σp,z) は常に低くなります。
粒子スケールの高さよりも高く、フィードバックは無視できます。 この動作は、ガス上の粒子質量負荷が増大したことの直接の結果です。
5. ダストスケールの高さに対する粒子フィードバックの強い影響の結果として、乱流速度の観測測定は下限として考慮される必要があります。 可能です
より強い乱流と小さなダストスケールの高さ
塵とガスの比率が十分に大きい場合。
6. Z が十分に大きい場合、垂直方向の粒子密度プロファイルは、
ガウス。 τs = 0.01 および Z ≥ Zcrit の場合、シミュレーションではミッドプレーン近くにカスプが表示され、次の結果が得られます。
薄くて緻密な粒子の層で、拡張された
層の外側の翼、フォークトのプロフィールに似ている
|z| へ ≲ 0.2H。
最後に、まだ不確実な点がいくつかありますが、
将来の研究で対処する必要があることを私たちの結果が示しています
ガス乱流が制限において果たす重要な役割
円盤のどこに、どのような条件下で小惑星が形成されるのか。

図A.1。 シミュレーションで粒子を初期化する前の乱流速度の 2 乗の時間平均パワー スペクトル
(Lx、Ly、Lz) = (0.4、0.2、0.8)H。 凡例に示すように、3 つの αD 値が異なる色で示されています。 黒の破線
線はコルモゴロフ依存性を表します (∝ k^−5/3)。 パワースペクトルには、kH/(2π) 〜 10 にピークがあり、その後にべき乗則が続きます。
波数が大きくなる傾向にあり、これはエネルギー カスケードの兆候である可能性があります。
木星の4倍質量以上のガス惑星は分子雲から直接形成という筋道が有ることが分かったので遠隔のガス惑星から褐色矮星クラスは有りがち。以下、機械翻訳。
ストリーミングの不安定性と乱流: 微惑星形成の条件
要約
流動不安定性 (SI) は微惑星形成の有力な候補であり、ガスとの双方向の空気力学的相互作用によって固体が濃縮される可能性があります。 得られた濃度
粒子の自己重力下で崩壊するほど高密度になる可能性があり、微惑星を形成します。
前の研究では、臨界粒子対ガス表面密度を確立するために大規模なパラメータ調査が実施されています。
比率 (Z)、これを超えると SI に起因する濃度が微惑星形成を引き起こします。 閾値Z
無次元停止時間 (τs、ダスト サイズの代理) に依存します。 しかし、これらの研究では粒子の自己重力と外部乱流の両方が無視されています。 ここでは3D層状せん断ボックスを実行します
粒子の自己重力と乱流強制力の両方を使用したシミュレーション。これを αD によって特徴付けます。
乱流の拡散を測定します。 我々は、強制乱流が、おそらくいくつかの振幅で存在していることを発見しました。
原始惑星系円盤では、しきい値 Z が最大 1 桁増加する可能性があります。 たとえば、
τs = 0.01、微惑星形成は、αD = 10^−4 、10^−3.5、そして10^−3で Z ≳ 0.06、≳ 0.1、≳ 0.2 のときに発生します。
それぞれ。 αD と τs の関数として臨界 Z への単一の適合を提供します。
SI が機能します (ただし、τs = 0.01 ~ 0.1 の範囲に限定されます)。 私たちのシミュレーションでも、微惑星が
形成には、臨界値を持つ 1 を超える粒子対ガス密度比の中央面が必要です。
αDから独立しています。 最後に、以下を考慮した粒子スケール高さの推定を提供します。
粒子フィードバックと外部乱流の両方。
キーワード: 惑星形成 (1241)、原始惑星系円盤 (1300)、流体力学 (1963)、流体力学シミュレーション (767)、微惑星 (1259)
1. はじめに
惑星の形成には、小さな塵粒子の衝突から星周円盤内の巨大な惑星の移動に至るまで、さまざまな物理的プロセスが含まれます。
それは効率的かつ迅速でなければなりません。 その成長が必要です
ミクロンサイズの塵から本格的な惑星まで
規模が 10^5 km までは、ガスが消散するまでに数百万年以内に完了する可能性があり、示唆されているようにさらに早く完了する可能性があります。
いくつかの観察による(例:Manara et al. 2018、Segura Cox et al. 2020)。 プロセスの中間段階では、ミリメートルからセンチメートルサイズの小石が合体してキロメートルスケールの微惑星が形成されますが、次のいずれかを伴います。
答えるのが最も難しい質問: どのようにして
微惑星は、はるかに小さい小石の構成要素から形成されます (最近のレビューについては、Simon et al. 2022 を参照)。
この質問に答える際の課題は、
形成するために克服しなければならない成長の障壁
微惑星。 まず、衝突凝固中に
ダスト粒子は、〜mm〜のサイズの粒子を生成するのに効果的です。
cm、このスケールを超える成長は断片化および/またはバウンスによって停滞します。後者はさらに
断片化限界に達しても成長を防ぎます (Zsom他。 2010年、詳細については Dominik & Dullemond 2023 も参照
最近の作品)。 内部領域にあるこれらのより大きな粒子の
(≲ 10 au) の原始惑星系円盤 (PPD; 例: Blum &ワーム 2008; グトラーら。 2010年; ゾムら。 2010年; バーン・スティールら。 2012)。 第二に、粒子は次のような軌道を経験します。
ケプラー速度が速いと、彼らは逆風を感じます。
よりゆっくりと回転するサブケプラー気体。 この逆風
粒子から角運動量を取り除き、それらは半径方向内側に向かって流れます。 ドリフトタイムスケール以来
ディスクの寿命に比べて短い(例えば、50 AU で cm サイズの粒子の場合、〜 300 またはバイタル周期; 安達他。 1976)、急速な半径方向のドリフトにより、
外側領域での粒子の成長 (Birnstiel et al.2012)。
これらの成長の障壁は、ストリーミングの不安定性によって回避できます (SI、Youdin & Goodman 2005)。
ガス間の角運動量交換から生じる
空気力学的カップリングを介して固体粒子を生成します。 線形
SI の研究 (Youdin & Goodman 2005; Youdin & Johansen 2007) は、結合していることを実証しました。
円盤内の気固体系は不安定であり、指数関数的な成長率は主に無次元に依存します。
粒子の停止時間 (τs) と粒子とガスの密度比。 数値シミュレーションは、線形領域を超えて、SI の非線形進化が進むことを示しています。
粒子が細いフィラメントに集中しているため、
状況によっては、これらのフィラメントが到達する可能性があります。
十分に高密度になると重力崩壊が起こり、微惑星が形成されます (Johansen et al. 2007, 2009;
ヨハンセンら。 2015年; サイモンら。 2016年; シュアーファーら。2017年; アボードら。 2019)。
いくつかの数値研究がその性質を詳しく調べてきました
の臨界比を調べることによる SI 凝集の
小石の表面密度とガスの表面密度 (Z) の関係は、それを超えると SI が強い凝集を引き起こし、微惑星の形成を促進します。
これらの研究は、(τs, Z) パラメータ空間 (Carrera) 内の広い領域を調査しました。
他。 2015年; ヤンら。 2017年; リー&ユーディン 2021、以下
LY21)、これら 2 つの組み合わせを決定する境界 (「凝集境界」) を定量化します。
パラメータを使用すると、強い凝集が発生する可能性があります。 彼らは持っている
最も低い臨界 Z 値が付近で発生することを確認しました。
τs 〜 0.1 - 0.3、正確な臨界 Z 値は依存します
特定の数値設定 (垂直境界など)
条件とドメインのサイズ。 Li & Youdin 2021、セクション 4.1.4 を参照)。 SI 凝集のしきい値は次のとおりです。
パラメータ空間の大部分について確立されているものとして、
より現実的な物理学の存在下でこの境界を理解するには、まだ作業が必要です。
粒子の自己重力と外部乱流。
まず、以前の SI シミュレーションでは (駆動) 時間がかかりませんでした。
外部乱気流1
考慮に入れてください。 観測ショー
PPD は、それに比べて乱流が弱いものの、
完全に電離した降着円盤の予測では、円盤間で実質的に異なるゼロではないレベルの乱流の証拠があります。 乱流の観測
広がりは乱流速度の上限を導き出します
HD 163296 では音速比 δv/cs 〜 0.01 (Fla herty et al. 2017; 他のディスクについては Flaherty et al. 2018 および Fla herty et al. 2020 も参照)、他のディスクでは
(DM Tau – Flaherty et al. 2020 および IM Lup – Paneque Carre˜no et al. 2023) は、1 ~ 2H で δv/cs 〜 0.3 を示しています (Hガスの垂直スケール高さ)は、中央平面から離れています。 鉛直沈下に敏感な観測
塵粒子の存在は、より弱い乱流を示唆しています。
クラス II ディスクのミッドプレーン (つまり、δv/cs ≲ 0.003)
Oph163131 ディスクの外側領域(ターンオーバーを想定)
局所軌道に似た乱流渦のタイムスケール
タイムスケール。 ビルナベら。 2022)、またはクラス I 円盤のより穏やかな乱流 (例: 外側の δv/cs ≳ 0.01)
同じ仮定の下での IRAS04302 ディスクの領域
売上高のタイムスケールについて、τs = 0.01 と仮定します。 ヴィル・レナーヴら。 2023年)。 明らかに乱気流の強さ
(少なくともこれらの観察から推測されるように) ディスク間では異なります。 したがって、私たちが理解することが重要です
SI 凝集基準に対する乱流の影響、および
微惑星形成、SI 自体が設定した最小値から少なくとも
DM Tau および IM Lup で推定されるレベル。
第二に、凝集境界に関する以前の研究では、
粒子の自己重力は無視され、微惑星形成のしきい値は代わりに次のように定義されます。
最大粒子密度がヒル密度を超えるかどうか (よくこの条件と呼ばれます)
「強い凝集」。 LY21)。 非常に弱い乱気流が存在する場合(たとえば、
SI 自体によって生成されたものと同様)、ヒル基準は次のとおりです。
おそらく崩壊の十分な条件です。 粒子雲
狭いフィラメント内での(つまり、局所的な粒子の過密度)
潮汐に対して安定するには十分な密度が必要です
剪断。 しかし、乱流が重要になる場合、粒子雲を自重で崩壊させるには、重力が潮汐剪断だけでなく拡散も圧倒しなければなりません。
したがって、乱流拡散と潮汐せん断の両方が起こり得るので、
自己重力に対抗するため、重力不安定性に関するトゥームレのような基準が崩壊のより適切な基準となり、拡散が同様の役割を果たします。
圧力 (Gerbig et al. 2020; Klahr & Schreiber 2020;Gerbig & Li 2023)。
これらの考慮事項は、包含を強く動機付けるものです
外部乱流と粒子自己重力の両方の
凝集境界を決定します。 したがって、この論文では、粒子の自己重力と
乱流を 3D ガスと粒子の数値シミュレーションに強制的に導入します。 ここでは次のように定義される凝集境界を定量化するために、41 回のシミュレーションを実行します。
重力で束縛された塊がその上にある境界
私たちのシミュレーションでフォームを作成します。
我々は、これまでの多くの研究が乱流の影響下での粒子の集中と微惑星の形成に取り組んでいることに注目します。 例えば、
Chen & Lin (2020) および Umurhan 他。 (2020) 中程度の乱気流であっても分析的に示す
(すなわち、αSS ≳ 10^−4
; ここで、αSS は標準シャクラ スニャエフ乱流粘度パラメーターです。 Shaakura & Sun yaev 1973) は、SI の線形成長を抑制することができます。 の
乱流が SI を妨げる可能性があるという考えは、外部から駆動される流体力学的乱流を使用した非線形 SI シミュレーションによって数値的に確認されました (Gole et al. 2020)。
さらに、(磁気)によって引き起こされる乱流の影響を調査する研究が数多く行われています。
)PPD に存在する流体力学的不安定性(以下のような)
MRI (Johansen et al. 2007; Yang et al. 2018; Xu &Bai 2022a)または垂直せん断不安定性(VSI; Nelson et al. 2013; については Schâfer & Johansen 2022 を参照)
VSI および SI 研究)、粒子濃度について。
これらの研究から得られる主な点は、粒子の集中が大規模な特徴(局所的な構造など)で発生する可能性があるということです。
ガス圧の濃度)が自然に発生する
作動中の(磁気)流体力学プロセスから。
これらの結果については後ほど説明します。
この原稿ですが、今のところ言及する価値があるのは、
これらの数値研究は、τs と Z に関してパラメータ空間の比較的狭い領域を調査しました。
乱気流の影響はまだ明らかにされていません。
より広いパラメータ空間。 そのようなパラメータを調べる
乱流(および粒子の自己重力)のある空間は、この論文の目標。
本稿は以下のように構成されている。 私たちの
数値的アプローチについてはセクション 2 で説明します。セクション 3.1 では、
粒子濃度に対する乱流の影響を調べます。 セクション 3.2 では、次のシミュレーションについて説明します。
粒子の自己重力が含まれます。 したがって、このセクションでは、新しい凝集境界を提示します。 セクションで粒子フィードバックの効果を示します。
3.3 および粒子密度の垂直プロファイルに対するその影響についてはセクション 3.4 で説明します。 最後に議論してまとめます
結果はそれぞれセクション 4 と 5 で説明します。

図 1. シミュレーションにおける Λ と αD の関係
τs = 0.1、Z = 10^−5の場合。 前者は初期条件です
強制振幅の場合は (式 12)、後者は
パラメータ (式 13) は、SI シミュレーションで乱流のレベルを示すために使用します。 このプロットに示されている Λ 値
は線形補間によって得られます (詳細については本文を参照してください)。 それぞれの赤い水平線は、選択した各 αD を示します。
10^−4、10^−3.5、10^−3。 誤差バーは±1標準を示します
偏差。 補間された Λ 値が次の結果になることを確認します。
希望するαD値を高精度で実現します。

図 2. 上: シミュレーションにおけるガスの実効速度 (黒) と粒子の最大密度 (オレンジ) の時間変化
τs = 0.1、Z = 0.02。 中央: 領域 z/H ∈ [−0.1, 0.1] にズームインした方位角平均粒子密度 (側面図)。
下: 垂直に積分された粒子質量密度 (つまり、粒子の表面密度、Σp、上面図)。 スナップショットが取得されます
t−tpar = 350Ω^−1の場合
。 中央と下部のパネルのカラーバー スケールが異なることに注意してください。 左から右へ、強制せずに、
αD = 10^−4、10^−3.5、10^−3
実行が表示されます。 上部の各パネルの水平線は、ヒル密度を示します (式 10 を参照)。
ここで紹介する実行では、パーティクルの自己重力は無効になっています。 乱流が左から右に強くなるにつれて、粒子層は
太くなり、フィラメントはより拡散し、明確でなくなります。

図 3. 実行を「崩壊」または「崩壊なし」として分類するための概念実証。 左: 最大粒子の時間発展
T10Z2A35 (緑) および T10Z3.2A35 (青) 実行の密度。 水平線と垂直線はヒル密度と tsg を示します。
それぞれ。 中央: T10Z2A3.5 実行時の Σp の空間平均で割った最終スナップショット。 右: 中央パネルと同じ
ただし、T10Z3.2A3.5の場合は実行します。 青色で示されているように最大密度が大幅に増加した場合、実行を「崩壊」と定義します。
左側のパネルに曲線が表示され、2D スナップショットに境界オブジェクト (つまり、図に示すように非常に小さなスケールでの強い過密度) が表示される場合は、
右パネル)。

図 4. τs の関数として表した、中間面での粒子密度とガス密度の時間的および水平方向の平均比
私たちのシミュレーション。 凝集前の段階が短すぎて時間平均を取ることができないシミュレーションは含まれていません。 どこで実行しますか
崩壊が発生したものは円で示され、崩壊が発生しなかったものは三角形で示されています。 赤、緑、
と青は αD = 10^−4 、10^−3.5、10^−3を表します
、それぞれ、Z 値を示しませんでした。 黒い曲線は、
式 (16) で説明されているように、最小二乗は ϵ の臨界値に最も良く適合します。 薄い灰色の曲線は、
最適曲線の不確実性を示す A、B、C の多変量正規分布 (式 16)。 も含まれます
LY21 の臨界曲線。空色の曲線 (ϵcrit,LY21) として示されます。 この図は、ϵcrit が αD によって変化しないことを示しています (つまり、
αD を変更すると、すべての非崩壊ケースがすべての崩壊ケースを下回ります)、その結果、すべての ϵ 値に適合する単一の臨界曲線が得られます。
αD関係なく。

図 5. 表 1 にリストされている SI シミュレーションにおける重力崩壊の概要 (ただし、強制を行わない T10Z2 の実行を除く)
適用済み。 崩壊が発生したランは黒丸で表示され、崩壊が発生しなかったランは黒丸で表示されます。
開いた円として。 左から右へ、αD = 10^−4、10^−3.5、10^−3、 それぞれ。 各パネルに、2 つの異なる Zcrit、スカイブルーをプロットします。
は式 (17)、赤は式 (19) です。 どちらの曲線も臨界 Z 値に適合していますが、異なる値を使用しています。
アプローチ。 赤い曲線は多変量最小二乗法により最もよく適合します (式 19 が式を示します)。一方、空色の曲線は
は、式 (16) の ϵcrit を使用して、粒子密度の垂直プロファイルがガウスであると仮定して臨界 Z を計算します。
各パネルの薄い灰色の曲線は、A' 、B'、C'、D'の多変量正規分布から抽出されたランダム フィットです。
(方程式19) 不確実性に基づく値(本文を参照)。 したがって、これらの曲線は Zcrit 曲線の不確実性を表します。 毎
ここで示されている実行は Π = 0.05 および Ĝ= 0.05 (または Q 〜 32) です。 Zcrit(τs, αD) は τs と の範囲で使用する必要があることを強調します。
αDは式(19)で与えられます。 外部乱流がない場合、τs = 0.01 の臨界 Z 値が 〜 0.02 であるとすると (例:
LY21)、外部乱流により臨界値が大幅に増加します。 Zcrit(τs = 0.01, αD) 〜 0.06、〜 0.1、〜 0.2 (αD = 10^−4 、10^−3.5、10^−3の場合)
、 それぞれ。 Zcrit(τs, αD) の 3D インタラクティブ バージョンは、https://jhlim.weebly.com/research.html で入手できます。

図 6. z (Σp) で積分され、y (⟨Σp⟩y) で平均化された粒子密度の時空間プロット。 数量をプロットします
vs.xと時間。 上から下に、それぞれ τs = 0.01、0.02、0.03 です。 実行の Z と αD は同じで、0.04 です。
そして10^−4、 それぞれ。 ここで考慮されている期間中、パーティクルの自己重力はオフになります。 フィラメントは頻繁に
十分に密度が高くないと破壊され、3 つの τ 値すべてが確率的に進化します。

図 7. 図 4 と同様ですが、粒子の垂直位置の時間平均標準偏差 (式 20) が示されています。
ガススケールの高さの単位。 各パネルの黒い破線は、説明されている粒子スケールの高さの予測を示しています。
式(18)で。 図 4 と同様に、十分な長い時間内で時間平均を実行できるシミュレーションのみを示します。
凝集前の段階。 シミュレーションで測定された標準偏差は常に予測よりも低くなります。

図 8. 図 7 と同様ですが、σp,z と He の時間平均比 (式 21)。 からの結果は報告しません。
プレクランピング段階が短すぎるシミュレーション (図 7 など)。 この図は、τs = 0.01 でのいくつかの実行を除いて、
この比は、与えられた αD におけるすべての τ の破線 (式 18) とよく一致します。

図 9. x および y で平均化された粒子密度 (⟨ρp⟩xy) 対 z および時間 (左) および時間平均された粒子密度の時空間プロット
τs = 0.01 での 3 回の実行における粒子密度の垂直プロファイル (右) は、式 (23) から逸脱した σp,z を示しています。 粒子
ここで考慮されている期間中、自己重力はオフです。 上から下まで、αD = 10^−4、10^−3.5、10^−3。 左側のパネルでは、
水平破線は、右側のパネルに示されている Voigt プロファイルの FWHM を示しています。 実線、破線、点線
右側のパネルの は、それぞれシミュレーション データ、ガウス フィット、データへのフォークト フィットを示します。 の各パネルのタイトル
右は、各プロファイルが平均化される時間間隔を示します。 z = ±0.4H の間の分布のみを示していることに注意してください。
一方、実際の計算ボックスの垂直方向の範囲はこの領域を超えています。 粒子は周囲に薄くて緻密な層を形成します
中央平面にあり、ガウス分布から大幅に逸脱した垂直方向の密度プロファイルを持ちます。

図 10. 図 9 と同様ですが、τs = 0.1、Z = 0.02 です。 z = ±0.2H と do の間の分布を示していることに注意してください。
Voigt が正しいパネルに収まる様子は表示されません。ここで示されている期間中、粒子の自己重力はオフになっています。 τs = 0.01 の場合とは異なり、
薄くて緻密な層は形成されず、垂直方向のプロファイルはガウスに近くなります。

図 11. 有効粒子解像度 (np,eff ) 以外のすべてのパラメーターを同じにした 2 つのシミュレーションの比較。 の
左のパネルは、最大粒子密度の時間変化を示しています。黒と灰色の曲線は基準に対するものです。
実行 (Run T10Z2A4, np,eff 〜 8) および Run T10Z2A3 の実効解像度での実行 (Run T10Z2A4-np, np,eff 〜 8)、
それぞれ。 オレンジ色の水平線はヒル密度 (ρH) です。 中央と右のパネルは時空プロットを示しています。
粒子密度を y で平均し、z 対 x および 2 回の実行の時間を積分しました。 ここではパーティクルの自己重力は無効になっています。
最大密度と半径方向濃度にわずかな違いがあるにもかかわらず、異なる np,eff を使用した 2 つの実行は非常に似ています。

図 12. 上空の粒子雲の臨界半径
どの崩壊が起こるか (rcrit; 式 26) は次の関数として発生します。
τs のδ = 0.01 (青)、0.03 (緑)、0.1 (赤)。 左側と右側の y 軸は rcrit/Δ と rcrit/H を示します。
ここで、Δはグリッドセルの幅です。 想定します
δ ≈ αD,z、範囲は 10^−6 ~ 4×10^−4。
この範囲内の大きい数値は、αD = 10^−3の値に対応します。
、小さい数字は想定値に基づくものです。
粒子が密集した周囲では拡散が弱くなるという事実
固まる。 黒い水平線はΔを表します。 を除いて、
δ が非常に小さい場合、臨界半径はセルのサイズ。
5. 概要
この論文では、ガスと粒子が存在する層状せん断ボックスのシミュレーションの結果を紹介しました。
相互に空気力学的に結合されています。 するために
流れ不安定性 (SI) と微惑星の形成に対する乱流の影響を研究するには、以下のものが含まれます。
粒子の自己重力と外部駆動の両方
非圧縮乱流。 私たちのシミュレーションでは、
比較的広い範囲のパラメータ空間、つまり、異なる無次元停止時間 τs、粒子からガスまで
表面密度比 Z、および強制振幅 αD。 私たちは
主な結果を次のように要約します。
1. 非圧縮性乱流は SI 駆動を妨げる可能性があります
乱流拡散による粒子の集中
考えられる2つの方法で。 まず、この拡散により粒子の沈降が防止され、それによって粒子の沈降が防止されます。
ミッドプレーンの塵とガスの密度比 ϵ がフィラメント形成の臨界値を超えないようにします。 第二に、たとえ粒子が沈降して層を形成したとしても
ミッドプレーンの周囲では、フィラメントの形成が可能です。
乱流拡散作用によって平衡が保たれる
(垂直に加えて) ディスクの平面内でも。
2. 微惑星形成が起こる限界値 ϵ は、ϵ ≳ 1 です。これは数倍の係数です。
外部からの乱気流が存在しない場合の対応する値よりも大きくなりますが、それでも
秩序の統一。
3. に関連する強力な拡散のバランスをとるため
αD が大きいほど、粒子内の総質量が大きくなります (つまり、Z パラメータを介して) が必要です。 そのため、
惑星の形成が起こる臨界 Z 値 (Zcrit) 以上は、それよりもはるかに高い
外部乱流なしで得られます。 定量的には、τs = 0.01 の場合、Zcrit 〜 0.06 および 〜 0.2
αD = 10^−4 および 10^−3 の場合、それぞれ、一方 微惑星の形成には Z 〜 0.02 で十分です
乱気流がない場合(LY21など)。
4. 粒子フィードバックにより、シミュレーションにおける粒子の特徴的な高さ (σp,z) は常に低くなります。
粒子スケールの高さよりも高く、フィードバックは無視できます。 この動作は、ガス上の粒子質量負荷が増大したことの直接の結果です。
5. ダストスケールの高さに対する粒子フィードバックの強い影響の結果として、乱流速度の観測測定は下限として考慮される必要があります。 可能です
より強い乱流と小さなダストスケールの高さ
塵とガスの比率が十分に大きい場合。
6. Z が十分に大きい場合、垂直方向の粒子密度プロファイルは、
ガウス。 τs = 0.01 および Z ≥ Zcrit の場合、シミュレーションではミッドプレーン近くにカスプが表示され、次の結果が得られます。
薄くて緻密な粒子の層で、拡張された
層の外側の翼、フォークトのプロフィールに似ている
|z| へ ≲ 0.2H。
最後に、まだ不確実な点がいくつかありますが、
将来の研究で対処する必要があることを私たちの結果が示しています
ガス乱流が制限において果たす重要な役割
円盤のどこに、どのような条件下で小惑星が形成されるのか。

図A.1。 シミュレーションで粒子を初期化する前の乱流速度の 2 乗の時間平均パワー スペクトル
(Lx、Ly、Lz) = (0.4、0.2、0.8)H。 凡例に示すように、3 つの αD 値が異なる色で示されています。 黒の破線
線はコルモゴロフ依存性を表します (∝ k^−5/3)。 パワースペクトルには、kH/(2π) 〜 10 にピークがあり、その後にべき乗則が続きます。
波数が大きくなる傾向にあり、これはエネルギー カスケードの兆候である可能性があります。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます