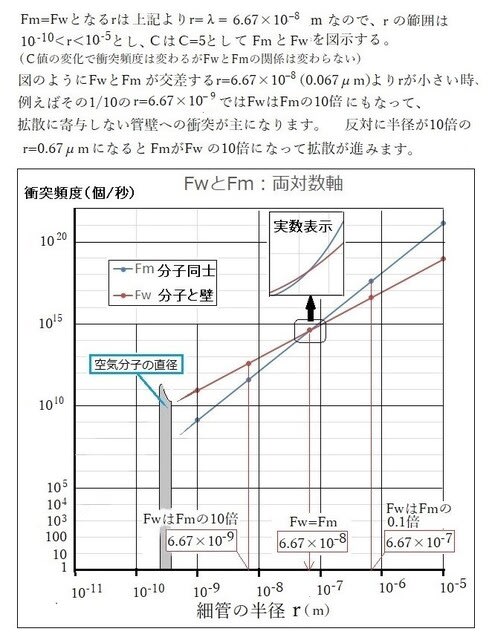
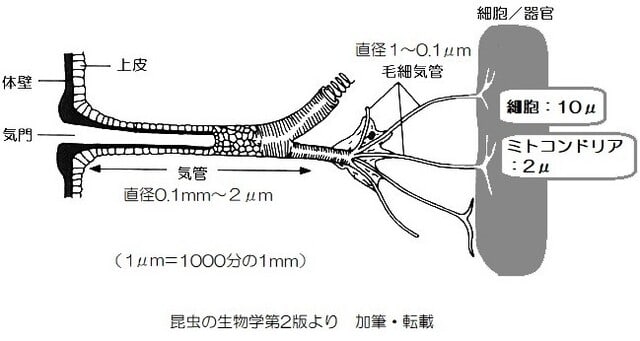
昆虫の呼吸-9
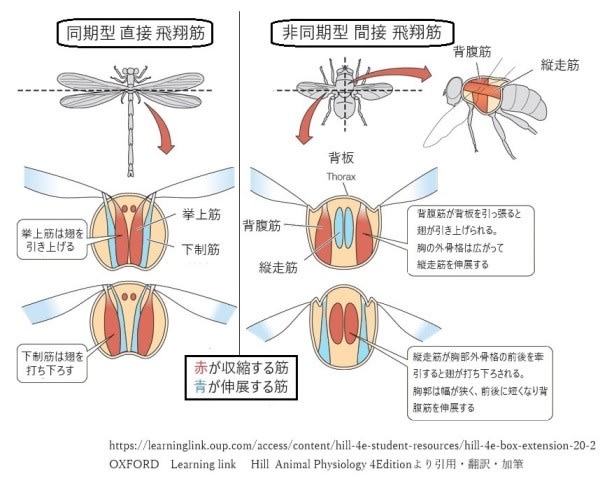
前回、昆虫の飛翔は鳥とは違って外骨格の強靱性や弾力性が重要な役割を果たしていることがわかりました。
強靭といえば、コブゴミムシダマシ科の甲虫は「悪魔の鋼鉄武装甲虫」とも言われ、車に轢かれても潰れないほどですが、その強さは丈夫な材料を繋ぎ合わせる構造に由来していると報告されています(2020年Nature)。
昆虫は飛翔する以外に、バッタ、コオロギ、ノミ、などのように体長の何十倍もの高さに跳ねます。外骨格の強靱性を調べるために、バッタを例にして跳ねる脚の負担についてみてみます。
まず、外骨格の構造ですが、表皮の外側(外表皮)に200μm(0.2mm)以上の厚さを持つキチン質+タンパク質の層があって、その内側には薄い層状のタンパク質とキチンが積み重なっています。これらが外骨格(クチクラ)を形成しています。
構造物に用いられる材料の強度はヤング率で評価されます。ヤング率は材料にかかった力をその力で生じた歪みで割った値(=力/歪み)であり、ケヤキやチークなどの堅い木材では11~13GPa(ギガパスカル)、コンクリート30GPa、一般の鋼材200GPaなどです。(なお、1GPaは1平方mmに約100Kgの圧力を表します)
私たちの骨のヤング率:30GPaはコンクリートと同程度で、昆虫の外皮:クチクラのヤング率:11GPaは木材のケヤキと同程度です。昆虫はこの強靱な材料で胸郭や脚の外骨格を作って、その内側の腔に筋肉や腱を付けて飛翔や跳躍をしています。
○ショウリョウバッタ(キチキチバッタ)が飛び跳ね、着地するときの衝撃について
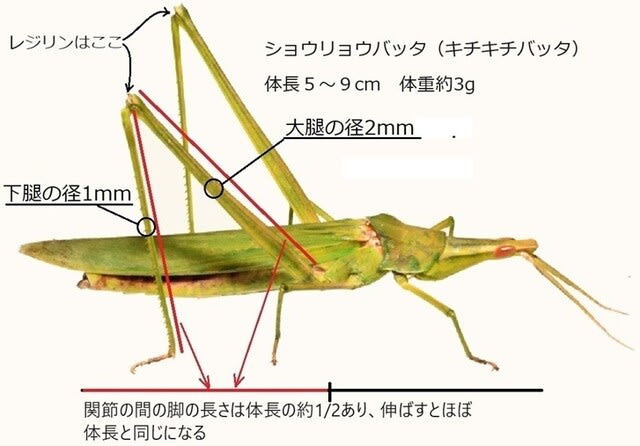 子供の頃に野原でキチキチと音を立てて飛んでいたバッタです。よく捕まえました。このバッタをモデルにして考えてみます。
子供の頃に野原でキチキチと音を立てて飛んでいたバッタです。よく捕まえました。このバッタをモデルにして考えてみます。
バッタの膝関節にはレジリンというゴム状のタンパク質の靱帯があって、これは着地で曲げた時に蓄えたエネルギーの98%を跳ぶときに使えるという優れた効率を持つ弾性体です。
以下の数式に出てくる^の印は累乗を表し、 A^2ならAの2乗です
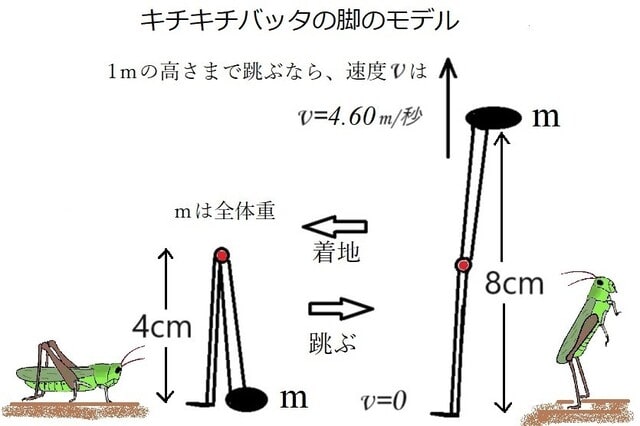
体長8cm、体重3g、伸ばしたときの脚の長さ8cmのバッタが、地面に止まっていて、そこから膝を伸ばして脚底が1mの高さまで跳び上がるとします。
その速度vは、
E=1/2 mv^(2 )=mgh
より、 v=√2gh
h=1.08m g=9.8m/s2 なので、
v=√2gh=4.6m/s
となります。
この速度を得るためには、脚関節のレジリンのエネルギーを使ってL=8cmの高さまで等加速度αでt時間かかるとすると、脚にかかる力Fは
F=mv/t であり、
v=αt 、 L=1/(2 ) αt^(2 ) より t=2L/v なので
F=(1/2 mv^(2 ) )・1/L=mgh/L となる
L=0.08m、m=0.003kg、h=1.08mを代入して
t=0.035秒、 F=0.397N(=0.04kg重)
(Nは力の単位でニュートン、1kg重=9.8N)
つまり、脚が伸びるまでの35マイクロ秒の間、両脚(特に下腿)には40gの重さがかかることになります(体重3gの13倍も!)。
逆に、1mの高さから落ちてくるときには、脚から着地して同じように等加速度で減速すると、やはり40gの重さがかかります。
〇バッタの脚が耐えられる限界の重さは?
バッタの大腿と下腿は、跳ぶときや着地の時の衝撃力に耐えられるように出来ています。脚の外骨格構造を図のような円筒としてモデル化して、脚が耐えられる重さを計算してみます。柱が上からの力(荷重)が大きいと折れ曲がってしまうことを座屈といい、その荷重を座屈荷重といい、それを算出します。
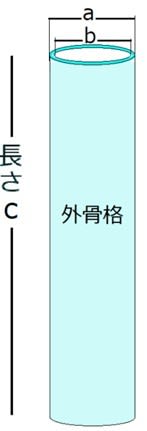 この円筒の青い壁がクチクラです。クチクラの壁の厚さを200μm(0.2mm)とすると、大腿部の直径が2mmだったので、a=2mm、b=1.6mm、 下腿部ではa=1mm、b=0.6mm、どちらも長さC=4cmです。
この円筒の青い壁がクチクラです。クチクラの壁の厚さを200μm(0.2mm)とすると、大腿部の直径が2mmだったので、a=2mm、b=1.6mm、 下腿部ではa=1mm、b=0.6mm、どちらも長さC=4cmです。
クチクラのヤング率Y=11GPaはケヤキと同じなので、この太さと長さの木材の細長比による中空円筒の計算式(オイラーの理論式)を適用します。
材料工学より座屈荷重Pは、
P=(π^3 Y)/64・((a^4-b^4 ))/C^2
となります。
上記のa、b、cとYを代入すると、
大腿部の座屈荷重Pは P=31.4N(=3.2kg重)、下腿部の座屈荷重Pは P=2.89N(=0.3kg重)となり、両脚では600gになりました。
3gのバッタが1mの高さの高さに跳び上がるときに両脚には40gの力がかかりましたが、バッタの脚は細い下腿でも600gの荷重に耐えるので、15倍の安全率です。
なんと自分の体重3gの200倍に耐えられるのです!
○巨大な昆虫の怪獣の運動能力は?
では映画やアニメに出てくるような巨大な昆虫の場合についてみてみます。
上記のバッタがあの形のまま50倍に相似形で大きくになると、体長0.08mx50=4m、 大腿の太さが0.002m×50=10cm、下腿は5cmの太さ、伸ばした脚の長さは4m、体重は50の3乗倍になるので、0.003kg×50x50x50=375kgとなります。
この4mの怪獣が1mの高さまで飛び上がったり、その後に着地したりするときの衝撃力は前と同じ様に計算すると
F=mgh/L m=375kg ,h=5m,L=4m, を代入して
F=4594N(=約469kg重) になります
座屈荷重Pは50の2乗倍になるので P=2.9N×50x50=7250N(=740kg重)
となります。二本脚で約1480kgです。ジャンプの時の脚の強度の安全率は
1480÷469=3.2 と3倍ほどに低下してしまいます。
また、4mの高さにジャンプする時の衝撃はh=8mより、750Kg になるので、片足だと折れ曲がってしまうことになります。これでは、走ったりジャンプしたりしながら戦うことはできそうもありません。
ちなみに100倍になると 体長8m、体重3000kgになり、座屈荷重は2900kg重なので片脚で立つと折れてしまうので、歩くこともできなくなります。
こうしてみると、巨大な怪獣になるにはバッタのようにスマートな体型の外骨格では無理で、クチクラを分厚くして、太めの体型にならないと難しいようです。

(材料工学には素人なので、適切な評価方法のために色々勉強していたので、時間がかかってしまいました。 評価方法に誤りがあればご指摘ください。)
参考文献
1小峯龍男 ゼロからわかる材料力学 技術評論社 東京 2020
2高久田和夫 生体組織の力学-序説 download 2023/11/7
http://www.jsdp.org/kaobio/journal/11/11-1.pdf
3田中英一 皮質骨の力学特性と損傷のモデル化 マテリア 46:460-63 2007
4高嶋聰 クチクラに基づく材料設計論 download 2023/11/10
https://invbrain.neuroinf.jp/modules/htmldocs/IVBPF/Engineering
/Insect_kutikura.html?ml_lang=ja
5「押しつぶされない」コブゴミムシダマシの秘密 download 2023/11/10 Nature2020/10/22https://www.natureasia.com/ja-jp/nature/pr-highlights/13485
6本川達夫 ゾウの時間ネズミの時間 中公新書 1992
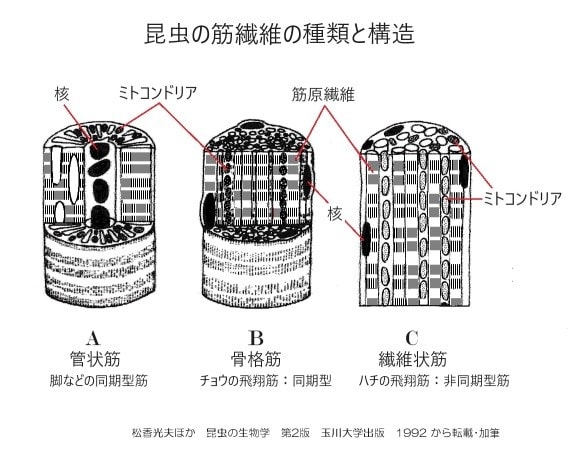
7松香光夫ほか 昆虫の生物学 第2版 玉川大学出版 1992
8Wikipediaより バッタの図
9AmvitionのYouTube動画より昆虫怪獣カマキラスの画像download 2023/12/20 https://www.youtube.com/watch?v=_Er4Mtsd9x8
前回、昆虫の飛翔は鳥とは違って外骨格の強靱性や弾力性が重要な役割を果たしていることがわかりました。
強靭といえば、コブゴミムシダマシ科の甲虫は「悪魔の鋼鉄武装甲虫」とも言われ、車に轢かれても潰れないほどですが、その強さは丈夫な材料を繋ぎ合わせる構造に由来していると報告されています(2020年Nature)。
昆虫は飛翔する以外に、バッタ、コオロギ、ノミ、などのように体長の何十倍もの高さに跳ねます。外骨格の強靱性を調べるために、バッタを例にして跳ねる脚の負担についてみてみます。
まず、外骨格の構造ですが、表皮の外側(外表皮)に200μm(0.2mm)以上の厚さを持つキチン質+タンパク質の層があって、その内側には薄い層状のタンパク質とキチンが積み重なっています。これらが外骨格(クチクラ)を形成しています。
構造物に用いられる材料の強度はヤング率で評価されます。ヤング率は材料にかかった力をその力で生じた歪みで割った値(=力/歪み)であり、ケヤキやチークなどの堅い木材では11~13GPa(ギガパスカル)、コンクリート30GPa、一般の鋼材200GPaなどです。(なお、1GPaは1平方mmに約100Kgの圧力を表します)
私たちの骨のヤング率:30GPaはコンクリートと同程度で、昆虫の外皮:クチクラのヤング率:11GPaは木材のケヤキと同程度です。昆虫はこの強靱な材料で胸郭や脚の外骨格を作って、その内側の腔に筋肉や腱を付けて飛翔や跳躍をしています。
○ショウリョウバッタ(キチキチバッタ)が飛び跳ね、着地するときの衝撃について
 子供の頃に野原でキチキチと音を立てて飛んでいたバッタです。よく捕まえました。このバッタをモデルにして考えてみます。
子供の頃に野原でキチキチと音を立てて飛んでいたバッタです。よく捕まえました。このバッタをモデルにして考えてみます。バッタの膝関節にはレジリンというゴム状のタンパク質の靱帯があって、これは着地で曲げた時に蓄えたエネルギーの98%を跳ぶときに使えるという優れた効率を持つ弾性体です。

以下の数式に出てくる^の印は累乗を表し、 A^2ならAの2乗です
体長8cm、体重3g、伸ばしたときの脚の長さ8cmのバッタが、地面に止まっていて、そこから膝を伸ばして脚底が1mの高さまで跳び上がるとします。
その速度vは、
E=1/2 mv^(2 )=mgh
より、 v=√2gh
h=1.08m g=9.8m/s2 なので、
v=√2gh=4.6m/s
となります。
この速度を得るためには、脚関節のレジリンのエネルギーを使ってL=8cmの高さまで等加速度αでt時間かかるとすると、脚にかかる力Fは
F=mv/t であり、
v=αt 、 L=1/(2 ) αt^(2 ) より t=2L/v なので
F=(1/2 mv^(2 ) )・1/L=mgh/L となる
L=0.08m、m=0.003kg、h=1.08mを代入して
t=0.035秒、 F=0.397N(=0.04kg重)
(Nは力の単位でニュートン、1kg重=9.8N)
つまり、脚が伸びるまでの35マイクロ秒の間、両脚(特に下腿)には40gの重さがかかることになります(体重3gの13倍も!)。
逆に、1mの高さから落ちてくるときには、脚から着地して同じように等加速度で減速すると、やはり40gの重さがかかります。
〇バッタの脚が耐えられる限界の重さは?
バッタの大腿と下腿は、跳ぶときや着地の時の衝撃力に耐えられるように出来ています。脚の外骨格構造を図のような円筒としてモデル化して、脚が耐えられる重さを計算してみます。柱が上からの力(荷重)が大きいと折れ曲がってしまうことを座屈といい、その荷重を座屈荷重といい、それを算出します。
 この円筒の青い壁がクチクラです。クチクラの壁の厚さを200μm(0.2mm)とすると、大腿部の直径が2mmだったので、a=2mm、b=1.6mm、 下腿部ではa=1mm、b=0.6mm、どちらも長さC=4cmです。
この円筒の青い壁がクチクラです。クチクラの壁の厚さを200μm(0.2mm)とすると、大腿部の直径が2mmだったので、a=2mm、b=1.6mm、 下腿部ではa=1mm、b=0.6mm、どちらも長さC=4cmです。クチクラのヤング率Y=11GPaはケヤキと同じなので、この太さと長さの木材の細長比による中空円筒の計算式(オイラーの理論式)を適用します。
材料工学より座屈荷重Pは、
P=(π^3 Y)/64・((a^4-b^4 ))/C^2
となります。
上記のa、b、cとYを代入すると、
大腿部の座屈荷重Pは P=31.4N(=3.2kg重)、下腿部の座屈荷重Pは P=2.89N(=0.3kg重)となり、両脚では600gになりました。
3gのバッタが1mの高さの高さに跳び上がるときに両脚には40gの力がかかりましたが、バッタの脚は細い下腿でも600gの荷重に耐えるので、15倍の安全率です。
なんと自分の体重3gの200倍に耐えられるのです!
○巨大な昆虫の怪獣の運動能力は?
では映画やアニメに出てくるような巨大な昆虫の場合についてみてみます。
上記のバッタがあの形のまま50倍に相似形で大きくになると、体長0.08mx50=4m、 大腿の太さが0.002m×50=10cm、下腿は5cmの太さ、伸ばした脚の長さは4m、体重は50の3乗倍になるので、0.003kg×50x50x50=375kgとなります。
この4mの怪獣が1mの高さまで飛び上がったり、その後に着地したりするときの衝撃力は前と同じ様に計算すると
F=mgh/L m=375kg ,h=5m,L=4m, を代入して
F=4594N(=約469kg重) になります
座屈荷重Pは50の2乗倍になるので P=2.9N×50x50=7250N(=740kg重)
となります。二本脚で約1480kgです。ジャンプの時の脚の強度の安全率は
1480÷469=3.2 と3倍ほどに低下してしまいます。
また、4mの高さにジャンプする時の衝撃はh=8mより、750Kg になるので、片足だと折れ曲がってしまうことになります。これでは、走ったりジャンプしたりしながら戦うことはできそうもありません。
ちなみに100倍になると 体長8m、体重3000kgになり、座屈荷重は2900kg重なので片脚で立つと折れてしまうので、歩くこともできなくなります。
こうしてみると、巨大な怪獣になるにはバッタのようにスマートな体型の外骨格では無理で、クチクラを分厚くして、太めの体型にならないと難しいようです。

(材料工学には素人なので、適切な評価方法のために色々勉強していたので、時間がかかってしまいました。 評価方法に誤りがあればご指摘ください。)
参考文献
1小峯龍男 ゼロからわかる材料力学 技術評論社 東京 2020
2高久田和夫 生体組織の力学-序説 download 2023/11/7
http://www.jsdp.org/kaobio/journal/11/11-1.pdf
3田中英一 皮質骨の力学特性と損傷のモデル化 マテリア 46:460-63 2007
4高嶋聰 クチクラに基づく材料設計論 download 2023/11/10
https://invbrain.neuroinf.jp/modules/htmldocs/IVBPF/Engineering
/Insect_kutikura.html?ml_lang=ja
5「押しつぶされない」コブゴミムシダマシの秘密 download 2023/11/10 Nature2020/10/22https://www.natureasia.com/ja-jp/nature/pr-highlights/13485
6本川達夫 ゾウの時間ネズミの時間 中公新書 1992
7松香光夫ほか 昆虫の生物学 第2版 玉川大学出版 1992
8Wikipediaより バッタの図
9AmvitionのYouTube動画より昆虫怪獣カマキラスの画像download 2023/12/20 https://www.youtube.com/watch?v=_Er4Mtsd9x8










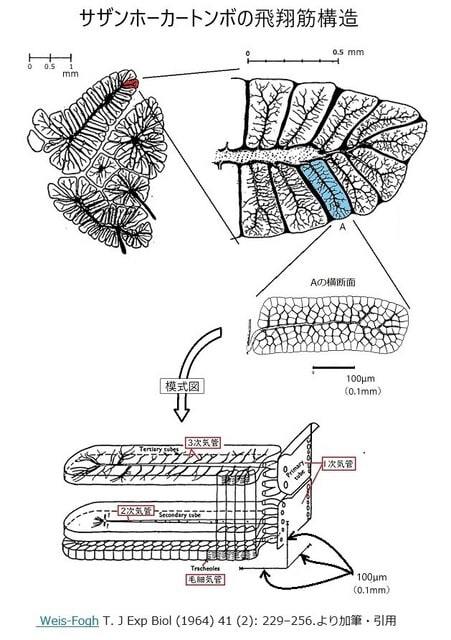
 前回に述べたように、その筋肉(飛翔筋:横紋筋)は安静時に筋肉1g当たり、毎分約 0.02 mlの酸素を消費し、飛行中はその100 倍の毎分 1.5 ~ 3 mlが必要となり、ハチやハエなどは安静時の400倍の毎分8mlと大量の酸素を消費して飛んでいます。
前回に述べたように、その筋肉(飛翔筋:横紋筋)は安静時に筋肉1g当たり、毎分約 0.02 mlの酸素を消費し、飛行中はその100 倍の毎分 1.5 ~ 3 mlが必要となり、ハチやハエなどは安静時の400倍の毎分8mlと大量の酸素を消費して飛んでいます。