ややこしや ～ 線分の比 と 面積の比 ～

まず、図をみてましょう～

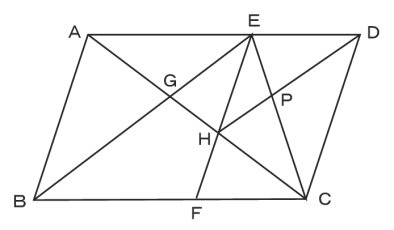
平行四辺形ABCDの 辺AB と辺EF は平行です。

辺AE：辺ED＝３：２ のとき

四角形GBFHと三角形PHCの面積比は、何：何 となるでしょう？

 

 

ヒント：たとえば、△ABC と △HFC は、相似で 線の比は、（３＋２）：２ です。

       面積比は、その２乗ですから、２５：４ となります。

       全体の平行四辺形を １ とした場合の、各部分の面積を考えましょう～

       △ABEだと、平行四辺形ABFEの半分ですね、

      平行四辺形ABFEは、全体の５分の３です。

 

コツが分かれば、計算は単純な作業です。

 

この問題が、すぐに分かっちゃった中学生は

入試対策万全です！

全然わかんない～ という人も、まだ時間はあります。

この図形のすべての部分は、面積比が計算できます。

それらが全部分かれば、この問題と同じ種類の問題は

ほぼ解けます！

こうやって考えればいいのか～ということを、

分かろうとするのか   あきらめるのか   

自分の未来を決めるのは

あなたです。