10は、20の何倍？

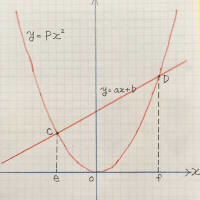
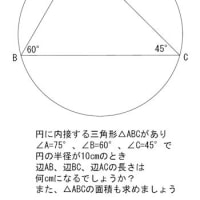
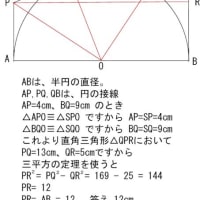
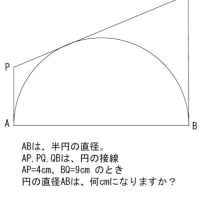
小学校での初めての割り算は、一桁で

６÷３＝   とか    ８÷２＝  とか

左側に右側より大きな数字が出てくるタイプでした。

これは、２桁の計算になっても同じで

左側の数字の方が大きかった！

だから割り算というのは大きな数を小さな数で割るもんだと思ってた。

ところが、

割合というものを習うころより、事情が変わってきます。

-------------------------------------------------

A君はボールを２０個持っていました、

B君は同じボールを１０個持っていました。

B君は、A君の何倍のボールを持っているでしょう。

-------------------------------------------------

このような問題の場合、

式を２０÷１０＝２  と書く子供達が多いのです。

これは、今までずーと大きな数を小さな数で割るという作業をしてきましたから

このように考えるのは、無理のないことで、

これを、間違ってるぞ！と一蹴りすることは無責任。

では、どうすればいいのか？という説明が必要です。

たとえば、絵に描くと

 

と、した場合。まるでB君の体重がA君の体重の何倍あるのか？みたいに見えます。

（見えないかもしれないけど、まあ、分かりにくいと言うことです）

そこで

 

としますと、少し分かりやすい。    かな？

で、もう少し本質をあらわしますと

 

と、なります。そうしますと、ここでていねいに説明して、

ピンクと緑をかけて、黄色になるでしょう？

その時のピンクは、どうやって計算したら分かるでしょう？

たとえば、６＝２×３ の 「３」が、分からない場合と同じです。

かけ算の答えの６を２で割れば３って分かるんだよね。

では、元に戻ってこの３色のカードを並びかえると

と、こんな風になるんだけど

分かりますか？

（ここで、割り算と分数と小数の関係についても確認します。チャンスです）

小さな数を大きな数で割ることもできるんですよ。

算数の世界では、

そんなことはできっこない！と思ってることも

別の世界ではできることがあるんですよ！