ABSTRACT。
水星の近日点運動の43秒角 / 100年の誤差は、ニュートンの力のつり合い式から厳密解が出てきます。 遠心力と万有引力のつり合い式は、GM☉ mg / r² = mi・v² / r。 「絶対静止基準系 + ニュートン力学」の近似解は、v² = GM☉ / r。「2乗3乗の法則 + ニュートン力学」の厳密解にはスケールファクターγが入ります、γ・v² = GM☉ / r。
INTRODUCTION.
アインシュタイン選集(2): [A4]: 水星の近日点の移動に対する一般相対性理論による説明(1915年)
1つ前の[A3]の論文で一般相対性理論はひとまず完成したのだが、その最後の部分で触れられている「水星の近日点の移動」について、具体的な計算をしてみせているのがこの[A4]の論文である。発表年としては[A3]よりも1年前の論文だ。
ご存知のとおり惑星は太陽を1つの焦点においた楕円軌道上を運動する。太陽のまわりには複数の惑星が公転しているので、実際には惑星どうしの重力の影響で、それぞれの惑星が描く楕円軌道の近日点は移動してしまい、この楕円軌道自体の回転のことを天文学では「歳差運動」と呼んでいる。この現象はアインシュタイン以前のニュートン力学でも計算されていたことであった。しかし、実際の観測と理論的な計算結果との間にはわずかなずれがあることが、ルヴェリエという天文学者によって指摘されていた。そのわずかなずれの理論的な説明が一般相対性理論によってなされたわけである。蛇足的であるが、アインシュタインが取り扱ったのは太陽と1つの惑星で構成される「2体問題」における歳差運動の微小なずれである。
MATERIALS AND METHODS.
月の自由落下から発想したニュートン力学の遠心力と万有引力のつり合い式から、
GM☉ mg / r² - mi・v² / r = 0 (1)。
しかしながらニュートン力学(遠隔作用)はケプラーの法則(近接作用)からきているので、重量質量は万有引力定数を係数として体積に比例し、力の比例定数である慣性質量は面積に比例するというのを、言い換えればガリレオの等価原理(物体は重さに関係なく同じ速度で落ちる)なので、
また一般に、スケールの異なる物体や系(システム)を比較する際には、無次元量の整合も求められる場合がある。たとえば、レイノルズ数は代表長さによって値が変わり、これも抗力や揚力に影響する可能性がある
質量等価( mg = mi )は( v ≪ c )の場合の低速近似であり、運動する物体には( mg ≠ mi )の厳密解がある。
そのため、力の定義としては、プランクが指摘したようにニュートンの最初の定義“運動量の時間的変化が力に比例する”に返るべきです。そして、“運動量は慣性質量と速度の積である”とすれば、慣性質量がその運動方向によって異なる非対称的な不条理も無くなる。この形が相対論的に適切な形でしょう。 このように考えれば別稿「アインシュタインの特殊相対性理論(1905年)」3.(5)[補足説明4]で説明した様にγmが“慣性質量”であると考えねばならない。
γ = mi / mg = c / w = c / √( c² ± v² ) (2)。
(式2)の光速度( c )の基準系を無限遠において、(式1)から水星の質量を消去すると、
4 π² γ = GM☉ T² / r³ (4)。
ある惑星の公転周期 P と軌道長半径 a を使ってケプラーの第3法則より日心重力定数は GM☉ = (2π/P)2a3 として容易に計算することができる。
(式4)の左辺の無次元のスケールファクターから公転する一周の差は、
⊿φ = 4 π² ( γー1 ) (5)。
この係数 4π は全周の立体角に由来しており、点電荷の帯びる電気量が、有理系では全周の電束に等しく、非有理系では立体角あたりの電束に等しい。角度が無次元量であるとするならば、電磁気的な量の次元には影響しない。
(式5)を秒角にすると、
"x = ⊿φ ( 180/π )*3600 (6)。
Lookang many thanks to author of original simulation = Todd K. Timberlake author of Easy Java Simulation = Francisco Esquembre - 投稿者自身による作品、CC 表示-継承 3.0、リンクによる。
水星は 88 日で太陽の周りを一周するのだから、100 年で約 415 回転してきたことになるので415周回の秒角は、
"y = 4 π ( γー1 )*180*3600*415 (7)。
離心率にこだわる方はニュートン力学から求めた( v² )へ、
v² = GM☉ / r = GM☉ ( 1 - e² ) / l (8)、
など入れて計算してみるとよい。
ところが、その近日点移動の早さの評価で、「間違っている」とまでは言えないまでも、不整合と言うかわかりにくいと言うか、やはりおかしいところがありましたので、ここで解説したいと思います。
RESULTS AND DISCUSSION。
一般相対性理論でこの誤差を求めるためのパラメータは、「絶対静止基準系 + ニュートン力学」の近似解を利用しているだけで、シュワルトシルト解や測地線方程式は難しくするだけで無用です。
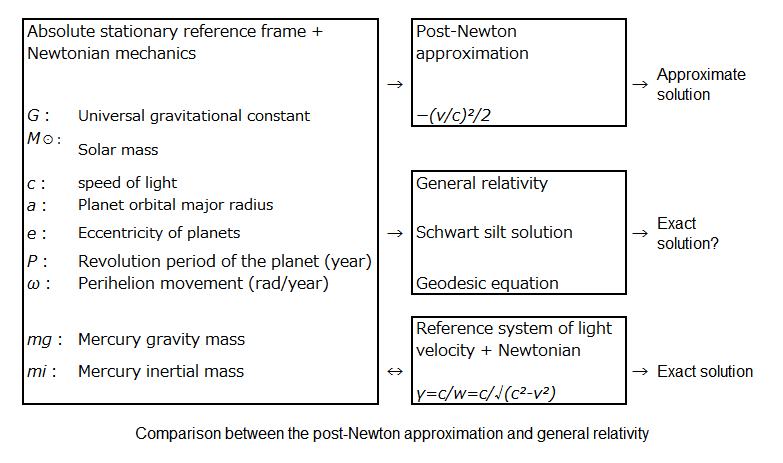
それらから求まる平均軌道速度( v )さえあれば、 光の等価原理(式2)によって、 光速度( c )と平均波動スピード( w )の比( γ )から水星の公転運動の厳密解が求まる。

CONCLUSION。
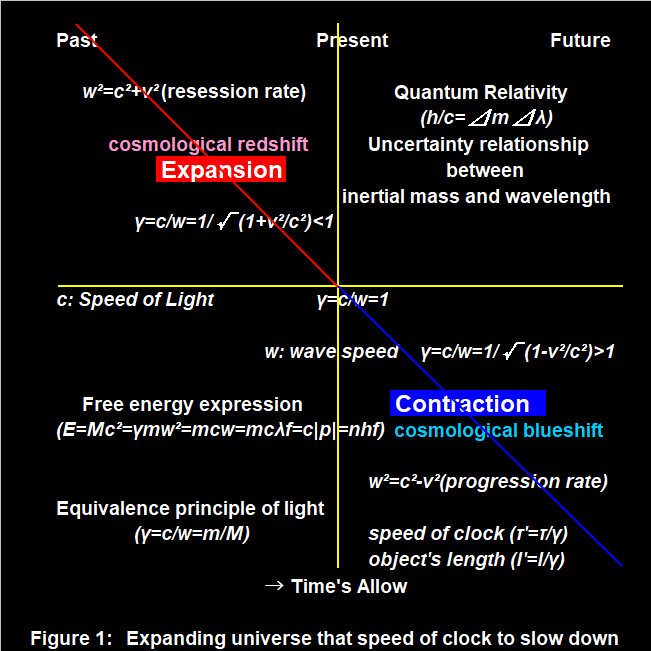
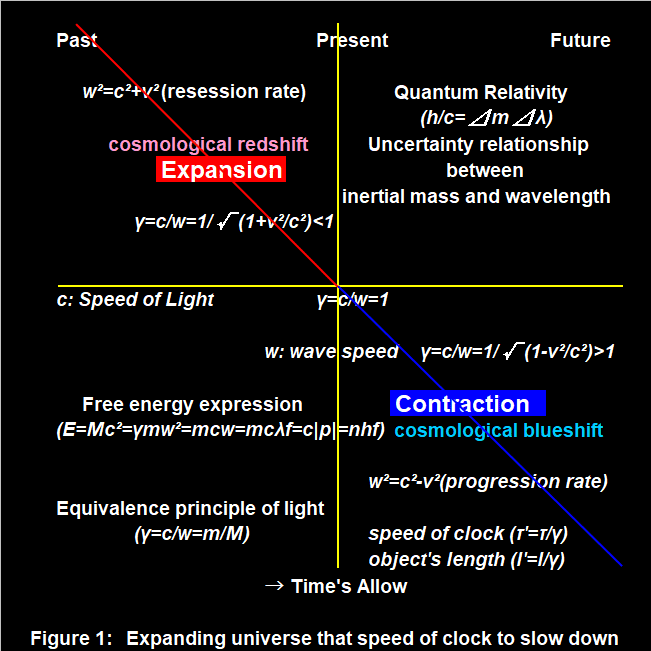
光速度( c ) = 波動スピード( w )、重力質量( mg ) = 慣性質量( mi )になるのは、相対速度( v = 0 )の時だけだ。これは一般相対論が言う局所慣性系から見る視点だ。しかしながらニュートン力学から求める経験値は無限遠を想定した別の視点だ。この観測者の光速度と物体の波動スピードを変換しないで、特殊相対論の光速度不変の観点から「絶対静止基準系+ニュートン力学」の近似( GM/r )へ、この誤差のために2項目を付け足す近似は、ミクロからマクロまでフルスケールでデルタ関数問題を引き起こす。
光の等価原理では先に「光速度の基準系+ニュートン力学」へ変換後、
w²=c²±v²。
観測者( c )から見た運動( v )する物体の波動スピード( w )=物体の時計の進み方に還元し、エネルギーや光の運動量を一項で取り扱うので、一般相対論のデルタ関数問題は生じない。
E = c |p| = h・f = mg・c² = γ・mi・w²。
https://www.youtube.com/watch?v=vdEcpxz8tew
つまり波動スピードと時計の進み方は同じ意味であり、波動スピードと時計の進み方が別々に変化することはない。 無次元のスケールファクターで不変性を原理にして縛っても、階層性問題がフルスケールで発生させるだけで力学にはならないでしょう。
Acknowledgment。
5chに寄生して反論してくれた皆様のおかげで、本論の見通しが良くなったことに感謝する。
Appendix。
1、GPS衛星に搭載された原子時計の、相対論による一般相対論効果+ポストニュートン近似の特殊相対論的効果は、
GPS 衛星上では相対論的効果により、時間の進み方が地表と異なるので、 あらかじめ衛星搭載時計の周波数を(-4.45e-10)オフセットして、UTC(協定世界時)と同期し ています。
一般相対論による補正(重力による赤方偏移)地球表面と、GPS 衛星上での重力ポテンシャルの差により、GPS衛星上での時間は地表より早く進みます。その大きさは、。
特殊相対論による補正(2次ドップラー効果)GPS 衛星の速度(3.874 km/sec)により、GPS 衛星上での時間は地表より遅くなります。その大きさは、。
地表の光速度( c ) : 299,792,458 m/s。
地心重力定数( GM ) : 3.986e + 14 m³/s²。
地球半径( r ) : 6,378,000 m。
双曲線無限の波動スピード、 w∞ = √( c² + 2GM / r )。
GPS衛星の高度( h ) : 20,200,000 m。
GPS衛星の軌道速度( v ) : 3,874 m / s。
GPS衛星の波動スピード、 wg = √( w∞² - 2GM /( r + h ) - v² )。
時計の進み方の違い、 wg / c = 1 + 4.45e-10。