ここでは「時間と光速を別々に取り扱う間違い」が、ローレンツ変換にある理由を説明する。
- 1、光速が一定な理由
- 2、ローレンツの間違い
- 3、アインシュタインの間違い
- 4、同じ慣性系の真空中の光速は一定
- 5、異なる慣性系間の光速の変化
- 6、観測者が運動する場合の速度合成
- 7、ローレンツ変換とは?
波動現象において、周期を T [s] とすると、波の周波数 f [Hz] は次のように定義される。
f₀ = 1 / T₀ (Hz) (1).
この周期( T₀ )を波長( λ₀ )に変えると、真空中の光速度( c )になる。
f₀ = c / λ₀ (Hz) (2).
|
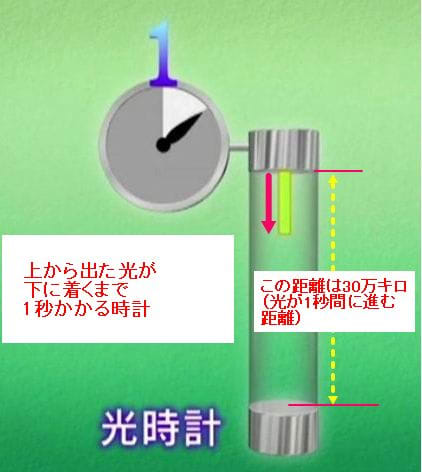
この時間スケール( 1 )が変化するということは、( c )も変化するということである。 これは光時計( c )であろうが置時計( 1 )であろうが、時計には変わりないことから自明である。 したがって、時間が変化する( 1 )ということは光速が変化する( c )ことと同じ意味であり、その比は一定である。 |
|
マイケルソン・モーリーの実験を受け、ローレンツは絶対静止座標系でc±v光速と運動の速度合成がガリレイ変換にならない理由として、物差しが進行方向に収縮する=ローレンツ収縮を考えた。
|
|
したがってそれによりガリレイ変換からローレンツ変換にしたところでそれは間違いである。 |
ローレンツと逆に光速は不変( c )、時間( t )が変化( τ )するとしたのが、アインシュタインの相対性理論である。
(ct)²-x²-y²-z²(c: 光速、t: 観測者にとっての時間、(x, y, z): 観測者にとっての物体の空間座標)はローレンツ変換に関して不変な量である(つまりいかなる座標系で物体を観測してもこの値は同じになる)。そこで、d(cτ)²=d(ct)²-dx²-dy²-dz²としてτ=∫dτとτを定義すると、このτも不変量となる。このτが固有時である。
その座標変換はローレンツ変換をなぜか採用している。
ガリレイ変換からローレンツ変換にしたところで、それも間違いである。
しかもローレンツは、アインシュタインの時間が変化する方が正しいとして、ローレンツ変換で時間が変化することを容認している?
アインシュタインは光速度不変を前提にしているが、慣性系間の光速は一定にならない。
光速度不変の原理の破れ
ローレンツが間違いであれば、アインシュタインも間違いである。
電磁気学の自由空間を絶対静止基準系にすると、全域が光速度で、時計の進み方はどこでも同じになる。
電磁気学において、自由空間(じゆうくうかん、free space)とは一切の物質が存在しない仮想的な空間である。真空中の光速および、真空の透磁率、真空の誘電率といった物理定数により定義される。
電磁気学の自由空間を観測者と同じ慣性系にすると、その慣性系の真空中の光速は一定になる。
この「観測者と同じ慣性系の真空中の光速は一定である」を、光速度の基準系にするということに反対する学者はいないだろう。
ガリレオやニュートンの慣性系は、別に慣性系だけを言ってるのではなく、慣性系と非慣性系の区別、つまり力学的な関係を前提にしている。
その区別がなければ、何が慣性系か非慣性系かの区別もない。
したがって運動する物の時計は遅れるというのは、お互い様ではなく、観測者を加速するのか?それとも対象を加速するのか? によって運動に対する時間の進み方の符号も変わる。
マイケルソン・モーリーの実験で公転する地球の観測者の場合と、観測者と観測対象の両方が運動する場合の速度合成の仕方は、
マクスウェルの方程式も、絶対静止座標系の概念とは無関係である。
またニュートン力学も、
ニュートン力学では、宇宙における絶対静止座標系が存在しないので、あらゆる速度は常にその時々の観測者から見た相対速度である。
以上の古典論が絶対静止基準系だけで成り立つとしてローレンツ変換が考えられた。 しかし古典論がそれに縛られないなら、そもそも無用だったという話だ。













※コメント投稿者のブログIDはブログ作成者のみに通知されます